CASIO

Ví dụ 1: (1, 2) + (3, 4) (cộng véc-tơ)

Nhấn , chọn biểu tượng phương thức Vector, rồi sau đó nhấn .

• (VctA)(2 chiều)
  12
• 

• 
• 

• (Define Vector)
• 

• (VctB)(2 chiều)
  34
• 

• 
• 

• Màn hình tính toán véc-tơ

VctA + VctB:

• (VctA)(VctB)
• 

• 
• 

Thao tác này sẽ hiển thị màn hình VctAns (Bộ nhớ trả lời véc-tơ) với kết quả tính toán.

Ví dụ 2: Để sao chép VctA = (1, 2) vào VctB và chỉnh sửa nội dung của VctB thành VctB = (3, 4)

• (Edit Vector)
• 

• (VctA)
• 

• (VctB)
• 

• 34
• 

Ví dụ sau đây dùng VctA = (1, 2), VctB = (3, 4), VctC = (2, -1, 2).

Ví dụ 3: 3 × VctA (Nhân vô hướng véc-tơ), VctB － 3 × VctA (Ví dụ tính toán dùng VctAns)

• 3(VctA)
• 

• 
• 

• (VctB)(VctAns)
• 

• 
• 

Ví dụ 4: 3 × VctA (Nhân vô hướng véc-tơ)

• (VctA)
• 

• 
• 

Ví dụ 5: VctA • VctB (Dấu chấm nhân véc-tơ)

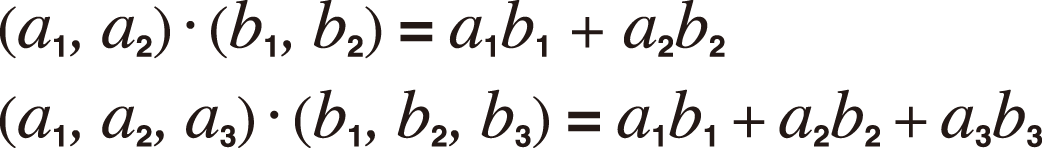
• (VctA)(Dot Product)
  (VctB)
• 

Ví dụ 6: VctA × VctB (Dấu nhân véc-tơ)

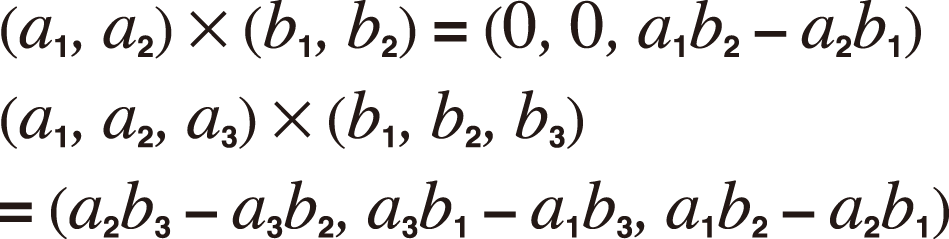
• (VctA)(VctB)
• 

• 
• 

Ví dụ 7: Để thu được độ lớn của VctC (Abs(VctC))

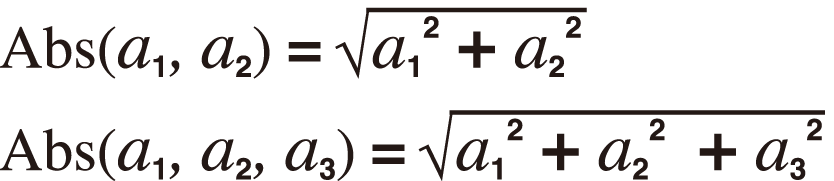
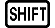
• (Abs)(VctC)
• 

Ví dụ 8: Để xác định góc được tạo nên bởi VctA và VctB (Angle(VctA,VctB)) theo ba vị trí thập phân (Fix 3). (Angle Unit: Degree)

• (Angle)(VctA)
  (,)(VctB)
• 

Ví dụ 9: Để chuẩn hóa VctB (UnitV(VctB))

• (Unit Vector)
  (VctB)
• 

• 
• 

Ví dụ 10: Để xác định kích thước của góc được tạo nên bởi vec-tơ A = (-1, 0, 1) và B = (1, 2, 0) và một trong các kích thước của 1 vec-tơ vuông góc với cả A và B. (Angle Unit: Degree)

• (Define Vector)(VctA)
  (3 chiều)
  101
• 

• (Define Vector)(VctB)
  (3 chiều)
  120
• 

VctA • VctB:

• (VctA)(Dot Product)
  (VctB)
• 

Ans ÷ (Abs(VctA) × Abs(VctB)):

• (Abs)(VctA)
  (Abs)(VctB)
• 

cos-1 Ans ^*1:

• (cos-1)
• 

VctA × VctB:

• (VctA)(VctB)
• 

Abs(VctAns):

• (Abs)(VctAns)
• 

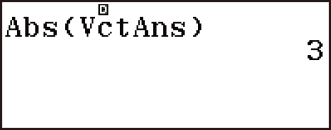
VctAns ÷ Ans *2:

• (VctAns)
• 

*1 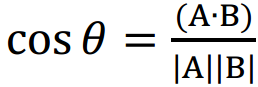, mà trở thành .

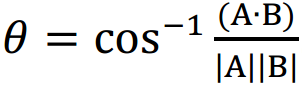*2 Kích thước của 1 vector vuông góc với cả A và B 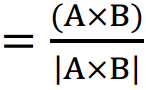.