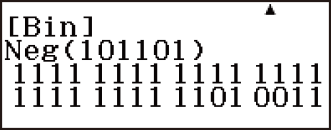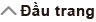Tính toán cơ số n
Phép toán logic và phủ định
Phép toán logic và phủ định được thực hiện bằng cách nhấn 
.
| Khi bạn muốn nhập: | Thực hiện thao tác phím này: |
|---|---|
| Hàm “Neg(”, trả về kết quả bù của hai |  (Neg) |
| Hàm “Not(”, trả về kết quả bù theo bit |  (Not) |
| Toán tử logic “and” (tích logic), trả về kết quả AND theo bit |  (and) |
| Toán tử logic “or” (tổng logic), trả về kết quả OR theo bit |  (or) |
| Toán tử logic “xor” (tổng logic loại trừ), trả về kết quả XOR theo bit |  (xor) |
| Toán tử logic “xnor” (tổng logic âm loại trừ), trả về kết quả XNOR theo bit |  (xnor) |
Lưu ý
Trong trường hợp giá trị nhị phân, bát phân hoặc thập lục phân âm, máy tính chuyển đổi giá trị này sang nhị phân, lấy phần bù của hai và sau đó chuyển ngược về phương thức số gốc. Với giá trị thập phân, máy tính tay đơn thuần thêm dấu trừ.
Ví dụ
Tất cả những ví dụ sau đều được thực hiện trong phương thức nhị phân (
(BIN)).
Ví dụ 1: Để xác định phép và logic AND của 10102 và 11002 (10102 and 11002)
1010(and) 1100
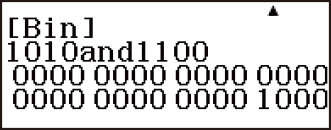
Ví dụ 2: Để xác định phép logic OR của 10112 và 110102 (10112 or 110102)
- 1011(or) 11010
Ví dụ 3: Để xác định phép logic XOR của 10102 và 11002 (10102 xor 11002)
- 1010(xor) 1100
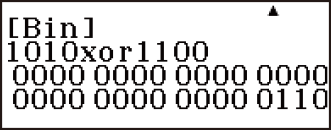
Ví dụ 4: Để xác định phép logic XNOR của 11112 và 1012 (11112 xnor 1012)
- 1111(xnor) 101
Ví dụ 5: Để xác định phần bù theo bit của 10102 (Not(10102))
- (Not) 1010
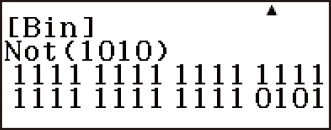
Ví dụ 6: Để phủ định (lấy phần bù của hai) của 1011012 (Neg(1011012))
- (Neg) 101101
