Detalles del menú Catalog
El menú Catalog, que aparece al presionar C, incluye una lista exhaustiva con todas las funciones, los comandos, las variables de las aplicaciones* y los símbolos disponibles en la calculadora. Puede seleccionar el elemento que desee en la calculadora e introducirlo en un cálculo o una expresión.

La lista que se genera mediante C > [All] contiene todos los elementos admitidos por la calculadora. Mientras se muestre la lista ordenada alfabéticamente, puede presionar cualquier tecla de la XA a la 0Z para visualizar una lista de elementos que empiecen por esa letra.
Puede acceder a las funciones y los símbolos que no se incluyan en un grupo de la [A] a la [Z] mediante C > [All] > [Symbol].
Elementos incluidos en C > [Variable Data] (variables de entrada/salida utilizadas en una aplicación)
Nota
Si presiona C cuando está utilizando las aplicaciones Python o Base-N, se mostrará el menú Catalog específico de cada aplicación. Para obtener detalles, consulte los apartados que explican el funcionamiento de cada aplicación.
En el menú Catalog se muestran los nombres de las funciones y los comandos de los menús por categoría (como Integration (∫), etc.). En los menús C > [All] y de historial de introducción, la sintaxis de las funciones y los comandos se muestra en forma de línea (∫(,,), etc.).
Uso del historial de introducción
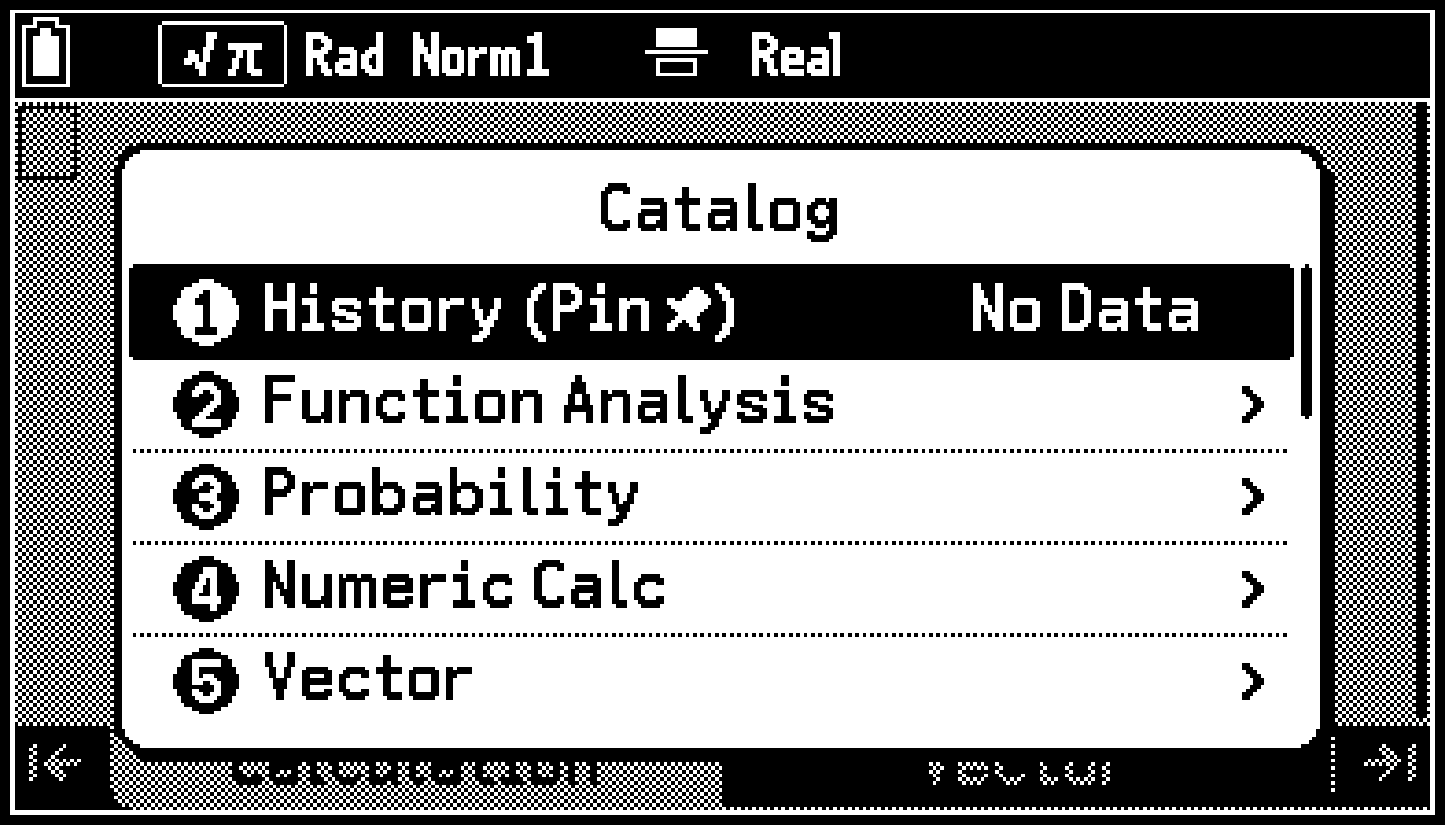
Se conservan como historial de introducción hasta los 10 últimos comandos y funciones* introducidos desde el menú Catalog. Para visualizar el historial de introducción, seleccione C > [History (Pin ![]() )].
)].
Incluido el historial de introducción anclado.
Anclar el historial de introducción
En el historial de introducción, seleccione el elemento que desee anclar y, a continuación, presione T. Se mostrará un icono de chincheta a la izquierda del elemento.
La próxima vez que abra el historial de introducción, el elemento anclado se mostrará en la parte superior de la lista.
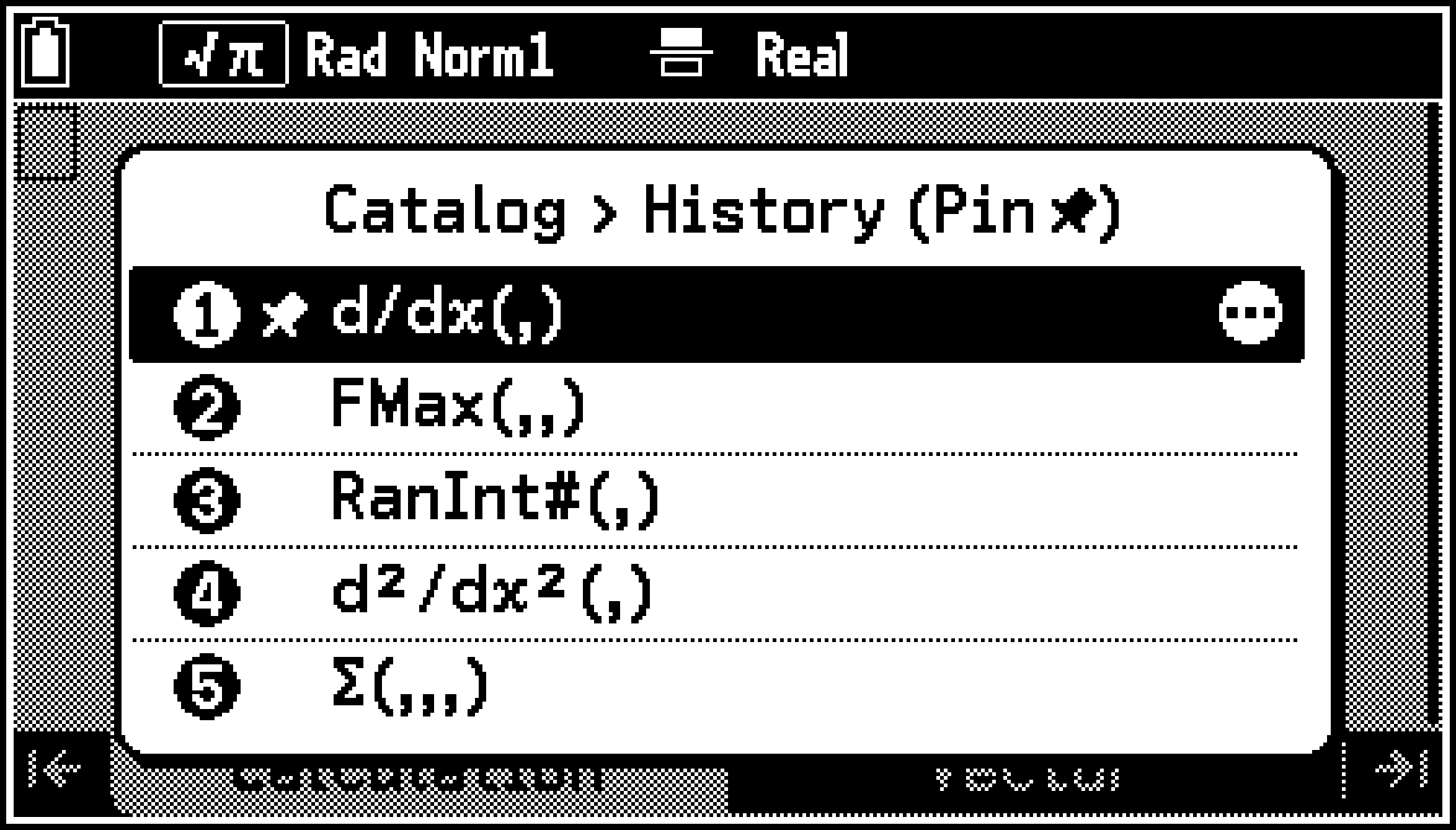
Para dejar de anclar un elemento, seleccione el elemento que desee dejar de anclar y presione T.
Lista de elementos agrupados por categoría
Tenga en cuenta los siguientes puntos relativos a la sintaxis de las funciones y los comandos, excepto para los de la categoría Unit Conversions.
Si la sintaxis de introducción natural y la que se expresa en forma de línea son diferentes para una función, se mostrará primero la de introducción natural, seguida de la otra.
Los elementos opcionales de la sintaxis se muestran entre corchetes ([ ]). En el ejemplo de sintaxis , el argumento puede omitirse, lo que da como resultado .
Nota
Las categorías enumeradas en esta sección y las funciones, los comandos, las variables de las aplicaciones* y los símbolos incluidos en cada categoría se presentan en el orden en que aparecen cuando se selecciona [Country] > [International] en la aplicación System.
Independientemente del modelo (fx-CG100 o fx-1AU GRAPH) o la configuración, los elementos incluidos en C > [All] no varían. Todos los elementos enumerados en esta manual se muestran en orden alfabético.
Elementos incluidos en C > [Variable Data] (variables de entrada/salida utilizadas en una aplicación)
Function Analysis
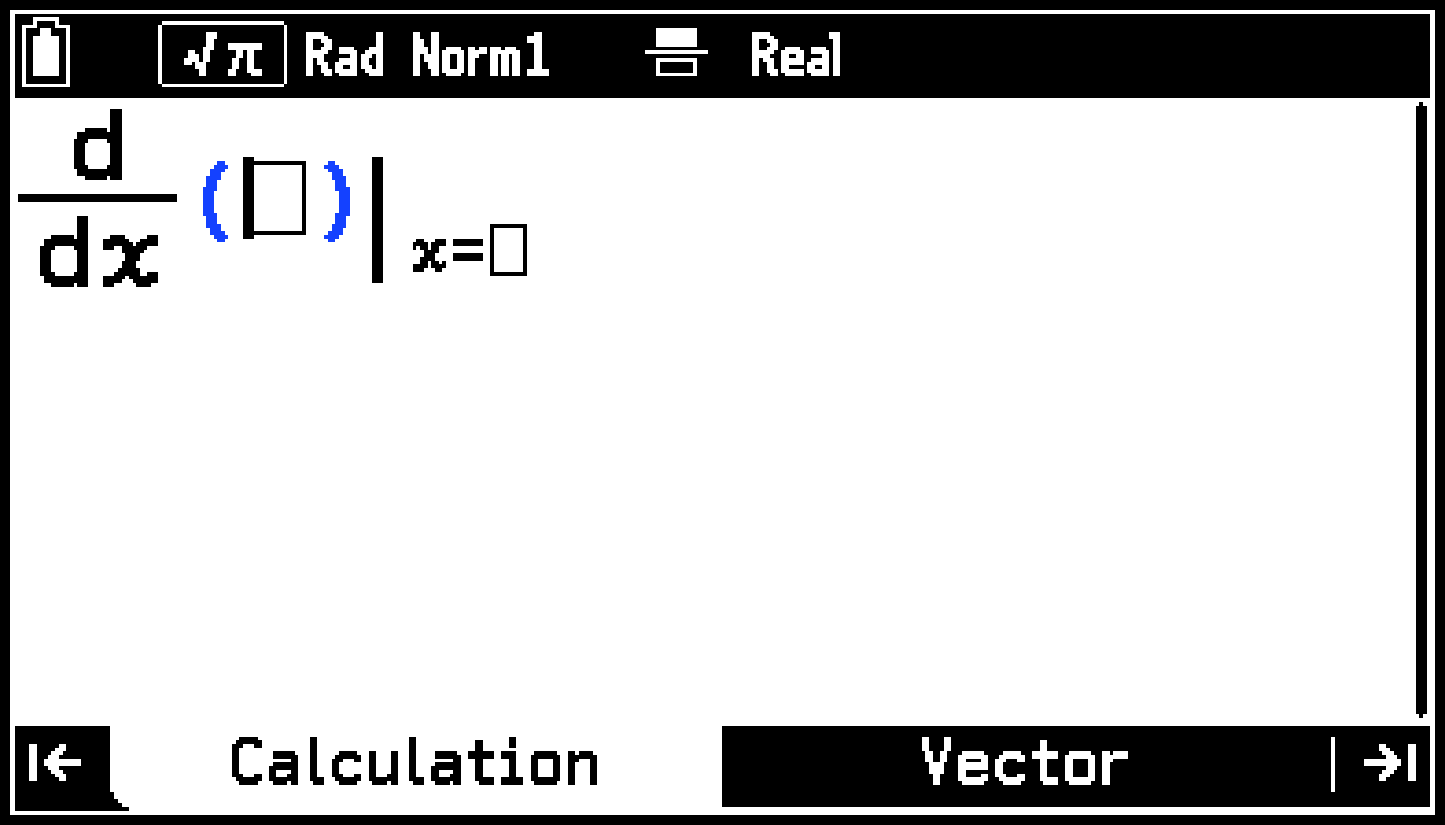
1st Derivative (d/dx) d/dx(,)
Emplea el cálculo aproximado para determinar el coeficiente diferencial de primer orden de en .
Sintaxis:
Elementos no permitidos en esta sintaxis: , , , Σ, FMin, FMax, Solve, RndFix
Ejemplo:
Precauciones
Cuando sea una función trigonométrica, asegúrese de seleccionar lo siguiente para la unidad de ángulo: S > [Angle] > [Radian].
Lo siguiente puede generar errores o resultados imprecisos:
Puntos discontinuos en valores
Cambios extremos en valores
Inclusión de un punto mínimo local y un punto máximo local en valores
Inclusión de un punto de inflexión en valores
Inclusión de puntos indiferenciables en valores
Resultados de cálculo cercanos a cero
2nd Derivative (d2/dx2) d2/dx2(,)
Emplea el cálculo aproximado para determinar el coeficiente diferencial de segundo orden de en .
Sintaxis:
Las precauciones y los elementos que no están permitidos en esta sintaxis son los mismos que para .
Integration (∫) ∫(,,)
Emplea el cálculo aproximado para determinar la integral de en ≤ ≤ . Esta función devuelve un valor positivo cuando está en un rango positivo, y un valor negativo cuando está en un rango negativo (ejemplo: ; ).
Sintaxis:
Para , introduzca el rango (de tolerancia) de error permisible. Ajuste predeterminado: 1 × 10-5 si se omite y para introducción natural.
Elementos no permitidos en esta sintaxis: , , , Σ, FMin, FMax, Solve, RndFix
Ejemplo:
Precauciones
Cuando sea una función trigonométrica, asegúrese de seleccionar lo siguiente para la unidad de ángulo: S > [Angle] > [Radian].
Dado que se utiliza la integración numérica, puede producirse un error importante en los valores de integración calculados debido al contenido de , los valores positivos y negativos del intervalo de integración o el intervalo que se está integrando. (Ejemplos: Cuando hay partes con puntos discontinuos o cambios abruptos, o cuando el intervalo de integración es demasiado amplio). En dichos casos, dividir el intervalo de integración en varias partes antes de realizar los cálculos puede mejorar la precisión de cálculo.
Summation (Σ) Σ(,,,)
Obtiene la suma para un rango especificado de .
Sintaxis: , , = enteros, <
puede ser cualquier variable alfabética. especifica el intervalo escalonado. Ajuste predeterminado: 1 si se omite y para introducción natural.
Elementos no permitidos en esta sintaxis: , , , Σ, FMin, FMax, Solve, RndFix
Ejemplo:
Solve Equation (SolveN) SolveN()
Obtiene varias soluciones de una ecuación.
Sintaxis: SolveN( [= lado derecho] [,] [,límite inferior,límite superior])
Si se omite [=lado derecho], se asume que = 0. Especifique cualquier variable alfabética para [] y use la misma variable para . Si se omite [,], se usa la variable .
Se devuelven hasta 10 soluciones en forma de lista.
Se devuelve “No Solution” si no existen soluciones.
Si puede que existan más soluciones aparte de las proporcionadas, se muestra el mensaje “More solutions may exist.” en la pantalla.
Elementos no permitidos en esta sintaxis: , Σ, FMin, FMax, Solve
Ejemplo: SolveN
Solve Equation (Solve) Solve(,)
Se aproxima a una solución única para = 0. Esta función tiene el mismo uso que Uso de la función Solver de la aplicación Equation.
Sintaxis: Solve( ,estimación inicial [,límite inferior,límite superior])
Elementos no permitidos en esta sintaxis: , Σ, FMin, FMax, Solve
Remainder of Integer÷Integer Rmdr
Obtiene el resto cuando un entero se divide por otro entero.
Sintaxis: dividendo Rmdr divisor
Ejemplo: 17 Rmdr 7 = 3
Integer Part of Int÷Int Int÷
Obtiene el cociente cuando un entero se divide por otro entero.
Sintaxis: dividendo Int÷ divisor
Ejemplo: 17 Int÷ 7 = 2
Simplification ISimp
Reduce una fracción a sus términos menores. Utilice la siguiente configuración con la aplicación Calculate.
S > [Simplify] > [Manual]
S > [Complex Mode] > [Real]
Utilice una de estas sintaxis para ISimp.
Sintaxis 1: FracciónISimp
Reduce automáticamente la fracción del argumento dividiendo por el número primo menor por el que puede dividirse. El número primo y el resultado de la reducción se muestran en pantalla.
Sintaxis 2: FracciónISimp
Divide la fracción del argumento por el divisor especificado por . El resultado de la división se muestra en pantalla.
Ejemplo 1:
15e60r
C > [Function Analysis] > [Simplification]E

C > [History (Pin ![]() )] > [ISimp]E
)] > [ISimp]E

Ejemplo 2: (especifica un divisor de 5)
15e60r
C > [Function Analysis] > [Simplification]5E

Precauciones
Cuando se selecciona [a+b] o [r∠θ] para S > [Complex Mode], los resultados de cálculo de la fracción siempre se simplifican antes de mostrarse, incluso si S > [Simplify] está ajustado en [Manual].
Function Minimum FMin(,,)
Devuelve, en forma de lista, las coordenadas de los valores mínimos de en ≤ ≤ .
Sintaxis: FMin(,,[,]) : precisión de cálculo ( = entero del 1 al 9)
Elementos no permitidos en esta sintaxis: , , , Σ, FMin, FMax, Solve, RndFix
Ejemplo: FMin(,-2,1) = {0,0}
Precauciones
Las secciones o los puntos discontinuos con una fluctuación drástica pueden afectar negativamente a la precisión o provocar un error.
Si introduce un valor mayor para aumentará la precisión de cálculo, pero también la cantidad de tiempo requerido para realizar el cálculo.
Function Maximum FMax(,,)
Devuelve, en forma de lista, las coordenadas de los valores máximos de en ≤ ≤ .
Sintaxis: FMax(,,[,]) : precisión de cálculo ( = entero del 1 al 9)
Las precauciones y los elementos que no están permitidos en esta sintaxis son los mismos que para FMin.
Probability
Factorial (!) !
Obtiene el factorial de 0 o un entero positivo.
Sintaxis: = entero
Permutation (P) P
Obtiene el número total de permutaciones tomadas del valor establecido.
Sintaxis: P , = enteros
Combination (C) C
Obtiene el número total de combinaciones del valor establecido.
Sintaxis: C , = enteros
Random Number (0 to 1) Ran#
Cada ejecución devuelve un número aleatorio de 10 dígitos (del 0 al 1).
Sintaxis: Ran# [] 1 ≤ ≤ 9 ( = entero)
: Especifica la secuencia de números aleatorios. Si se omite, se devuelve un número aleatorio verdadero. Si se especifica, se invoca la secuencia de números aleatorios de la calculadora correspondiente y se devuelve un número aleatorio fijo. Por ejemplo, ejecutar Ran# 1 después de inicializar las secuencias* siempre devuelve números aleatorios de la Secuencia 1 en orden (0,701320948, 0,9297706456, 0,2939058016...).
Para inicializar las secuencias, ejecute Ran# 0. Esto también inicializa las secuencias de RanList#. Las secuencias también pueden inicializarse utilizando Ran# o RanList# para generar una serie de números aleatorios diferente de la última serie ejecutada o generando un número aleatorio verdadero.
Random Integer (n to m) RanInt#(,)
Genera un número aleatorio entero entre dos enteros especificados y .
Sintaxis: RanInt#(,[,]) < , || < 1×1010, || < 1×1010, ‒ < 1×1010, 1 ≤ ≤ 999
: Especifica el total de números aleatorios. Si se omite, se devuelve un número aleatorio. Si se especifica, devuelve el total especificado de números aleatorios en forma de lista.
Random Number (Normal) RanNorm#(,)
Aplica la distribución normal para generar un número aleatorio de 10 dígitos basado en la media especificada y la desviación estándar .
Sintaxis: RanNorm#(,[,]) > 0, 1 ≤ ≤ 999
: especifica el total de números aleatorios. Si se omite, se devuelve un número aleatorio. Si se especifica, devuelve el total especificado de números aleatorios en forma de lista.
Ejemplo: Generar un número aleatorio de valores de altura obtenidos de acuerdo con una distribución normal para un grupo de niños de menos de un año con una altura media de 68 cm. Asumiremos que la desviación estándar es 8: RanNorm#(8,68)
Random Number (Binomial) RanBin#(,)
Utiliza la distribución binomial basada en el número especificado de intentos y el valor de probabilidad para generar un entero aleatorio.
Sintaxis: RanBin#(,[,]) 1 ≤ ≤ 100000, 1 ≤ ≤ 999, 0 ≤ ≤ 1
: especifica el total de números aleatorios. Si se omite, se devuelve un número aleatorio. Si se especifica, devuelve el total especificado de números aleatorios en forma de lista.
Random Num (0 to 1) to List RanList#()
Cada ejecución devuelve, en forma de lista, el total especificado de números aleatorios (del 0 al 1, 10 dígitos).
Sintaxis: RanList#([,]) 1 ≤ ≤ 9, 1 ≤ ≤ 999 (, = enteros)
: Especifica el número de intentos. Este parámetro especifica el total de números aleatorios que van a generarse.
: Igual que Ran#.
Ejemplo: (Inmediatamente después de ejecutar Ran# 0) RanList#(3,1) = {0.701320948,0.9297706456,0.2939058016}
Random Sample from List RanSamp#(,)
Muestrea elementos de una lista de forma aleatoria y devuelve el resultado en forma de lista.
Sintaxis: RanSamp#(List,[,])
List: variables de lista (List 1 a List 26 o List Ans)*, o una lista
Las variables de lista también se pueden especificar mediante subnombres.
: Número de intentos (1 ≤ ≤ 999 cuando = 0, 1 ≤ ≤ número de elementos de List cuando = 1)
: Especifica 0 o 1 (0 cuando se omite). Cuando = 0, cada elemento puede extraerse varias veces. Cuando = 1, cada elemento solo se puede extraer una vez.
Ejemplo:
Extraer dos elementos aleatorios de {1,3,6,7}: RanSamp#({1,3,6,7},2,1)
Extraer cinco elementos aleatorios de {1,3,6,7}: RanSamp#({1,3,6,7},5)
Numeric Calc
GCD GCD(,)
Obtiene el mayor divisor común de varios enteros.
Sintaxis: GCD(,)
LCM LCM(,)
Obtiene el menor múltiplo común de varios enteros.
Sintaxis: LCM(,)
Absolute Value Abs()
Encuentra el valor absoluto del argumento .
Sintaxis: || Abs()
Integer Part Int()
Extrae la parte entera del argumento .
Sintaxis: Int()
Ejemplo: Int(-3.5) = -3
Fraction Part Frac()
Extrae la parte fraccionaria del argumento .
Sintaxis: Frac()
Ejemplo: Frac(-3.5) = -0.5
Round Off Rnd
Esta función está disponible en la pestaña Calculation de la aplicación Calculate. Redondea el valor del último resultado de cálculo (Ans) de la pantalla de resultados de acuerdo con el ajuste S > [Display].
Sintaxis: Rnd (sin argumento y válido solo para resultados de cálculo anteriores)
Ejemplo: Con [Display] > [Fix3: 0.123], dividir 10 por 3 y, a continuación, multiplicar Ans por 3
Sin Rnd:
10*3E
/3E

Con Rnd:
10*3E
C > [Numeric Calc] > [Round Off]E
/3E

Cuando el ajuste establecido es [Display] > [Fix3: 0.123], se muestra 10÷3=3.333, pero internamente se conservan 15 dígitos, por lo que Ans×3=10.000. Si el resultado de 10÷3 se redondea con Rnd como se ha mostrado, Ans×3=9.999.
Largest Integer Intg()
Devuelve el mayor entero que no excede el argumento .
Sintaxis: Intg()
Ejemplo: Intg(-10.56) = -11
Round Internal RndFix()
Redondea el argumento al lugar que sigue al número de decimales especificado por (0 a 9).
Sintaxis: RndFix([,])
Si se omite , el redondeo se lleva a cabo de acuerdo con el ajuste S > [Display], igual que con la función Rnd.
Elementos no permitidos en esta sintaxis: , , , Σ, FMin, FMax, Solve, RndFix, logab
Ejemplo: RndFix(1.23456,3) = 1.235
Division Remainder MOD(,)
Esta función permite obtener el resto de una división. Devuelve el resto cuando se divide por .
Sintaxis: MOD(,) (, = enteros)
Ejemplo: MOD(17,3) = 2
Remainder Exponentiation MOD_Exp(,,)
Esta función calcula exponentes modulares. Devuelve el resto cuando se multiplica por potencia y luego se divide por .
Sintaxis: MOD_Exp(,,) (, , = enteros)
Ejemplo: MOD(2,4,3) = 1
Vector
Vct y Vct pueden ser vectores o variables de vector.
Los vectores del ejemplo (como ) se introducen mediante T > [m×n]. Para obtener más detalles, consulte Introducir un vector en un cálculo.
Nota
Al calcular un producto escalar, un producto cruzado y un ángulo formado por dos vectores, las dimensiones de los dos vectores deben ser las mismas.
Vector Vct
Introduce “Vct ”. A continuación, especifique una variable de vector introduciendo una letra de la A a la Z, o Ans.
Dot Product DotP(,)
Obtiene el producto escalar de dos vectores.
Sintaxis: DotP(Vct ,Vct )
Ejemplo: DotP(,) = 11
Cross Product CrossP(,)
Obtiene el producto vectorial de dos vectores.
Sintaxis: CrossP(Vct ,Vct ) (las dimensiones de Vct y Vct deben ser 1 × 2, 1 × 3, 2 × 1, o 3 × 1).
Ejemplo: CrossP(,) =
2-Vector Angle Angle(,)
Obtiene el ángulo entre dos vectores.
Sintaxis: Angle(Vct ,Vct )
Ejemplo: Cuando S > [Angle] > [Radian], Angle(,) =
Unit Vector UnitV()
Calcula el vector unitario del vector especificado por el argumento.
Sintaxis: UnitV(Vct )
Ejemplo: UnitV() =
Vector Norm Norm()
Calcula la norma (magnitud) de un vector o una matriz especificados.
Sintaxis: Norm(Vct ) ; Norm(Mat ) (Mat = matriz o variable de matriz)
Ejemplo: Norm() = ; Norm() =
Matrix
Mat y Mat son matrices o variables de matriz.
Las matrices del ejemplo (como ) se introducen mediante T > [m×n]. Para obtener más detalles, consulte Introducir una matriz en un cálculo.
Nota
Los determinantes y las matrices inversas están sujetos a errores debidos a la omisión de dígitos.
Puede que la forma escalonada de una matriz y la forma escalonada reducida de una matriz no generen resultados precisos debido a la omisión de dígitos.
Matrix Mat
Introduce “Mat ”. A continuación, introduzca una letra de la A a la Z, o Ans para especificar una variable de matriz.
Inverse Matrix -1
Obtiene la inversa de la matriz cuadrada especificada.
Sintaxis: Mat
Ejemplo: =
Precauciones
La precisión de cálculo se ve afectada para las matrices cuyo determinante se acerca al cero.
Determinant Det()
Obtiene el determinante de la matriz cuadrada especificada.
Sintaxis: Det(Mat )
Ejemplo: Det() = -2
Matrix Transpose Trn()
Obtiene la matriz traspuesta de la matriz especificada.
Sintaxis: Trn(Mat )
Ejemplo: Trn() =
Nota
El comando “Trn” también puede utilizarse con un vector. Convierte un vector de 1 fila × columnas en un vector de filas × 1 columna, o un vector de filas × 1 columna en un vector de 1 fila × columnas.
Matrix Identity Identity()
Crea una matriz identidad con un número específico de filas y columnas.
Sintaxis: Identity() ( = entero)
Ejemplo: Identity(2) =
Row Echelon Form Ref()
Este comando emplea el algoritmo de eliminación de Gauss para encontrar la matriz escalonada de una matriz.
Sintaxis: Ref(Mat )
Ejemplo: Ref() =
Reduced Row Echelon Form Rref()
Obtiene la matriz escalonada reducida de una matriz especificada.
Sintaxis: Rref(Mat )
Ejemplo: Rref() =
Matrix Augment Augment(,)
Combina dos matrices (o vectores), cada una de ellas con el mismo número de filas, en una única matriz.
Sintaxis: Augment(Mat ,Mat ) ; Augment(Vct ,Vct )
Una o las dos matrices (Mat , Mat ) pueden sustituirse por Vct , Vct , respectivamente.
Ejemplo: Augment(,) = ; Augment(,) =
Fill Matrix Fill(,)
Sustituye todos los elementos de una variable de matriz (o una variable de vector) por el valor especificado.
Sintaxis: Fill(,Mat ) ; Fill(,Vct )
Dimensions Dim()
-
Obtiene las dimensiones de una matriz (o de un vector) y las genera en forma de lista.
-
Especifica las dimensiones en forma de lista y crea una matriz (o un vector) con todos los elementos cero.
Sintaxis 1: Dim(Mat ) ; Dim(Vct )
Como el resultado del comando Dim es una lista, esta se guarda en List Ans.
Sintaxis 2: {,} → Dim(Mat ) (, = enteros, 1 ≤ ≤ 999, 1 ≤ ≤ 999) ;
{,} → Dim(Vct ) (, = enteros, 1 ≤ ≤ 999 cuando = 1, 1 ≤ ≤ 999 cuando = 1)
Complex Number
La letra de la siguiente sintaxis representa un número complejo. Los cálculos realizados con Arg, Ir∠θ y Ia+b se ven afectados por el ajuste S > [Angle].
Nota
La calculadora considera los números complejos en la forma a+b como coordenadas de un plano de Gauss, y calcula el valor absoluto || y el argumento Arg().
Norm of a Complex Number Abs()
Obtiene el valor absoluto de un número complejo.
Sintaxis: || Abs()
Ejemplo: |1+| =
Argument Arg()
Obtiene el argumento de un número complejo.
Sintaxis: Arg()
Ejemplo: Arg(1+) = (S > [Angle] > [Radian])
Complex Conjugate Conjg()
Obtiene el número complejo conjugado.
Sintaxis: Conjg()
Ejemplo: Conjg(1+) = 1
Real Part ReP()
Extrae la parte real de un número complejo.
Sintaxis: ReP()
Ejemplo: ReP(1+2) = 1
Imaginary Part ImP()
Extrae la parte imaginaria de un número complejo.
Sintaxis: ImP()
Ejemplo: ImP(1+2) = 2
Ir∠θ Ir∠θ
Convierte un valor en forma rectangular en un valor en forma polar.
Sintaxis: Ir∠θ
Ejemplo: Ir∠θ = 2∠ (S > [Angle] > [Radian])
Ia+b Ia+b
Convierte un valor en forma polar en un valor en forma rectangular.
Sintaxis: Ia+b
Ejemplo: 2∠Ia+b = (S > [Angle] > [Radian])
Statistics
En todas estas sintaxis, “List ” y “List ” son listas o variables de lista. Para las variables de lista, , puede ser un valor entre 1 y 26 o Ans. Las variables de lista también se pueden especificar mediante subnombres.
{} {}
Introduce llaves ( { } ) para introducir una nueva lista.
List List
Introduce “List ”. Después de “List ”, introduzca un valor entre 1 y 26 o Ans para especificar una variable de lista.
Dimensions Dim()
-
Determina el número de elementos de una lista.
-
Especifica el número de elementos de una lista y crea una variable de lista con cero en todos los elementos.
Sintaxis 1: Dim(List )
Sintaxis 2: Número de elementos → Dim(List ) ( = entero, 1 ≤ ≤ 999)
Fill List Fill(,)
Sustituye todos los valores de todos los elementos de una lista por el mismo valor ().
Sintaxis: Fill(,List )
Generate Sequence Seq(,,,,)
Define una función para generar una secuencia de números y devolverla en forma de lista.
Sintaxis: Seq(,,valor inicial,valor final,incremento)
puede ser cualquier variable alfabética.
Ejemplo: Seq(,,1,11,5) = {1,36,121}
Minimum Min()
Sintaxis 1: Min(List ) Extrae el valor mínimo de todos los elementos de una lista.
Sintaxis 2: Min(List ,List ) Extrae el elemento menor en la misma posición de dos listas.
Maximum Max()
Sintaxis 1: Max(List ) Extrae el valor máximo de todos los elementos de una lista.
Sintaxis 2: Max(List ,List ) Extrae el elemento mayor en la misma posición de dos listas.
Mean Mean()
Encuentra el valor de media de todos los elementos de una lista.
Sintaxis: Mean(List )
Median Median()
Encuentra la mediana de dos listas, una de ellas con datos y la otra con frecuencias.
Sintaxis: Median(List ,List )
List : lista de datos, List : lista de frecuencias
El número de elementos de List y List debe ser el mismo.
Ejemplo: Cuando List 1 = {36,16,58,46,56}, List 2 = {75,89,98,72,67}, Median(List 1,List 2) = 46
Combine Lists Augment(,)
Combina dos listas en una.
Sintaxis: Augment(List ,List )
Sum of List Elements Sum()
Encuentra la suma de todos los elementos de una lista.
Sintaxis: Sum(List )
List Product Prod()
Encuentra la suma producto de todos los elementos de una lista.
Sintaxis: Prod(List )
Cumulative Frequency Cuml()
Calcula la frecuencia acumulativa de los elementos de una lista.
Sintaxis: Cuml(List )
Ejemplo: Cuando List 1 = {2,3,6,5,4}, Cuml(List 1) = {2,5,11,16,20}
Data Percentages Percent()
Calcula el porcentaje de cada elemento relativo a la suma de todos los elementos de una lista.
Sintaxis: Percent(List )
List Data Diff ΔList
Calcula {Elemento 2 − Elemento 1, Elemento 3 − Elemento 2, ... Elemento − Elemento −1} en una lista de ( ≥ 2) elementos y devuelve el resultado en forma de lista.
Sintaxis: ΔList ( = número de variable de lista)
Nota: Para guardar el resultado en List 2, escriba “ΔList 1→List 2”.
Estimated x-Data
Estimated y-Data
Estas funciones se utilizan inmediatamente después de llevar a cabo un cálculo de regresión* con la aplicación Statistics. Para un valor especificado para una variable ( o ), estiman la otra variable en base a un modelo de regresión.
Sintaxis: Valor (calcula un valor estimado para el valor )
Valor (calcula un valor estimado para el valor )
No se pueden calcular valores estimados para los siguientes tipos de modelo de regresión: Med-Med Regression, Quadratic Regression, Cubic Regression, Quartic Regression, Sinusoidal Regression, Logarithm Regression.
Sample Standard Deviation StdDev()
Encuentra la desviación estándar de muestra de los datos especificados por una lista.
Sintaxis: StdDev(List [,List ]) (List ... datos de muestra, List ... datos de frecuencia)
Ejemplo: StdDev({10,20,30,40},{3,5,4,1}) = 9.26808696
Population Standard Deviation StdDev_σ()
Encuentra la desviación estándar de población de los datos especificados por una lista.
Sintaxis: StdDev_σ(List [,List ]) (List ... datos de muestra, List ... datos de frecuencia)
Unbiased Variance Variance()
Encuentra la desviación no sesgada de los datos especificados por una lista.
Sintaxis: Variance(List [,List ]) (List ... datos de muestra, List ... datos de frecuencia)
Population Variance Variance_()
Encuentra la desviación de población de los datos especificados por una lista.
Sintaxis: Variance_(List [,List ]) (List ... datos de muestra, List ... datos de frecuencia)
List to Matrix List→Mat()
Guarda el contenido de una lista en Mat Ans.
Sintaxis: List→Mat(List ,List )
(El número de elementos de List y List debe ser el mismo)
Ejemplo: Cuando List 1 = {2,3,4}, List 2 = {20,30,40}, List→Mat(List 1,List 2) =
Matrix to List Mat→List()
Guarda las columnas especificadas de una variable de matriz en List Ans.
Sintaxis: Mat→List(Mat ,)
( es una letra de la A a la Z o Ans, y es el número de columnas)
Ejemplo: Cuando Mat A = , Mat→List(Mat A,1) = {2,3,4}
Nota: Puede asignar los elementos de la columna 1 de Mat A a List 1 introduciendo “Mat→List(Mat A,1)→List 1”.
Distribution: Cálculo de probabilidad para una distribución normal estándar
Aviso para los usuarios de fx-1AU GRAPH
El modelo fx-1AU GRAPH no tiene una categoría Distribution, pero todos los comandos descritos en esta sección pueden llamarse desde C > [All].
Ejemplo: Para llamar “P()”, seleccione C > [All] > [P] > [P()].
Las funciones matemáticas descritas en esta sección están pensadas para usarse inmediatamente después de llevar a cabo el cálculo estadístico de una 1-Variable con la aplicación Statistics.
Normal Probability P(t) P()
Normal Probability Q(t) Q()
Normal Probability R(t) R()
Tomando la variable normalizada como argumento, estas funciones encuentran los valores de probabilidad para la distribución normal estándar mostrada en las siguientes figuras. El valor de se determina con la función t().
Sintaxis: P() ; Q() ; R()

Normal Variable t(x) t()
La variable normalizada t() en el valor de datos se determina con la siguiente fórmula en base a la media y la desviación estándar de población , que se obtiene como resultado del cálculo estadístico de 1-Variable.
Sintaxis: t()
Esta función se utiliza combinada con P(), Q() y R() para encontrar los valores de probabilidad de la distribución normal estándar.
Ejemplo: Se han introducido con la aplicación Statistics los datos de altura de 20 alumnos de una universidad y se ha llevado a cabo un cálculo estadístico de una 1-Variable. Determinar en qué percentil se encuentra el alumno de 180 cm de altura.
R(t(180))
Distribution: Cálculos de distribución
Aviso para los usuarios de fx-1AU GRAPH
El modelo fx-1AU GRAPH no tiene una categoría Distribution, pero todos los comandos descritos en esta sección pueden llamarse desde C > [All].
Ejemplo: Para llamar “NormPD()”, seleccione C > [All] > [N] > [NormPD()].
Las funciones de esta sección llevan a cabo tipos de cálculo de distribución diferentes.
Notas sobre la sintaxis
En la siguiente lista se muestra el significado de los símbolos y las abreviaturas de la sintaxis:
: valor de datos
Lower: límite inferior
Upper: límite superior
: media de población
: desviación estándar de población ( > 0)
: media ( > 0)
: probabilidad (0 ≤ ≤ 1)
df: grados de libertad (df > 0)
:df: grados de libertad del numerador (entero positivo)
:df: grados de libertad del denominador (entero positivo)
: probabilidad de éxito (0 ≤ ≤ 1)
: número de intentos desde la población (0 ≤ entero )
: número de éxitos en la población (0 ≤ entero )
: tamaño de la población ( ≤ , ≤ entero )
Los siguientes valores se sustituirán siempre que se omita alguno de los argumentos entre corchetes ([ ]).
=0, =1, tail=”L” (izquierda)
Variables de almacenamiento de resultados de cálculo
Se puede acceder a las variables (p, xInv, x1InvN, x2InvN, zLow, zUp, tLow, tUp) en las que se almacenan los resultados de cálculo de cada función desde C > [Variable Data] > [Distribution].
Normal Probability Density NormPD()
Devuelve la densidad de probabilidad normal (valor ) para los datos especificados.
Sintaxis: NormPD([,,])
Puede especificarse un valor o una lista para . El resultado de cálculo se asigna a las variables y Ans (List Ans cuando es una lista).
Ejemplo: NormPD(1) = 0.2419707245 ; NormPD({0.5,1}) = {0.3520653268,0.2419707245}
Normal Cumulative Dist NormCD(,)
Devuelve la distribución acumulada normal (valor ) para los datos especificados.
Sintaxis: NormCD(Lower,Upper[,,])
Pueden especificarse valores o listas para Lower y Upper. Los resultados de cálculo , zLow y zUp se asignan respectivamente a las variables , zLow y zUp. El resultado de cálculo también se asigna a Ans (List Ans cuando Lower y Upper son listas).
Ejemplo: NormCD(-1,1) = 0.6826894921 ; NormCD({-1,-2},{1,2}) = {0.6826894921,0.9544997361}
Inverse Normal Cumul Dist InvNormCD()
Devuelve la distribución acumulada normal inversa (valores Lower y/o Upper) para el valor especificado.
Sintaxis: InvNormCD([cola,][,,])
Puede especificar los valores “izquierda”, “derecha” o “centro” para “tail”. Para especificar el ajuste “tail”, introduzca los siguientes números o letras:
Izquierda: -1 o “L”
Centro: 0 o “C”
Derecha: 1 o “R”
Puede especificarse un valor o una lista para . Los resultados de cálculo se generarán de acuerdo con el ajuste de cola como se indica a continuación:
|
tail = Left |
El valor Upper se asigna a las variables x1InvN y Ans (List Ans cuando es una lista). |
|
tail = Right |
El valor Lower se asigna a las variables x1InvN y Ans (List Ans cuando es una lista). |
|
tail = Central |
Los valores Lower y Upper se asignan respectivamente a las variables x1InvN y x2InvN. Lower solo se asigna a Ans (List Ans cuando es una lista). |
Ejemplo:
InvNormCD(“L”,0.7,35,2) = 36.04880103
InvNormCD({0.5,0.7},35,2) = {35,36.04880103}
t Probability Density tPD(,)
Devuelve la densidad de probabilidad Student- (valor ) para los datos especificados.
Sintaxis: tPD(,df)
Consulte Sintaxis PD.
Ejemplo: tPD(1,1) = 0.1591549431 ; tPD({0,1},1) = {0.3183098862,0.1591549431}
t Cumulative Distribution tCD(,,)
Devuelve la distribución acumulada Student- (valor ) para los datos especificados.
Sintaxis: tCD(Lower,Upper,df)
Pueden especificarse valores o listas para Lower y Upper. Los resultados de cálculo , tLow y tUp se asignan respectivamente a las variables , tLow y tUp. El resultado de cálculo también se asigna a Ans (List Ans cuando Lower y Upper son listas).
Ejemplo: tCD(0,1,1) = 0.25 ; tCD({0,0},{1,2},1) = {0.25,0.3524163823}
Inverse t Cumulative Dist InvTCD(,)
Devuelve la distribución acumulada inversa Student- (valor Lower) para el valor especificado.
Sintaxis: InvTCD(,df)
Ejemplo: InvTCD(0.25,1) = 1 ; InvTCD({0.25,0.75},1) = {1,-1}
Probability Density ChiPD(,)
Devuelve la densidad de probabilidad (valor ) para los datos especificados.
Sintaxis: ChiPD(,df)
Consulte Sintaxis PD.
Ejemplo: ChiPD(1,1) = 0.2419707245 ; ChiPD({0,1},1) = {0,0.2419707245}
Cumulative Distribution ChiCD(,,)
Devuelve la distribución acumulada (valor ) para los datos especificados.
Sintaxis: ChiCD(Lower,Upper,df)
Consulte Sintaxis CD.
Ejemplo: ChiCD(0,1,1) = 0.6826894921 ; ChiCD({0,0},{1,2},1) = {0.6826894921,0.8427007929}
Inverse Cumulative Dist InvChiCD(,)
Devuelve la distribución acumulada inversa (valor Lower) para el valor especificado.
Sintaxis: InvChiCD(,df)
Ejemplo: InvChiCD(0.319,1) = 0.9930420738 ; InvChiCD({0.64,0.319},1) = {0.2187421667,0.9930420738}
F Probability Density FPD(,,)
Devuelve la densidad de probabilidad (valor ) para los datos especificados.
Sintaxis: FPD(,:df,:df)
Consulte Sintaxis PD.
Ejemplo: FPD(1,1,2) = 0.1924500897 ; FPD({1,2},1,2) = {0.1924500897,0.08838834765}
F Cumulative Distribution FCD(,,,)
Devuelve la distribución acumulada (valor ) para los datos especificados.
Sintaxis: FCD(Lower,Upper,:df,:df)
Consulte Sintaxis CD.
Ejemplo: FCD(0,1,1,2) = 0.5773502692 ; FCD({0,0},{1,2},1,2) = {0.5773502692,0.7071067812}
Inverse F Cumulative Dist InvFCD(,,)
Devuelve la distribución acumulada inversa (valor Lower) para el valor especificado.
Sintaxis: InvFCD(,:df,:df)
Ejemplo: InvFCD(0.43,1,2) = 0.9625240705 ; InvFCD({0.86,0.43},1,2) = {0.03998368013,0.9625240705}
Binomial Probability BinomialPD(,)
Devuelve la probabilidad binomial (valor ) para los datos especificados.
Sintaxis: BinomialPD([,],)
Consulte Sintaxis PD.
Ejemplo: BinomialPD(3,5,0.5) = 0.3125 ; BinomialPD({3,5},5,0.5) = {0.3125,0.03125}
Binomial Cumulative Dist BinomialCD(,)
Devuelve la distribución acumulada binomial (valor ) para los datos especificados.
Sintaxis: BinomialCD([[Lower,]Upper,],)
Consulte Sintaxis CD.
Ejemplo: BinomialCD(5,10,0.5) = 0.623046875 ; BinomialCD({0,5},{5,8},10,0.5) = {0.623046875,0.6123046875}
Inverse Binomial Cumulative Dist InvBinomialCD(,,)
Devuelve la distribución acumulada binomial inversa para el valor especificado.
Sintaxis: InvBinomialCD(,,)
Ejemplo: InvBinomialCD(0.6,10,0.5) = 5 ; InvBinomialCD({0.6,0.3},10,0.5) = {5,4}
Precauciones
Al ejecutar el cálculo de distribución acumulada binomial inversa, la calculadora utiliza el valor especificado y el valor que es uno menos que el número mínimo de dígitos significativos del valor (valor ’) para calcular los valores del número mínimo de intentos. Los resultados se asignan a variables xInv (resultado de cálculo usando ) y *xInv (resultado de cálculo usando ’). La calculadora solo muestra el valor xInv en todo momento. Sin embargo, cuando los valores xInv y *xInv sean diferentes, se mostrará el siguiente mensaje con ambos valores.
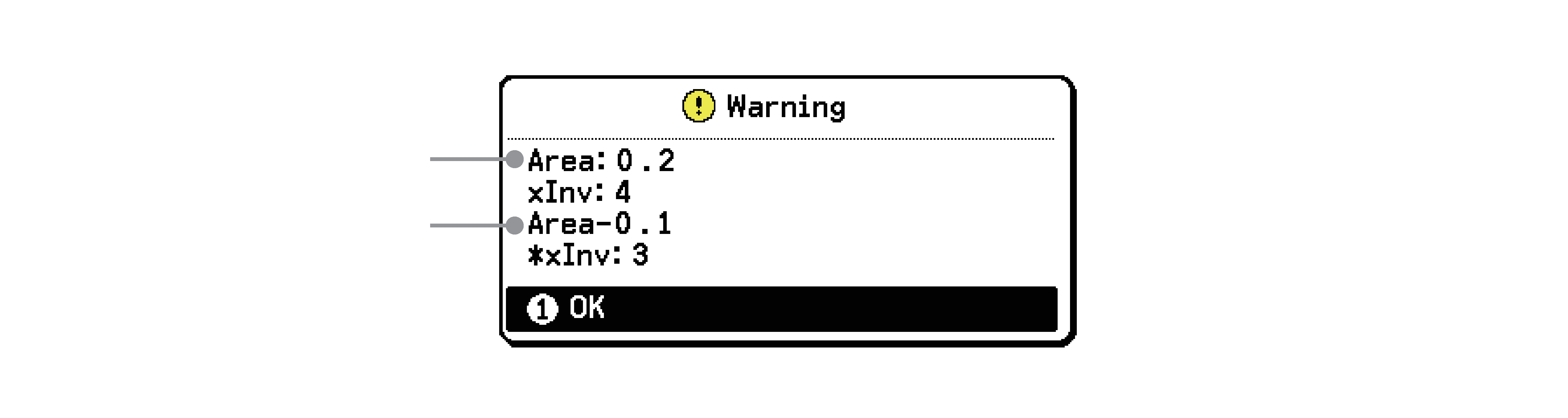
Valor
Valor ’
Los resultados de cálculo de la distribución acumulada binomial inversa son números enteros. La precisión puede verse reducida cuando el valor tiene 10 dígitos o más. Tenga en cuenta que incluso una ligera diferencia en la precisión de cálculo afecta a los resultados de cálculo. Si aparece un mensaje de advertencia, compruebe los valores mostrados.
Poisson Probability PoissonPD(,)
Devuelve la probabilidad de Poisson (valor ) para los datos especificados.
Sintaxis: PoissonPD(,)
Consulte Sintaxis PD.
Ejemplo: PoissonPD(1,1.2) = 0.3614330543 ; PoissonPD({1,2},1.2) = {0.3614330543,0.2168598326}
Poisson Cumulative Dist PoissonCD(,)
Devuelve la distribución acumulada de Poisson (valor ) para los datos especificados.
Sintaxis: PoissonCD([Lower,]Upper,)
Consulte Sintaxis CD.
Si se omite Lower, se asume que Lower = 0.
Ejemplo: PoissonCD(1,2,1.2) = 0.5782928869 ; PoissonCD({1,1},{2,3},1.2) = {0.5782928869,0.6650368199}
Inverse Poisson Cumul Dist InvPoissonCD(,)
Devuelve la distribución acumulada de Poisson inversa para el valor especificado.
Sintaxis: InvPoissonCD(,)
Ejemplo: InvPoissonCD(0.58,1.2) = 1 ; InvPoissonCD({0.58,0.75},1.2) = {1,2}
Las precauciones son las mismas que para Inverse Binomial Cumulative Dist.
Geometric Probability GeoPD(,)
Devuelve la probabilidad geométrica (valor ) para los datos especificados.
Sintaxis: GeoPD(,)
Consulte Sintaxis PD.
Ejemplo: GeoPD(2,0.8) = 0.16 ; GeoPD({2,3},0.8) = {0.16,0.032}
Geometric Cumulative Dist GeoCD(,)
Devuelve la distribución geométrica acumulada (valor ) para los datos especificados.
Sintaxis: GeoCD([Lower,]Upper,)
Consulte Sintaxis CD.
Si se omite Lower, se asume que Lower = 0.
Ejemplo: GeoCD(1,2,0.8) = 0.96 ; GeoCD({1,1},{2,3},0.8) = {0.96,0.992}
Inverse Geometric Cumul Dist InvGeoCD(,)
Devuelve la distribución geométrica acumulada inversa para el valor especificado.
Sintaxis: InvGeoCD(,)
Ejemplo: InvGeoCD(0.96,0.8) = 2 ; InvGeoCD({0.96,0.992},0.8) = {2,3}
Las precauciones son las mismas que para Inverse Binomial Cumulative Dist.
Hypergeometric Probability HypergeoPD(,,,)
Devuelve la probabilidad hipergeométrica (valor ) para los datos especificados.
Sintaxis: HypergeoPD(,,,)
Consulte Sintaxis PD.
Ejemplo: HypergeoPD(1,5,10,20) = 0.1354489164 ; HypergeoPD({1,2},5,10,20) = {0.1354489164,0.3482972136}
Hypergeometric Cumul Dist HypergeoCD(,,,)
Devuelve la distribución hipergeométrica acumulada (valor ) para los datos especificados.
Sintaxis: HypergeoCD([Lower,]Upper,,,)
Consulte Sintaxis CD.
Si se omite Lower, se asume que Lower = 0.
Ejemplo: HypergeoCD(1,2,5,10,20) = 0.48374613 ; HypergeoCD({1,1},{2,3},5,10,20) = {0.48374613,0.8320433437}
Inverse Hypergeo Cumul Dist InvHypergeoCD(,,,)
Devuelve la distribución hipergeométrica acumulada inversa para el valor especificado.
Sintaxis: InvHypergeoCD(,,,)
Ejemplo: InvHypergeoCD(0.48,5,10,20) = 2 ; InvHypergeoCD({0.48,0.83},5,10,20) = {2,3}
Las precauciones son las mismas que para Inverse Binomial Cumulative Dist.
Sintaxis y descripción
|
Sintaxis |
Descripción |
|---|---|
|
Sintaxis PD |
Puede especificarse un valor o una lista para . El resultado de cálculo se asigna a las variables y Ans (List Ans cuando es una lista). |
|
Sintaxis CD |
Pueden especificarse valores o listas para Lower y Upper. El resultado de cálculo se asigna a las variables y Ans (List Ans cuando Lower y Upper son listas). |
|
Sintaxis CD inversa (distribuciones continuas) |
Puede especificarse un valor o una lista para . El valor Lower se asigna a las variables xInv y Ans (List Ans cuando es una lista). |
|
Sintaxis CD inversa (distribuciones discretas) |
Puede especificarse un valor o una lista para . El resultado de cálculo del valor X se asigna a las variables xInv y Ans (List Ans cuando es una lista). |
Angle/Coord/Sexa
Degrees °
Especifica grados como unidad de ángulo.
Sintaxis: °
Ejemplo: Cuando S > [Angle] > [Radian], 90° =
Radians
Especifica radianes como unidad de ángulo.
Sintaxis:
Ejemplo: Cuando S > [Angle] > [Degree], = 90
Gradians
Especifica gradianes como unidad de ángulo.
Sintaxis:
Ejemplo: Cuando S > [Angle] > [Degree], = 90
Rectangular to Polar Pol(,)
Convierte los valores de coordenadas rectangulares a polares y los devuelve en forma de lista.
Sintaxis: Pol(,) = (,)
Las coordenadas polares resultantes se muestran en el siguiente rango en función del ajuste S > [Angle].
Degree: -180 < ≤ 180
Radian: - < ≤
Gradian: -200 < ≤ 200
Ejemplo: Cuando S > [Angle] > [Radian], Pol(,) = {2,}
Polar to Rectangular Rec(,)
Convierte los valores de coordenadas polares a rectangulares y los devuelve en forma de lista.
Sintaxis: Rec(,) = (,)
Ejemplo: Cuando S > [Angle] > [Radian], Rec(2,) = {,}
Degs Mins Secs °
Introduce un valor sexagesimal.
Sintaxis: Valor de grados°[Valor de minutos°[Valor de segundos°]]
Ejemplo: 1°15° = 1.25 ; 0°75° = 1.25 ; 0°15° = 0.25 ; 0°0°900° = 0.25
Nota: Para mostrar resultados de cálculo como valores sexagesimales, seleccione sF > [Sexagesimal]. Para obtener más información, consulte Cambiar el formato de visualización de los resultados de cálculo (menú Format).
Decimal to Sexagesimal IDMS
Convierte un valor decimal a sexagesimal (grados (horas), minutos, segundos).
Sintaxis: IDMS
Ejemplo: 1.25IDMS = 1°15’00”
Hyperbolic Calc
Las funciones hiperbólicas e hiperbólicas inversas pueden introducirse con los siguientes elementos del menú.
|
Elemento del menú |
Función |
|---|---|
|
sinh |
sinh() |
|
cosh |
cosh() |
|
tanh |
tanh() |
|
sinh |
sinh() |
|
cosh |
cosh() |
|
tanh |
tanh() |
Ejemplo: sinh(1) = 1.175201194 ; sinh(Ans) = 1
Engineer Symbol
Pueden introducirse símbolos de ingeniería con los siguientes elementos de menú.
|
Elemento del menú |
Símbolo |
|
|---|---|---|
|
Milli |
m |
|
|
Micro |
μ |
|
|
Nano |
n |
|
|
Pico |
p |
|
|
Femto |
f |
|
|
Kilo |
k |
|
|
Mega |
M |
|
|
Giga |
G |
|
|
Tera |
T |
|
|
Peta |
P |
|
|
Exa |
E |
Al añadir un símbolo de ingeniería justo después de un valor, este se convierte en (donde es un entero múltiplo de 3).
Ejemplo: 7.1k = 7100 ; 2G÷100M = 20
Nota: Para visualizar resultados de cálculo con símbolos de ingeniería, active S > [Display] > [Engineer Symbol]. Para obtener más detalles, consulte Display (general).
Unit Conversions
Convierte un valor de una unidad a otra unidad diferente.
Sintaxis: Comando de unidad ![]() comando de unidad (= número real o lista de números reales)
comando de unidad (= número real o lista de números reales)
Los dos comandos de unidad se enlazan con “![]() ” y se utilizan como un único comando de conversión de unidades. Los dos comandos de unidad deben ser de la misma categoría. Consulte la siguiente “Lista de comandos de unidad” para ver todos los comandos disponibles.
” y se utilizan como un único comando de conversión de unidades. Los dos comandos de unidad deben ser de la misma categoría. Consulte la siguiente “Lista de comandos de unidad” para ver todos los comandos disponibles.
Ejemplo:
25.4 [cm] ![]() [in] = 10 ; {175,162} [m2]
[in] = 10 ; {175,162} [m2] ![]() [ha] = {0.0175,0.0162}
[ha] = {0.0175,0.0162}
Lista de comandos de unidad
|
Categoría |
Comando de unidad |
|---|---|
|
Length |
[fm] |
|
[Å] |
|
|
[μm] |
|
|
[mm] |
|
|
[cm] |
|
|
[m] |
|
|
[km] |
|
|
[AU] |
|
|
[l.y.] |
|
|
[pc] |
|
|
[Mil] |
|
|
[in] |
|
|
[ft] |
|
|
[yd] |
|
|
[fath] |
|
|
[rd] |
|
|
[mile] |
|
|
[n mile] |
|
|
Area |
[cm2] |
|
[m2] |
|
|
[ha] |
|
|
[km2] |
|
|
[in2] |
|
|
[ft2] |
|
|
[yd2] |
|
|
[acre] |
|
|
[mile2] |
|
|
Volume |
[cm3] |
|
[mL] |
|
|
[L] |
|
|
[m3] |
|
|
[in3] |
|
|
[ft3] |
|
|
[fl_oz(UK)] |
|
|
[fl_oz(US)] |
|
|
[gal(US)] |
|
|
[gal(UK)] |
|
|
[pt] |
|
|
[qt] |
|
|
[tsp] |
|
|
[tbsp] |
|
|
[cup] |
|
|
Time |
[ns] |
|
[μs] |
|
|
[ms] |
|
|
[s] |
|
|
[min] |
|
|
[h] |
|
|
[day] |
|
|
[week] |
|
|
[yr] |
|
|
[s-yr] |
|
|
[t-yr] |
|
|
Temperature |
[°C] |
|
[K] |
|
|
[°F] |
|
|
[°R] |
|
|
Velocity |
[m/s] |
|
[km/h] |
|
|
[knot] |
|
|
[ft/s] |
|
|
[mile/h] |
|
|
Mass |
[u] |
|
[mg] |
|
|
[g] |
|
|
[kg] |
|
|
[mton] |
|
|
[oz] |
|
|
[lb] |
|
|
[slug] |
|
|
[ton(short)] |
|
|
[ton(long)] |
|
|
Force |
[N] |
|
[lbf] |
|
|
[tonf] |
|
|
[dyne] |
|
|
[kgf] |
|
|
Pressure |
[Pa] |
|
[kPa] |
|
|
[mmH2O] |
|
|
[mmHg] |
|
|
[atm] |
|
|
[inH2O] |
|
|
[inHg] |
|
|
[lbf/in2] |
|
|
[bar] |
|
|
[kgf/cm2] |
|
|
Energy |
[eV] |
|
[J] |
|
|
[calth] |
|
|
[cal15] |
|
|
[calIT] |
|
|
[kcalth] |
|
|
[kcal15] |
|
|
[kcalIT] |
|
|
[l-atm] |
|
|
[kW・h] |
|
|
[ft・lbf] |
|
|
[Btu] |
|
|
[erg] |
|
|
[kgf・m] |
|
|
Power |
[W] |
|
[calth/s] |
|
|
[hp] |
|
|
[ft・lbf/s] |
|
|
[Btu/min] |
Variable Data
La categoría Variable Data contiene variables que almacenan valores de entrada y salida de cada aplicación. Los elementos del menú que se muestran al seleccionar C > [Variable Data] son nombres de aplicaciones.

Variable Data > Statistics
Las variables de esta categoría almacenan valores de introducción, resultados de cálculos estadísticos realizados y gráficos dibujados con la aplicación Statistics.
Statistics > X
Valores de datos de cálculo estadístico de variables simples o emparejadas:
|
Elemento del menú |
Variable |
|---|---|
|
Data Items |
n |
|
Data x Mean |
|
|
Data x Sum |
|
|
x-Data Sum of Squares |
|
|
x-Data Population Std Dev |
σx |
|
x-Data Sample Std Dev |
sx |
|
X-Data Minimum |
minX |
|
X-Data Maximum |
maxX |
Statistics > Y
Valores de datos de cálculo estadístico de variables emparejadas:
|
Elemento del menú |
Variable |
|---|---|
|
Data y Mean |
|
|
Data y Sum |
|
|
y-Data Sum of Squares |
|
|
xy-Data Products Sum |
|
|
y-Data Population Std Dev |
σy |
|
y-Data Sample Std Dev |
sy |
|
Y-Data Minimum |
minY |
|
Y-Data Maximum |
maxY |
Statistics > Graph
Valores de información sobre el modelo de regresión:
|
Elemento del menú |
Variable |
|---|---|
|
a Regression Coefficient |
a |
|
b Regression Coefficient |
b |
|
c Regression Coefficient |
c |
|
d Regression Coefficient |
d |
|
e Regression Coefficient |
e |
|
Correlation Coefficient |
r |
|
Coefficient of Determination |
|
|
Error Mean Square |
MSe |
Valores de salida de cálculo estadístico de variables simples:
|
Elemento del menú |
Variable |
|---|---|
|
1st Quartile |
|
|
Input Data Median |
Med |
|
3rd Quartile |
|
|
Input Data Mode |
Mod |
Statistics > Point Coordinates
Coordenadas de puntos resumen cuando se lleva a cabo Med-Med Regression:
|
Elemento del menú |
Variable |
|---|---|
|
Summary Point Coords |
|
|
Summary Point Coords |
|
|
Summary Point Coords |
|
|
Summary Point Coords |
|
|
Summary Point Coords |
|
|
Summary Point Coords |
Statistics > Input
Valores de introducción de cálculos estadísticos:
|
Elemento del menú |
Variable |
|---|---|
|
Sample Size |
n |
|
Sample Mean |
|
|
Sample Standard Deviation |
sx |
|
Sample 1 Size |
n1 |
|
Sample 2 Size |
n2 |
|
Sample 1 Mean |
1 |
|
Sample 2 Mean |
2 |
|
Sample 1 Standard Deviation |
sx1 |
|
Sample 2 Standard Deviation |
sx2 |
|
Sample p Standard Deviation |
sp |
Statistics > Result > Test
Resultados de cálculo de las pruebas:
|
Elemento del menú |
Variable |
|---|---|
|
p |
p |
|
z |
z |
|
t |
t |
|
F |
F |
|
Estimated Sample Proportion |
|
|
Estim Sample 1 Proportion |
1 |
|
Estim Sample 2 Proportion |
2 |
|
Degree of Freedom |
df |
|
Standard Error |
se |
|
Correlation Coefficient |
r |
|
Coefficient of Determination |
|
|
p Value of Factor A |
pa |
|
F Value of Factor A |
Fa |
|
Factor A Degrees of Freedom |
Adf |
|
Factor A Sum of Squares |
SSa |
|
Factor A Mean Squares |
MSa |
|
p Value of Factor B |
pb |
|
F Value of Factor B |
Fb |
|
Factor B Degrees of Freedom |
Bdf |
|
Factor B Sum of Squares |
SSb |
|
Factor B Mean Squares |
MSb |
|
Factor AB p Value |
pab |
|
Factor AB F Value |
Fab |
|
Factor AB Deg of Freedom |
ABdf |
|
Factor AB Sum of Squares |
SSab |
|
Factor AB Mean Squares |
MSab |
|
Error Degrees of Freedom |
Edf |
|
Error Sum of Squares |
SSe |
|
Error Mean Square |
MSe |
Statistics > Result > Confidence Interval
Resultados de cálculo del intervalo de confianza:
|
Elemento del menú |
Variable |
|---|---|
|
Confidence Int Lower Limit |
Lower |
|
Confidence Int Upper Limit |
Upper |
|
Estimated Sample Proportion |
|
|
Estim Sample 1 Proportion |
1 |
|
Estim Sample 2 Proportion |
2 |
|
Degree of Freedom |
df |
Variable Data > Distribution
Las variables de esta categoría almacenan los resultados de los cálculos de distribución realizados con la aplicación Distribution.
|
Elemento del menú |
Variable |
|---|---|
|
p |
p |
|
x Inverse |
xInv |
|
x1 Inverse |
x1InvN |
|
x2 Inverse |
x2InvN |
|
Normal Cumulative Dist Lower |
zLow |
|
Normal Cumulative Dist Upper |
zUp |
|
t Cumulative Dist Lower |
tLow |
|
t Cumulative Dist Upper |
tUp |
Variable Data > Table
|
Elemento del menú |
Variable |
Descripción |
|---|---|---|
|
Function Table Result |
F Result |
Genera el contenido de la pestaña Table de la aplicación Graph&Table en forma de matriz. |
Variable Data > Recursion
|
Elemento del menú |
Variable |
Descripción |
|---|---|---|
|
Recursion Table Result |
R Result |
Genera el contenido de la pestaña Table de la aplicación Recursion en forma de matriz. |
Variable Data > Equation
Las variables de esta categoría almacenan valores de introducción y resultados de cálculo para ecuaciones de orden superior o ecuaciones simultáneas resueltos con la aplicación Equation.
|
Elemento del menú |
Variable |
Descripción |
|---|---|---|
|
Hi-Ord Coeff |
Ply Coef |
Genera coeficientes de entrada de ecuaciones de orden superior en forma de matriz. |
|
Hi-Ord Solutions |
Ply Result |
Genera resultados de cálculo de ecuaciones de orden superior en forma de matriz. |
|
Linear Coeffs |
Sim Coef |
Genera coeficientes de entrada de ecuaciones simultáneas en forma de matriz. |
|
Linear Solutions |
Sim Result |
Genera resultados de cálculo de ecuaciones simultáneas en forma de matriz. |
All > A a Z
C > [All] ofrece una lista ordenada alfabéticamente de todas las funciones, los comandos y las variables de las aplicaciones. Para obtener más detalles, consulte Detalles del menú Catalog.
All > Symbol
Este menú incluye las funciones y símbolos de la siguiente tabla:
|
() |
! |
∠ |
E (Engineer Symbol) |
|
^() |
° (Degrees) |
: |
P (Engineer Symbol) |
|
{ |
(Radians) |
|
T (Engineer Symbol) |
|
} |
(Gradians) |
= |
G (Engineer Symbol) |
|
≠ |
° |
$ |
M (Engineer Symbol) |
|
< |
() |
, |
k (Engineer Symbol) |
|
> |
( |
m (Engineer Symbol) |
|
|
≤ |
) |
(Engineer Symbol) |
|
|
≥ |
[ |
n (Engineer Symbol) |
|
|
” |
^ |
] |
p (Engineer Symbol) |
|
~ |
|
|
f (Engineer Symbol) |
|
- |
|
|