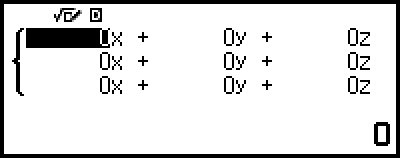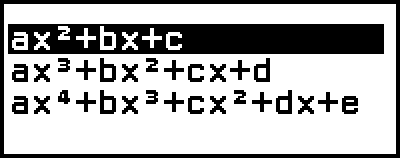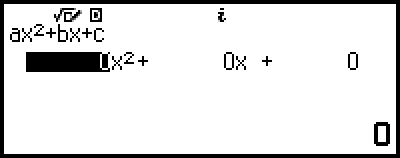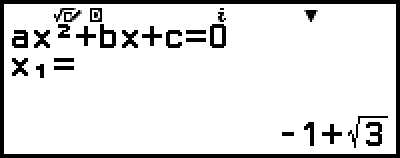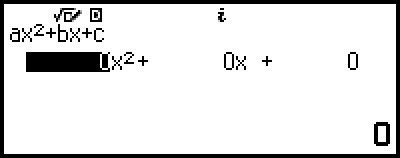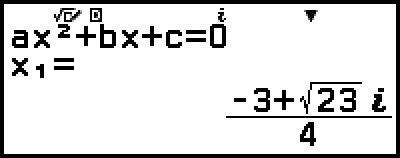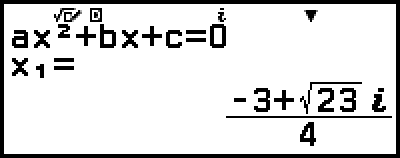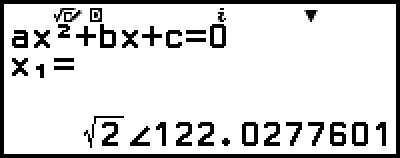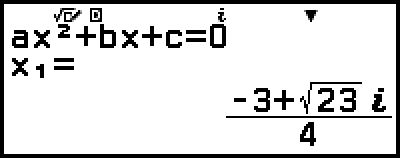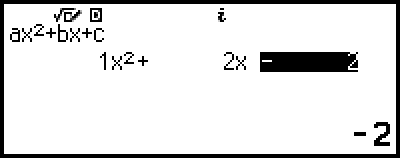Cálculos de ecuaciones
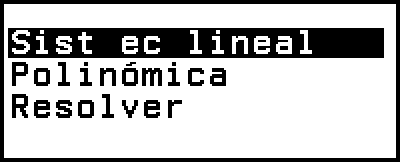
La aplicación Ecuación incluye las tres funciones descritas a continuación. Después de iniciar la aplicación, puede usar el menú Ecuación que aparece para seleccionar la función que desee.

Sist ec lineal: Ecuaciones lineales simultáneas con dos, tres o cuatro incógnitas
Polinómica: Ecuaciones de grado superior cuadráticas, cúbicas o cuárticas
Resolver: Función que busca el valor de cualquier variable contenida en una ecuación
Ecuaciones lineales simultáneas
En este apartado se explica el procedimiento general para resolver una ecuación simultánea con un ejemplo que resuelve una ecuación lineal simultánea con tres incógnitas.
Ejemplo 1: 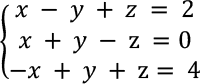
1. Pulse  , seleccione el icono de la aplicación Ecuación y, después, pulse
, seleccione el icono de la aplicación Ecuación y, después, pulse  .
.
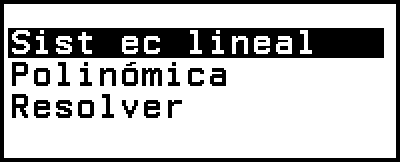
Se muestra el menú Ecuación.
2. Seleccione [Sist ec lineal] y, luego, pulse  .
.
Se mostrará el menú del número de incógnitas.
3. Seleccione [3 incógnitas] y, luego, pulse  .
.
Se muestra el editor de coeficientes.
4. Use el editor de coeficientes para introducir los valores de los coeficientes.
- 1


 ((-))1
((-))1 1
1 2
2
1 1
1

 ((-))1
((-))1 0
0

 ((-))1
((-))1 1
1 1
1 4
4
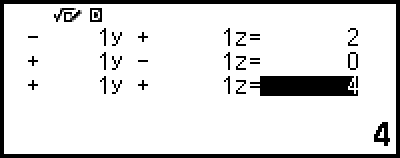
Si se pulsa  mientras se muestra el editor de coeficientes, todos los coeficientes se ponen a cero.
mientras se muestra el editor de coeficientes, todos los coeficientes se ponen a cero.
5. Pulse  .
.
Se mostrará una solución.
Cuando el indicador  aparezca en la pantalla, cada vez que se pulse
aparezca en la pantalla, cada vez que se pulse  (o
(o  ) se verá otra solución.
) se verá otra solución.
 (o
(o  )
) 
 (o
(o  )
) 
Si se pulsa  o
o  cuando el indicador
cuando el indicador  esté en la pantalla, se verá de nuevo la solución mostrada justo antes.
esté en la pantalla, se verá de nuevo la solución mostrada justo antes.
Si se pulsa  cuando se visualice la última solución, se vuelve al editor de coeficientes. Para volver al editor de coeficientes cuando se esté visualizando cualquier solución, pulse
cuando se visualice la última solución, se vuelve al editor de coeficientes. Para volver al editor de coeficientes cuando se esté visualizando cualquier solución, pulse  .
.
Al pulsar  mientras se muestre el editor de coeficientes, se vuelve al menú del número de incógnitas.
mientras se muestre el editor de coeficientes, se vuelve al menú del número de incógnitas.
Nota
Mientras se muestra el editor de coeficientes, puede guardar el valor resaltado actualmente en una variable. De igual modo, mientras se muestran las soluciones, aquella mostrada en cada momento puede guardarse en una variable. Para obtener más información sobre las variables, consulte “Variables (A, B, C, D, E, F, x, y, z)”.
Ecuaciones de grado superior cuadráticas, cúbicas o cuárticas
Al resolver una ecuación de grado superior con la aplicación Ecuación, se muestran los valores siguientes según el grado de la ecuación.
Ecuación cuadrática
Después de visualizarse la solución de ax2+bx+c=0, se muestran las coordenadas mínimas (o máximas) (x, y) de y=ax2+bx+c.
Ecuación cúbica
Después de visualizarse la solución de ax3+bx2+cx+d=0, se muestran las coordenadas (x, y) del mínimo local (o máximo local) de y=ax3+bx2+cx+d, solo en caso de que dicho mínimo o máximo local exista. Si no existe el mínimo o máximo local y se pulsa  mientras se muestra la última solución, aparece el mensaje “Sin máx/mín local”.
mientras se muestra la última solución, aparece el mensaje “Sin máx/mín local”.
Ecuación cuártica
Se muestra la solución de ax4+bx3+cx2+dx+e=0.
A continuación, veremos un ejemplo de una ecuación cuadrática para explicar el procedimiento general de resolución de ecuaciones de grado superior.
Ejemplo 2: x2 + 2x − 2 = 0
(Entrada/Salida: E Mat/S Mat)
1. Pulse  , seleccione el icono de la aplicación Ecuación y, después, pulse
, seleccione el icono de la aplicación Ecuación y, después, pulse  .
.
Se muestra el menú Ecuación.
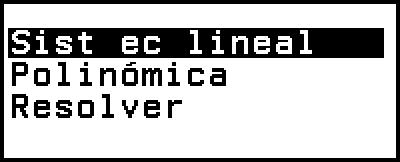
2. Seleccione [Polinómica] y, luego, pulse  .
.
Se mostrará el menú del número de grados.
3. Seleccione [ax2+bx+c] y, luego, pulse  .
.
Se muestra el editor de coeficientes.
4. Use el editor de coeficientes para introducir los valores de los coeficientes.
- 1
 2
2

 ((-))2
((-))2
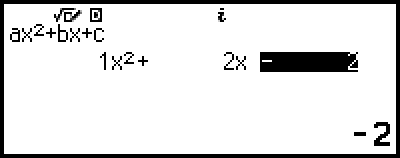
Si se pulsa  mientras se muestra el editor de coeficientes, todos los coeficientes se ponen a cero.
mientras se muestra el editor de coeficientes, todos los coeficientes se ponen a cero.
5. Pulse  .
.
Se mostrará una solución.
Cuando el indicador  aparezca en la pantalla, cada vez que se pulse
aparezca en la pantalla, cada vez que se pulse  (o
(o  ) se verá el resultado de otro cálculo (solución o coordenada).
) se verá el resultado de otro cálculo (solución o coordenada).
 (o
(o  )
) 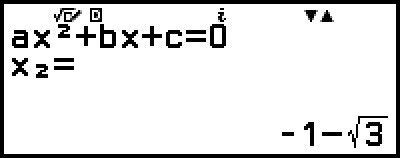
(Muestra la coordenada x del mínimo de y = x2 + 2x − 2.)
 (o
(o  )
) 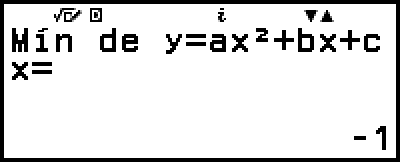
(Muestra la coordenada y del mínimo de y = x2 + 2x − 2.)
 (o
(o  )
)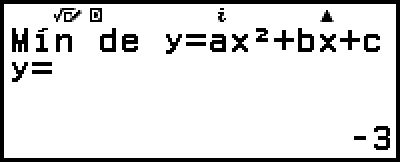
Si se pulsa  o
o  cuando el indicador
cuando el indicador  esté en la pantalla, se verá de nuevo el resultado del cálculo mostrado justo antes.
esté en la pantalla, se verá de nuevo el resultado del cálculo mostrado justo antes.
Si se pulsa  cuando se esté visualizando el último resultado de un cálculo, se vuelve al editor de coeficientes. Para volver al editor de coeficientes cuando se esté visualizando cualquier resultado de un cálculo, pulse
cuando se esté visualizando el último resultado de un cálculo, se vuelve al editor de coeficientes. Para volver al editor de coeficientes cuando se esté visualizando cualquier resultado de un cálculo, pulse  .
.
Al pulsar  mientras se muestre el editor de coeficientes, se vuelve al menú del número de grados.
mientras se muestre el editor de coeficientes, se vuelve al menú del número de grados.
Nota
Mientras se muestra el editor de coeficientes, puede guardar el valor resaltado actualmente en una variable. Asimismo, mientras se muestra el resultado de un cálculo (solución o coordenada), este se puede guardar en una variable. Para obtener más información sobre las variables, consulte “Variables (A, B, C, D, E, F, x, y, z)”.
Visualización de la solución de números complejos (Raíz compleja)
Las ecuaciones de grado superior pueden tener soluciones de números complejos. Cuando se selecciona Polinómica en el menú Ecuación, se pueden llevar a cabo las siguientes operaciones para activar o desactivar la visualización de la solución de números complejos.
 – [Raíz compleja] > [On]
– [Raíz compleja] > [On] 
Activa la visualización de la solución de números complejos (ajuste inicial por defecto).
 – [Raíz compleja] > [Off]
– [Raíz compleja] > [Off] 
Desactiva la visualización de la solución de números complejos. Si se introduce y se ejecuta una ecuación que solo tiene una o varias soluciones de números complejos, aparece el mensaje “Raíces no reales”.
Ejemplo 3: 2x2 + 3x + 4 = 0
(Entrada/Salida: E Mat/S Mat, Result complejo: a+bi, Raíz compleja: On)
1. Pulse  , seleccione el icono de la aplicación Ecuación y, después, pulse
, seleccione el icono de la aplicación Ecuación y, después, pulse  .
.
Se muestra el menú Ecuación.
2. Seleccione [Polinómica] > [ax2+bx+c].
Se muestra el editor de coeficientes.
3. Use el editor de coeficientes para introducir los valores de los coeficientes.
- 2
 3
3 4
4

4. Pulse  .
.
Se mostrará una solución.
5. Visualice otra solución y otros valores de coordenadas.
 (o
(o  )
) 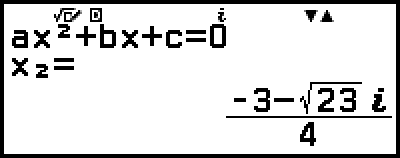
 (o
(o  )
) 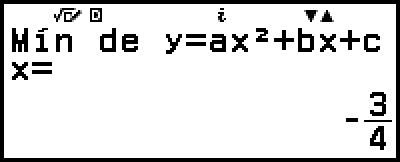
 (o
(o  )
)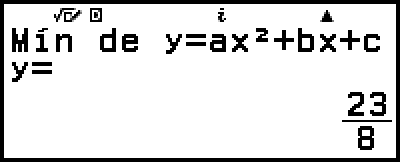
Si se pulsa  cuando se esté visualizando el último resultado de un cálculo, se vuelve al editor de coeficientes. Para volver al editor de coeficientes cuando se esté visualizando cualquier resultado de un cálculo, pulse
cuando se esté visualizando el último resultado de un cálculo, se vuelve al editor de coeficientes. Para volver al editor de coeficientes cuando se esté visualizando cualquier resultado de un cálculo, pulse  .
.
Conversión de una solución de números complejos en coordenadas rectangulares o polares
Para convertir una solución de números complejos al formato de coordenadas rectangulares o polares, puede usar el menú FORMAT que aparece al pulsar  .
.
Ejemplo 4: Convertir la solución de números complejos mostrada en el ejemplo 3 a formato de coordenadas polares y, luego, a formato de coordenadas rectangulares
1. Siga los pasos del 1 al 4 del ejemplo 3.
2. Pulse  , seleccione [Coord polares] y, después, pulse
, seleccione [Coord polares] y, después, pulse  .
.
Así se convierte la solución al formato de coordenadas polares.
3. Pulse  , seleccione [Coord rectang] y, después, pulse
, seleccione [Coord rectang] y, después, pulse  .
.
Así se convierte la solución al formato de coordenadas rectangulares.
Uso de Resolver
Resolver utiliza el método de Newton para aproximar la solución de las ecuaciones. Esta función admite la introducción de ecuaciones en los siguientes formatos.
Ejemplos: y = x + 5, x = sen(A), xy + C (xy + C tiene el valor 0)
Ejemplo 5: Resolver x2 - B2 = 0 para x cuando B = 4
(Entrada/Salida: E Mat/S Mat)
Nota
Antes de resolver x2 - B2 = 0 para x, 4 se debe guardar en la variable B. Esto se realiza en el paso 3 del procedimiento detallado a continuación.
1. Pulse  , seleccione el icono de la aplicación Ecuación y, después, pulse
, seleccione el icono de la aplicación Ecuación y, después, pulse  .
.
Se muestra el menú Ecuación.
2. Seleccione [Resolver] y, luego, pulse  .
.
Se muestra la pantalla de introducción de ecuaciones Resolver.
3. Guarde 4 en la variable B.
 4
4

Esta operación puede ejecutarse en cualquier momento anterior al paso 7 de este procedimiento.
Para obtener más información sobre las variables, consulte “Variables (A, B, C, D, E, F, x, y, z)”.
Pulse  para volver a la pantalla de introducción de ecuaciones Resolver.
para volver a la pantalla de introducción de ecuaciones Resolver.
4. Introduzca la ecuación.



 (B)
(B) 2
2

 (=)*0
(=)*0
* También puede realizar la operación siguiente para introducir el signo =:  – [Ecuación] > [=].
– [Ecuación] > [=].
5. Pulse  para registrar la ecuación.
para registrar la ecuación.
6. En la pantalla Escoger incógnita, confirme que está seleccionada la [x] y pulse  .
.
Se muestra una pantalla con el valor inicial de x.
7. Introduzca 1 como valor inicial de x.
- 1


8. Tras comprobar si [Ejecutar] está seleccionado, pulse  para resolver la ecuación.
para resolver la ecuación.
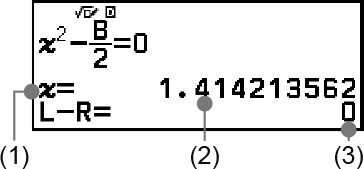
(1) Variable resuelta para
(2) Solución
(3) Resultado (lado izquierdo) − (lado derecho)
Las soluciones siempre se muestran en forma decimal.
Cuanto más se acerque el resultado (lado izquierdo) − (lado derecho) a cero, mayor será la precisión de la solución.
9. A continuación, pulse la tecla de la operación que desee realizar.
| Para hacer esto: | Pulse esta tecla: |
|---|---|
| Volver a la pantalla del paso 6. |  * * |
| Guardar la expresión introducida y volver a la pantalla del paso 4. |  o o  |
* El valor inicial al pulsar esta tecla se convierte en el último valor inicial utilizado para el cálculo.
¡Importante!
-
Resolver realiza la convergencia un número preestablecido de veces. Si no se encuentra ninguna solución, aparece una pantalla de confirmación, parecida a la situada a la derecha, en la que se pregunta si desea continuar. Pulse
 cuando esté seleccionada la opción [Continuar] para continuar o seleccione [Salir] y, luego,
cuando esté seleccionada la opción [Continuar] para continuar o seleccione [Salir] y, luego,  para cancelar la operación Resolver.
para cancelar la operación Resolver. 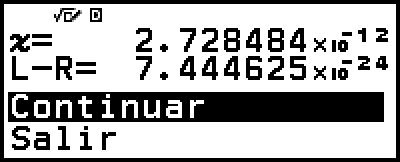
Según lo que haya introducido como valor inicial en la variable de solución (x en el ejemplo anterior), es posible que Resolver no halle una solución. Si es el caso, cambie el valor inicial para que sea más próximo a la solución.
Es posible que Resolver no pueda determinar la solución correcta aunque dicha solución exista.
Resolver utiliza el método de Newton, de modo que, aunque haya varias soluciones, solo se indicará una.
Dadas las limitaciones del método de Newton, suele ser difícil obtener soluciones en ecuaciones como las siguientes: y=senx, y=ex, y=√x.
Uso de Verificar con la aplicación Ecuación
La aplicación Ecuación permite usar Verificar con ecuaciones simultáneas o de grado superior. Al activar Verificar con la aplicación Ecuación, en lugar de la solución aparece un menú de respuesta como el que se muestra debajo.

Después de usar este menú para introducir una respuesta (bien seleccionando [Introducir sol] y, luego, introduciendo una solución, o bien seleccionando [Sin solución] o [Infin soluciones]), la calculadora indica si su respuesta es verdadera.
Nota
El menú anterior aparece en el caso de Sist ec lineal. En el caso de Polinómica aparece otro menú.
Verificar puede usarse con varias aplicaciones de la calculadora. Antes de efectuar las operaciones de esta sección, lea la información contenida en “Descripción de Verificar”.
Verificar no se puede usar con las funciones de la aplicación Ecuación que se indican a continuación.
- [Sist ec lineal] > [3 incógnitas] o [4 incógnitas]
- [Polinómica] > [ax3+bx2+cx+d] o [ax4+bx3+cx2+dx+e]
- [Resolver]
Al seleccionar cualquiera de las opciones de menú anteriores en el menú Ecuación cuando Verificar está activado, aparece el mensaje “No compatible con Verificar” en la pantalla.
Ejemplo de operación Verificar
Ejemplo 6: Introducir las dos soluciones (x1 = -1 + √3, x2 = -1 - √3) de la ecuación x2 + 2x - 2 = 0 resuelta en el ejemplo 2 y determinar si son verdaderas. Además, seleccionar si esta ecuación tiene un valor mínimo o un valor máximo, introducir los valores de las coordenadas (x, y) y determinar si los valores son verdaderos.
1. Siga los pasos del 1 al 4 del ejemplo 2.
2. Para activar Verificar, pulse  y, luego, seleccione [Verificar ON].
y, luego, seleccione [Verificar ON].
Aparece el indicador  en la parte superior de la pantalla, lo cual indica que Verificar se ha activado.
en la parte superior de la pantalla, lo cual indica que Verificar se ha activado.
3. Pulse  .
.
Se muestra el menú de respuesta de la ecuación cuadrática.
4. Confirme si [Solución] está seleccionado y, luego, pulse  .
.
Se mostrará el menú del número de soluciones.
5. Seleccione [2 soluciones] y, después, pulse  .
.
6. En la pantalla de introducción de soluciones que aparece, introduzca x1 y x2.

 ((-))1
((-))1
 3
3


 ((-))1
((-))1
 3
3

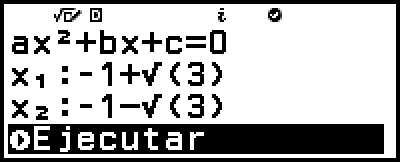
7. Confirme si [Ejecutar] está seleccionado y, luego, pulse  .
.
En la pantalla aparece “Verdadero” si el número de soluciones y todas las soluciones introducidas son correctos.
En la pantalla aparece “Falso” si el número de soluciones o la solución introducida son incorrectos. Pulse  o
o  para volver a la pantalla de introducción de soluciones e introduzca nuevamente el valor. Para cambiar la selección del número de soluciones, pulse
para volver a la pantalla de introducción de soluciones e introduzca nuevamente el valor. Para cambiar la selección del número de soluciones, pulse  en la pantalla de introducción de soluciones y comience de nuevo desde el paso 4.
en la pantalla de introducción de soluciones y comience de nuevo desde el paso 4.
8. Confirme si [Volver al inicio] está seleccionado y, luego, pulse  .
.
Al hacerlo, volverá al editor de coeficientes indicado en el paso 1 de este procedimiento.
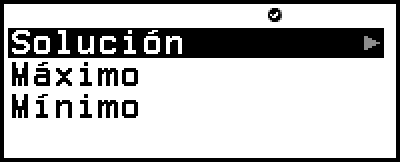
9. Pulse  para mostrar el menú de respuesta y, luego, seleccione [Máximo] o [Mínimo].
para mostrar el menú de respuesta y, luego, seleccione [Máximo] o [Mínimo].
La ecuación x2 + 2x - 2 = 0 tiene un valor mínimo, de modo que seleccione [Mínimo] y, luego, pulse  .
.
10. En la pantalla de introducción de los valores de coordenadas que aparece, introduzca x e y.

 ((-))1
((-))1

 ((-))3
((-))3
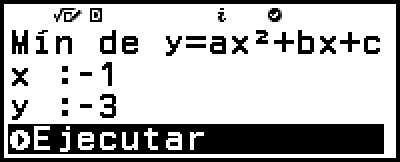
11. Confirme si [Ejecutar] está seleccionado y, luego, pulse  .
.
En la pantalla aparece “Verdadero” cuando la selección del valor máximo o mínimo y todos los valores de coordenadas introducidos son correctos.
En la pantalla aparece “Falso” cuando la selección del valor máximo o mínimo o un valor de coordenada introducido son incorrectos. Si esto ocurre, pulse  o
o  para volver a la pantalla de introducción de valores de coordenadas e introduzca nuevamente los valores. Si desea cambiar la selección del valor máximo/mínimo, pulse
para volver a la pantalla de introducción de valores de coordenadas e introduzca nuevamente los valores. Si desea cambiar la selección del valor máximo/mínimo, pulse  en la pantalla de introducción de valores de coordenadas y repita los pasos desde el 9.
en la pantalla de introducción de valores de coordenadas y repita los pasos desde el 9.
12. Confirme si [Volver al inicio] está seleccionado y, luego, pulse  .
.
Al hacerlo, volverá al editor de coeficientes indicado en el paso 1 de este procedimiento.
13. Para desactivar Verificar y salir de la operación de Verificar, pulse  y, a continuación, seleccione [Verificar OFF].
y, a continuación, seleccione [Verificar OFF].
Al hacerlo, el indicador  desaparece de la pantalla.
desaparece de la pantalla.
Para obtener información sobre cómo desactivar Verificar, consulte “Para desactivar Verificar”.
Nota
Puede ver la solución y el valor mínimo seleccionando [Confirm solución] en el paso 8 o el 12 de este procedimiento y, luego, pulsando  . La pantalla que aparece y las operaciones que se pueden efectuar son las mismas que las indicadas en el paso 5 del ejemplo 2.
. La pantalla que aparece y las operaciones que se pueden efectuar son las mismas que las indicadas en el paso 5 del ejemplo 2.