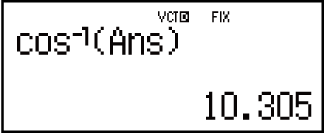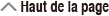Utilisez le Mode VECTOR pour effectuer des calculs vectoriels à 2 et 3 dimensions. Pour effectuer un calcul vectoriel, vous devez d'abord assigner des données aux variables spéciales de vecteur (VctA, VctB, VctC), et utiliser ensuite ces variables dans le calcul comme illustré dans l'exemple ci-dessous.

Exemple 1 : Assigner (1, 2) à VctA et (3, 4) à VctB, puis effectuer les calculs suivants : (1, 2) + (3, 4)

1. Appuyez sur (VECTOR) pour entrer dans le Mode VECTOR.

• 

2. Appuyez (VctA)(2).

• 

  (1) « A » signifie « VctA ».

3. Saisissez les éléments de VctA : 12.

4. Effectuez l'opération de touches suivante :
(VECTOR)(Data)(VctB)(2).

5. Saisissez les éléments de VctB : 34.

6. Appuyez sur pour avancer à l'écran de calcul et effectuez le calcul (VctA + VctB) :
(VECTOR)(VctA)(VECTOR)(VctB).

• (2) « Ans » signifie « VctAns ».

Mémoire de réponse de vecteur

À chaque fois que le résultat d'un calcul effectué en Mode VECTOR est un vecteur, l'écran VctAns apparaît avec le résultat. Le résultat est également assigné à une variable nommée « VctAns ».
La variable VctAns peut être utilisée dans les calculs comme décrit ci-dessous.

Pour insérer la variable VctAns dans un calcul, effectuez l'opération de touches suivante : (VECTOR)(VctAns).

Appuyer sur l'une des touches suivantes tandis que l'écran VctAns est affiché commute automatiquement à l'écran de calcul : , , , . L'écran de calcul affiche la variable VctAns suivie de l'opérateur ou de la fonction pour la touche que vous avez pressée.

Assigner et modifier les données de variable de vecteur

Pour assigner des nouvelles données à une variable de vecteur :

1. Appuyez sur (VECTOR)(Dim) puis, dans le menu qui apparaît, sélectionnez la variable de vecteur à laquelle vous souhaitez assigner les données.

2. Dans le menu suivant qui apparaît, sélectionnez les dimensions (m).

3. Utilisez l'éditeur de vecteur qui apparaît pour entrer les éléments du vecteur.

Exemple 2 : Assigner (2, -1, 2) à VctC

• (VECTOR)(Dim)(VctC)(3)
  212
• 

Pour modifier les éléments d'une variable de vecteur :

1. Appuyez sur (VECTOR)(Data) puis, dans le menu qui apparaît, sélectionnez la variable de vecteur que vous souhaitez modifier.

2. Utilisez l'éditeur de vecteur qui apparaît pour modifier les éléments du vecteur.
Déplacez le curseur à la cellule qui contient l'élément que vous voulez changer, entrez la nouvelle valeur, puis pressez .

Pour copier le contenu de la variable de vecteur (ou VctAns) :

1. Utilisez l'éditeur de vecteur pour afficher le vecteur que vous souhaitez copier.

2. Appuyez sur (STO) et effectuez ensuite l'une des opérations de touches suivantes pour spécifier la destination de la copie : (VctA), (VctB) ou (VctC).

Exemples de calcul vectoriel

Les exemples suivants utilisent VctA = (1, 2) et VctB = (3, 4) de l'exemple 1 et VctC = (2, -1, 2) de l'exemple 2.

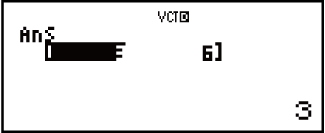
Exemple 3 : 3 × VctA (multiplication scalaire de vecteurs), 3 × VctA - VctB (exemple de calcul utilisant VctAns)

• 3(VECTOR)(VctA)
• 

• (VECTOR)(VctB)
• 

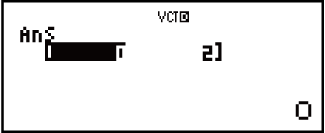
Exemple 4 : VctA • VctB (produit scalaire de vecteurs)

• (VECTOR)(VctA)
  (VECTOR)(Dot)
  (VECTOR)(VctB)
• 

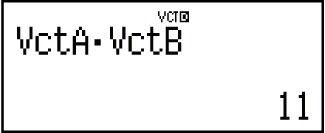
Exemple 5 : VctA × VctB (produit croisé de vecteurs)

• (VECTOR)(VctA)
  (VECTOR)(VctB)
• 

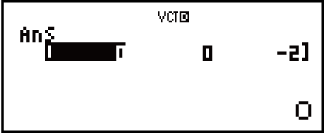
Exemple 6 : Obtenir les valeurs absolues de VctC.

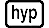• (Abs)
  (VECTOR)(VctC)
• 

Exemple 7 : Déterminer l'angle constitué par VctA et VctB avec trois décimales (Fix 3). (Unité d'angle : Deg)

(cos𝜃 = ^{(𝐴∙𝐵)} _|𝐴||𝐵|, qui devient 𝜃 = cos-1^{(𝐴∙𝐵)} _|𝐴||𝐵|)

• (SETUP)(Fix)
  (VECTOR)(VctA)
  (VECTOR)(Dot)
  (VECTOR)(VctB)
  (Abs)(VECTOR)(VctA)
  (Abs)(VECTOR)(VctB)
  
• 

• (cos-1)
•