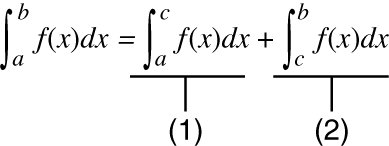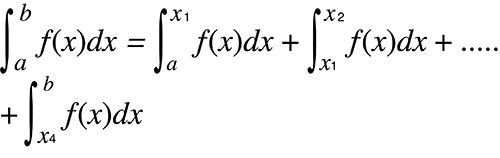Calculs intégrales
Fonction pour effectuer l'intégration numérique en utilisant la méthode de Gauss-Kronrod.
La syntaxe d'entrée en affichage Naturel est ∫ba f (x)dx, tandis que la syntaxe d'entrée en affichage Linéaire est ∫ (f (x), a, b, tol).
tol spécifie la tolérance, qui devient 1 × 10-5 quand rien n'est entré pour tol.
Exemple 1 : ∫e1 ln(x) = 1
(MthIO-MathO)

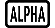
 (X)
(X)
 1
1
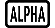
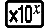 (e)
(e)
- 1
(LineIO)
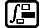

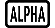
 (X)
(X)

 (,) 1
(,) 1
 (,)
(,)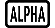
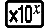 (e)
(e)

- 1
Exemple 2 : ∫(1x2 , 1, 5, 1 × 10-7) = 0,8 (LineIO)
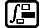 1
1
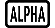
 (X)
(X)

 (,) 1
(,) 1
 (,) 5
(,) 5
 (,)
(,)
1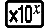
 7
7

- 0,8
Exemple 3 : ∫π0 (sin x + cos x)2 dx = π (tol : non spécifiée) (MthIO-MathO) (unité d'angle : Rad)
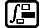


 (X)
(X)


 (X)
(X)


 0
0

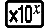 (π)
(π)
- π
Précautions de calculs d'intégrales
Les calculs d'intégrales peuvent être effectués dans le Mode COMP uniquement.
Ce qui suit ne peut pas être utilisé dans f(x) : Pol, Rec, ÷R. Ce qui suit ne peut pas être utilisé dans f(x), a, b, ou tol : ∫, d/dx, Σ, Π.
En utilisant une fonction trigonométrique dans f(x), spécifiez Rad comme unité d'angle.
Une plus petite valeur de tol augmente la précision, mais elle augmente également le temps de calcul. En spécifiant tol, utilisez une valeur qui est 1 × 10-14 ou plus grande.
L'intégration requiert normalement un temps d'exécution considérable.
Selon le contenu de f(x) et l'intervalle d'intégration, une erreur de calcul qui dépasse la tolérance peut être produite, provoquant l'affichage d'un message d'erreur.
Le contenu de f(x), des valeurs positives/négatives dans l'intervalle d'intégration, ainsi que l'intervalle à intégrer peuvent provoquer de grosses erreurs dans les valeurs d'intégration résultantes. (Exemples : des parties contenant des points discontinus ou un changement brusque. Lorsque l'intervalle d'intégration est trop large.) Dans ce type de cas, vous pouvez éventuellement améliorer la précision des calculs en divisant l'intervalle d'intégration en plusieurs parties, puis en effectuant le calcul.
Conseils pour la réussite des calculs d'intégrales
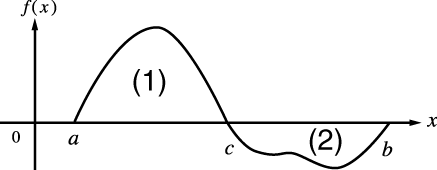
Quand une fonction périodique ou un intervalle d'intégration a pour résultat des valeurs positives et négatives de la fonction f(x)
Effectuez des intégrations séparées pour chaque cycle, ou pour la partie positive et la partie négative, puis combinez les résultats.
(1) Partie positive
(2) Partie négative
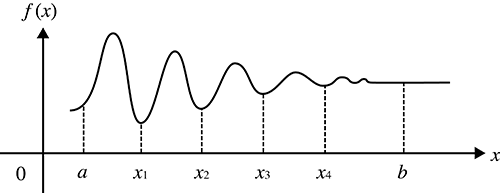
Quand les valeurs d'intégration varient largement en raison de minuscules variations dans l'intervalle d'intégration
Divisez l'intervalle d'intégration en plusieurs parties (d'une manière qui découpe les secteurs de larges fluctuations en petites parties), effectuez l'intégration sur chaque partie, puis combinez les résultats.