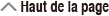Utilisation de SOLVE
SOLVE utilise la méthode de Newton pour approximer la résolution des équations.
Notez que SOLVE ne peut être utilisé que dans le Mode COMP.
Ce qui suit décrit les types d'équations dont les solutions peuvent être obtenues à l'aide de SOLVE.
Équations qui incluent la variable X : X2 + 2X - 2, Y = X + 5, X = sin(M), X + 3 = B + C
SOLVE résout pour X. Une expression comme X2 + 2X - 2 est traitée comme X2 + 2X - 2 = 0.
Entrée d'équations utilisant la syntaxe suivante : {équation}, {variable de solution}
SOLVE résout pour Y, par exemple, quand une équation est entrée comme : Y = X + 5, Y
Important !
Si une équation contient des fonctions d'entrée qui incluent une parenthèse ouverte (par exemple, sin et log), n'omettez pas la parenthèse fermante.
Les fonctions suivantes ne sont pas permises à l'intérieur d'une équation : ∫, d/dx, Σ, Π, Pol, Rec, ÷R.
Exemple : Résoudre y = ax2 + b pour x lorsque y = 0, a = 1 et b = -2
 (Y)
(Y)
 (=)
(=)
 (A)
(A)
 (X)
(X)

 (B)
(B)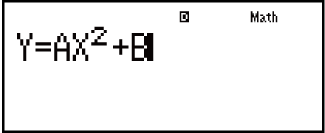

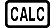 (SOLVE)
(SOLVE)
(1) Invite à entrer une valeur pour Y
(2) Valeur actuelle de Y
- 0
 1
1
 2
2
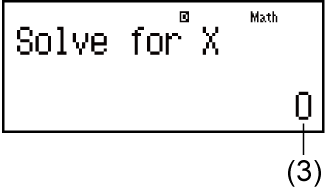
(3) Valeur actuelle de X
Saisissez une valeur initiale pour X (ici, saisissez 1) :
- 1

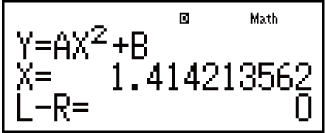
Écran de solution
- Pour quitter SOLVE :

Remarque
Pendant toute la période comprise entre le moment où vous appuyez sur 
 (SOLVE) jusqu'à la sortie de SOLVE en appuyant sur
(SOLVE) jusqu'à la sortie de SOLVE en appuyant sur  , vous devez utiliser les procédures de saisie de l'affichage Linéaire.
, vous devez utiliser les procédures de saisie de l'affichage Linéaire.
Important !
Selon ce que vous entrez pour la valeur initiale de X (variable de solution), SOLVE risque de ne pas pouvoir obtenir des solutions. Si ceci se produit, essayez de changer la valeur initiale pour qu'elle soit plus près de la solution.
SOLVE peut ne pas trouver la solution correcte, même si elle existe.
SOLVE utilise la méthode de Newton, si bien que même s'il y a plusieurs solutions, seulement l'une d'entre elles sera indiquée.
En raison des limitations de la méthode de Newton, les solutions tendent à être difficiles à obtenir pour des équations telles que les suivantes : y = sin(x), y = ex, y = √x.
Contenu de l'écran de solution
Les solutions sont toujours affichées sous forme décimale.

(1) Équation (l'équation que vous entrez.)
(2) Variable résolue pour
(3) Solution
(4) Résultat (côté gauche) - (côté droit)
« Résultat (côté gauche) - (côté droit) » donne le résultat quand le côté droit de l'équation est soustrait du côté gauche, après avoir assigné la valeur obtenue à la variable pour laquelle la solution est recherchée. Plus ce résultat est proche de zéro, plus la précision de la solution est élevée.
Écran continuer
SOLVE exécute la convergence un nombre de fois préréglé. S'il ne peut pas trouver de solution, il affiche un écran de confirmation qui comporte « Continue: [=] », demandant si vous voulez continuer.
Appuyez sur  pour continuer ou
pour continuer ou  pour annuler l'opération SOLVE.
pour annuler l'opération SOLVE.
Exemple : Résoudre y = x2 - x + 1 pour x quand y = 3, 7 et 13.
 (Y)
(Y)
 (=)
(=)
 (X)
(X)

 (X)
(X) 1
1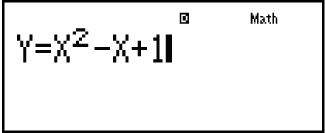

 (SOLVE)
(SOLVE)
- 3

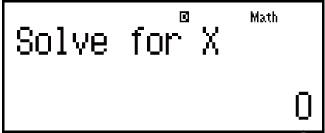
Saisissez une valeur initiale pour X (ici, saisissez 1) :
- 1

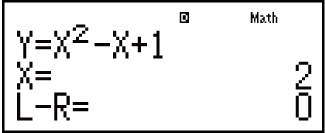
 7
7

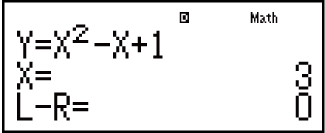
 13
13