Calculs différentiels
Fonction pour l'approximation de la dérivée basée sur la méthode de différence centrée.
La syntaxe d'entrée en affichage Naturel est ddx (f (x)) | x=a, tandis que la syntaxe d'entrée en affichage Linéaire est ddx (f (x), a, tol).
tol spécifie la tolérance, qui devient 1 × 10-10 quand rien n'est entré pour tol.
Exemple 1 : Déterminer la dérivée au point x = π/2 pour la fonction y = sin(x) (unité d'angle : Rad)
(MthIO-MathO)

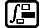 (
(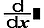 )
)
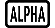
 (X)
(X)



 (π)
(π) 2
2
- 0
(LineIO)

 (
(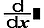 )
)
 (X)
(X)

 (,)
(,)
 (π)
(π) 2
2

- 0
Exemple 2 : ddx (3x2 - 5x + 2, 2, 1 × 10-12) = 7 (LineIO)

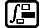 (
(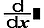 ) 3
) 3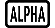
 (X)
(X)
 5
5
 (X)
(X) 2
2
 (,)
(,)
2
 (,) 1
(,) 1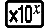
 12
12

- 7
Précautions de calculs différentiels
Le calcul différentiel peut être effectué dans le Mode COMP uniquement.
Ce qui suit ne peut pas être utilisé dans f(x) : Pol, Rec, ÷R. Ce qui suit ne peut pas être utilisé dans f(x), a, b, ou tol : ∫, d/dx, Σ, Π.
En utilisant une fonction trigonométrique dans f(x), spécifiez Rad comme unité d'angle.
Une plus petite valeur de tol augmente la précision, mais elle augmente également le temps de calcul. En spécifiant tol, utilisez une valeur qui est 1 × 10-14 ou plus grande.
Si la convergence vers une solution ne peut pas être trouvée quand l'entrée de tol est omise, la valeur de tol est ajustée automatiquement pour trouver une solution.
Des points non consécutifs, une fluctuation brusque, des points extrêmement grands ou petits, des points d'inflexion et l'inclusion de points qui ne peuvent pas être différenciés, ou un point différentiel ou le résultat d'un calcul différentiel qui approche zéro peuvent être la cause d'une erreur ou d'une mauvaise précision.