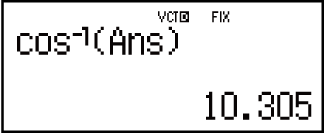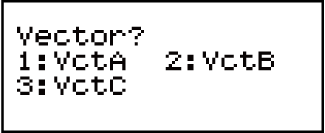fx-115ES PLUS
fx-991ES PLUS C
(2nd edition / NATURAL-V.P.A.M.)
Before Using the Calculator
Calculation Modes and Calculator Setup
Inputting Expressions and Values
- ▶Basic Input Rules
- ▶Inputting with Natural Display
- ▶√ Form Calculation Range
- ▶Using Values and Expressions as Arguments (Natural Display only)
- ▶Overwrite Input Mode (Linear Display only)
- ▶Correcting and Clearing an Expression
Basic Calculations
- ▶Toggling Calculation Results
- ▶Fraction Calculations
- ▶Percent Calculations
- ▶Degree, Minute, Second (Sexagesimal) Calculations
- ▶Multi-Statements
- ▶Using Engineering Notation
- ▶Remainder Calculations
- ▶Recurring Decimal Calculations
- ▶Prime Factorization
- ▶Calculation History and Replay
- ▶Using Memory Functions
Function Calculations
- ▶Pi (π), Natural Logarithm Base e
- ▶Trigonometric Functions
- ▶Hyperbolic Functions
- ▶Angle Unit Conversion
- ▶Exponential Functions
- ▶Logarithmic Functions
- ▶Power Functions and Power Root Functions
- ▶Integration Calculations
- ▶Differential Calculations
- ▶Σ Calculations
- ▶Π Calculations
- ▶Rectangular-Polar Coordinate Conversion
- ▶Factorial Function (!)
- ▶Absolute Value Function (Abs)
- ▶Random Number (Ran#)
- ▶Random Integer (RanInt#)
- ▶Permutation (nPr) and Combination (nCr)
- ▶Rounding Function (Rnd)
- ▶Greatest Common Divisor (GCD) and Least Common Multiple (LCM)
- ▶Integer Part of a Value (Int) and Largest Integer that does not Exceed a Value (Intg)
- ▶Using CALC
- ▶Using SOLVE
- ▶Scientific Constants
- ▶Metric Conversion
Using Calculation Modes
- ▶Complex Number Calculations (CMPLX)
- ▶Statistical Calculations (STAT)
- ▶Base-n Calculations (BASE-N)
- ▶Equation Calculations (EQN)
- ▶Matrix Calculations (MATRIX)
- ▶Creating a Numerical Table from Two Functions (TABLE)
- ▶Vector Calculations (VECTOR)
- ▶Inequality Calculations (INEQ)
- ▶Using VERIFY (VERIF)
- ▶Distribution Calculations (DIST)
Technical Information
- ▶Errors
- ▶Before Assuming Malfunction of the Calculator...
- ▶Replacing the Battery
- ▶Calculation Priority Sequence
- ▶Calculation Ranges, Number of Digits, and Precision
- ▶Specifications
- ▶Verifying the Authenticity of Your Calculator
Frequently Asked Questions
Vector Calculations (VECTOR)
Use the VECTOR Mode to perform 2-dimensional and 3-dimensional vector calculations. To perform a vector calculation, you first assign data to special vector variables (VctA, VctB, VctC), and then use the variables in the calculation as shown in the example below.
Example 1: To assign (1, 2) to VctA and (3, 4) to VctB, and then perform the following calculations: (1, 2) + (3, 4)
1. Press 
 (VECTOR) to enter the VECTOR Mode.
(VECTOR) to enter the VECTOR Mode.
2. Press  (VctA)
(VctA) (2).
(2).
This will display the Vector Editor for input of the 2-dimensional vector for VctA.

(1) "A" stands for "VctA".
3. Input the elements of VctA: 1 2
2 .
.
4. Perform the following key operation:

 (VECTOR)
(VECTOR) (Data)
(Data) (VctB)
(VctB) (2).
(2).
This will display the Vector Editor for input of the 2-dimensional vector for VctB.
5. Input the elements of VctB: 3 4
4 .
.
6. Press  to advance to the calculation screen, and perform the calculation (VctA+VctB):
to advance to the calculation screen, and perform the calculation (VctA+VctB):

 (VECTOR)
(VECTOR) (VctA)
(VctA)

 (VECTOR)
(VECTOR) (VctB)
(VctB) .
.
This will display the VctAns screen with the calculation results.

- (2) "Ans" stands for "VctAns".
Note: "VctAns" stands for "Vector Answer Memory". See "Vector Answer Memory" for more information.
Vector Answer Memory
Whenever the result of a calculation executed in the VECTOR Mode is a vector, the VctAns screen will appear with the result. The result also will be assigned to a variable named "VctAns".
The VctAns variable can be used in calculations as described below.
To insert the VctAns variable into a calculation, perform the following key operation: 
 (VECTOR)
(VECTOR) (VctAns).
(VctAns).
Pressing any one of the following keys while the VctAns screen is displayed will switch automatically to the calculation screen:  ,
,  ,
,  ,
,  . The calculation screen will show the VctAns variable followed by the operator or function for the key you pressed.
. The calculation screen will show the VctAns variable followed by the operator or function for the key you pressed.
Assigning and Editing Vector Variable Data
Important!
The following operations are not supported by the Vector Editor:  ,
, 
 (M-),
(M-), 
 (STO). Pol, Rec, ÷R, and multi-statements also cannot be input with the Vector Editor.
(STO). Pol, Rec, ÷R, and multi-statements also cannot be input with the Vector Editor.
To assign new data to a vector variable:
1. Press 
 (VECTOR)
(VECTOR) (Dim), and then, on the menu that appears, select the vector variable to which you want to assign data.
(Dim), and then, on the menu that appears, select the vector variable to which you want to assign data.
2. On the next menu that appears, select dimension (m).
3. Use the Vector Editor that appears to input the elements of the vector.
Example 2: To assign (2, -1, 2) to VctC

 (VECTOR)
(VECTOR) (Dim)
(Dim) (VctC)
(VctC) (3)
(3)
2
 1
1 2
2

To edit the elements of a vector variable:
1. Press 
 (VECTOR)
(VECTOR) (Data), and then, on the menu that appears, select the vector variable you want to edit.
(Data), and then, on the menu that appears, select the vector variable you want to edit.
2. Use the Vector Editor that appears to edit the elements of the vector.
Move the cursor to the cell that contains the element you want to change, input the new value, and then press  .
.
To copy vector variable (or VctAns) contents:
1. Use the Vector Editor to display the vector you want to copy.
If you want to copy VctA, for example, perform the following key operation: 
 (VECTOR)
(VECTOR) (Data)
(Data) (VctA).
(VctA).
If you want to copy VctAns contents, perform the following to display the VctAns screen: 

 (VECTOR)
(VECTOR) (VctAns)
(VctAns) .
.
2. Press 
 (STO), and then perform one of the following key operations to specify the copy destination:
(STO), and then perform one of the following key operations to specify the copy destination:  (VctA),
(VctA),  (VctB), or
(VctB), or  (VctC).
(VctC).
This will display the Vector Editor with the contents of the copy destination.
Vector Calculation Examples
The following examples use VctA = (1, 2) and VctB = (3, 4) from Example 1, and VctC = (2, -1, 2) from Example 2.
Example 3: 3 × VctA (Vector scalar multiplication), 3 × VctA - VctB (Calculation example using VctAns)
 3
3

 (VECTOR)
(VECTOR) (VctA)
(VctA)
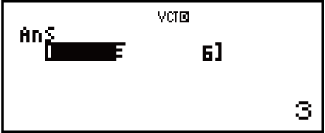


 (VECTOR)
(VECTOR) (VctB)
(VctB)
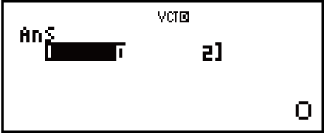
Example 4: VctA • VctB (Vector dot product)


 (VECTOR)
(VECTOR) (VctA)
(VctA)

 (VECTOR)
(VECTOR) (Dot)
(Dot)

 (VECTOR)
(VECTOR) (VctB)
(VctB)
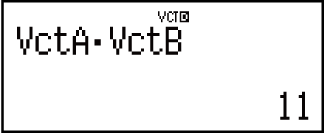
Example 5: VctA × VctB (Vector cross product)


 (VECTOR)
(VECTOR) (VctA)
(VctA)

 (VECTOR)
(VECTOR) (VctB)
(VctB)
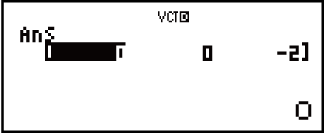
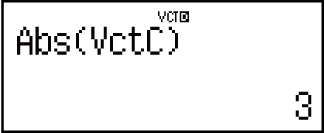
Example 6: Obtain the absolute values of VctC.


 (Abs)
(Abs)

 (VECTOR)
(VECTOR) (VctC)
(VctC)

Example 7: Determine the angle formed by VctA and VctB to three decimal places (Fix 3). (Angle unit: Deg)
(cos𝜃 = (𝐴∙𝐵) |𝐴||𝐵|, which becomes 𝜃 = cos-1(𝐴∙𝐵) |𝐴||𝐵|)

 (SETUP)
(SETUP) (Fix)
(Fix)



 (VECTOR)
(VECTOR) (VctA)
(VctA)

 (VECTOR)
(VECTOR) (Dot)
(Dot)

 (VECTOR)
(VECTOR) (VctB)
(VctB)



 (Abs)
(Abs)
 (VECTOR)
(VECTOR) (VctA)
(VctA)


 (Abs)
(Abs)
 (VECTOR)
(VECTOR) (VctB)
(VctB)





 (cos-1)
(cos-1)