Remainder Calculations

You can use the ÷R function to obtain the quotient and remainder in a division calculation.

Example: To calculate the quotient and remainder of 5 ÷ 2 (quotient = 2, remainder = 1)

(MthIO-MathO)
5(÷R) 2

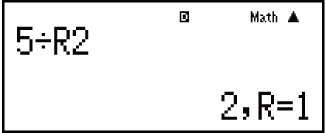
(LineIO)
5(÷R) 2

Note

Only the quotient value of a ÷R calculation is stored in Ans memory.

Assigning the result of a remainder division calculation to a variable will assign the quotient value only. Performing the operation 5(÷R) 2(STO)(X) (which assigns the result of 5÷R2 to X) will assign a value of 2 to X.

If a ÷R calculation is part of a multi-step calculation, only the quotient is passed on to the next operation.
Example: 1017(÷R) 6 → 102 → 12

Operation of the and keys is disabled while a remainder division result is on the display.

Cases when Remainder Division becomes Non-remainder Division

If either of the conditions below exists when you perform a remainder division operation, the calculation will be treated as normal (non-remainder) division.

When either the dividend or the divisor is a very large value
Example: 20000000000(÷R) 17

→ Calculated as: 20000000000 ÷ 17

When the quotient is not a positive integer, or if the remainder is not a positive integer or positive fractional value
Example: 5(÷R) 2 → Calculated as: -5 ÷ 2