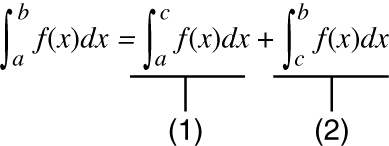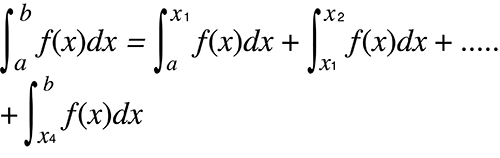fx-115ES PLUS
fx-991ES PLUS C
(2nd edition / NATURAL-V.P.A.M.)
Before Using the Calculator
Calculation Modes and Calculator Setup
Inputting Expressions and Values
- ▶Basic Input Rules
- ▶Inputting with Natural Display
- ▶√ Form Calculation Range
- ▶Using Values and Expressions as Arguments (Natural Display only)
- ▶Overwrite Input Mode (Linear Display only)
- ▶Correcting and Clearing an Expression
Basic Calculations
- ▶Toggling Calculation Results
- ▶Fraction Calculations
- ▶Percent Calculations
- ▶Degree, Minute, Second (Sexagesimal) Calculations
- ▶Multi-Statements
- ▶Using Engineering Notation
- ▶Remainder Calculations
- ▶Recurring Decimal Calculations
- ▶Prime Factorization
- ▶Calculation History and Replay
- ▶Using Memory Functions
Function Calculations
- ▶Pi (π), Natural Logarithm Base e
- ▶Trigonometric Functions
- ▶Hyperbolic Functions
- ▶Angle Unit Conversion
- ▶Exponential Functions
- ▶Logarithmic Functions
- ▶Power Functions and Power Root Functions
- ▶Integration Calculations
- ▶Differential Calculations
- ▶Σ Calculations
- ▶Π Calculations
- ▶Rectangular-Polar Coordinate Conversion
- ▶Factorial Function (!)
- ▶Absolute Value Function (Abs)
- ▶Random Number (Ran#)
- ▶Random Integer (RanInt#)
- ▶Permutation (nPr) and Combination (nCr)
- ▶Rounding Function (Rnd)
- ▶Greatest Common Divisor (GCD) and Least Common Multiple (LCM)
- ▶Integer Part of a Value (Int) and Largest Integer that does not Exceed a Value (Intg)
- ▶Using CALC
- ▶Using SOLVE
- ▶Scientific Constants
- ▶Metric Conversion
Using Calculation Modes
- ▶Complex Number Calculations (CMPLX)
- ▶Statistical Calculations (STAT)
- ▶Base-n Calculations (BASE-N)
- ▶Equation Calculations (EQN)
- ▶Matrix Calculations (MATRIX)
- ▶Creating a Numerical Table from Two Functions (TABLE)
- ▶Vector Calculations (VECTOR)
- ▶Inequality Calculations (INEQ)
- ▶Using VERIFY (VERIF)
- ▶Distribution Calculations (DIST)
Technical Information
- ▶Errors
- ▶Before Assuming Malfunction of the Calculator...
- ▶Replacing the Battery
- ▶Calculation Priority Sequence
- ▶Calculation Ranges, Number of Digits, and Precision
- ▶Specifications
- ▶Verifying the Authenticity of Your Calculator
Frequently Asked Questions
Integration Calculations
Function for performing numerical integration using the Gauss-Kronrod method.
Natural Display input syntax is ∫ba f (x)dx, while Linear Display input syntax is ∫ (f (x), a, b, tol).
tol specifies tolerance, which becomes 1 × 10-5 when nothing is input for tol.
Example 1: ∫e1 ln(x) = 1
(MthIO-MathO)


 (X)
(X)
 1
1

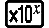 (e)
(e)
- 1
(LineIO)


 (X)
(X)
 (,) 1
(,) 1
 (,)
(,)
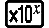 (e)
(e)

- 1
Example 2: ∫(1x2 , 1, 5, 1 × 10-7) = 0.8 (LineIO)
 1
1

 (X)
(X)
 (,) 1
(,) 1
 (,) 5
(,) 5
 (,)
(,)
1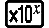
 7
7

- 0.8
Example 3: ∫π0 (sin x + cos x)2 dx = π (tol: Not specified) (MthIO-MathO) (Angle unit: Rad)



 (X)
(X)



 (X)
(X)


 0
0
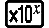 (π)
(π)
- π
Integration Calculation Precautions
Integration calculation can be performed in the COMP Mode only.
The following cannot be used in f(x): Pol, Rec, ÷R. The following cannot be used in f(x), a, b, or tol: ∫, d/dx, Σ, Π.
When using a trigonometric function in f(x), specify Rad as the angle unit.
A smaller tol value increases precision, but it also increases calculation time. When specifying tol, use value that is 1 × 10-14 or greater.
Integration normally requires considerable time to perform.
Depending on the content of f(x) and the region of integration, calculation error that exceeds the tolerance may be generated, causing the calculator to display an error message.
The content of f(x), positive/negative values within the integration interval, and the interval to be integrated can cause large error in the resulting integration values. (Examples: When there are parts with discontinuous points or abrupt change. When the integration interval is too wide.) In such cases dividing the integration interval into parts and performing the calculation may improve calculation accuracy.
Tips for Successful Integration Calculations
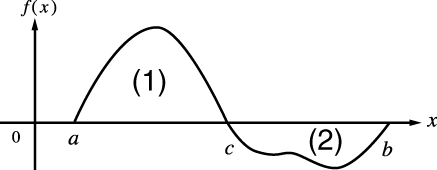
When a periodic function or integration interval results in positive and negative f(x) function values
Perform separate integrations for each cycle, or for the positive part and the negative part, and then combine the results.
(1) Positive Part
(2) Negative Part
When integration values fluctuate widely due to minute shifts in the integration interval
Divide the integration interval into multiple parts (in a way that breaks areas of wide fluctuation into small parts), perform integration on each part, and then combine the results.