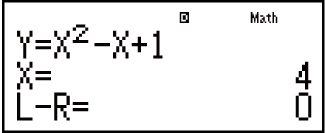fx-115ES PLUS
fx-991ES PLUS C
(2nd edition / NATURAL-V.P.A.M.)
Before Using the Calculator
Calculation Modes and Calculator Setup
Inputting Expressions and Values
- ▶Basic Input Rules
- ▶Inputting with Natural Display
- ▶√ Form Calculation Range
- ▶Using Values and Expressions as Arguments (Natural Display only)
- ▶Overwrite Input Mode (Linear Display only)
- ▶Correcting and Clearing an Expression
Basic Calculations
- ▶Toggling Calculation Results
- ▶Fraction Calculations
- ▶Percent Calculations
- ▶Degree, Minute, Second (Sexagesimal) Calculations
- ▶Multi-Statements
- ▶Using Engineering Notation
- ▶Remainder Calculations
- ▶Recurring Decimal Calculations
- ▶Prime Factorization
- ▶Calculation History and Replay
- ▶Using Memory Functions
Function Calculations
- ▶Pi (π), Natural Logarithm Base e
- ▶Trigonometric Functions
- ▶Hyperbolic Functions
- ▶Angle Unit Conversion
- ▶Exponential Functions
- ▶Logarithmic Functions
- ▶Power Functions and Power Root Functions
- ▶Integration Calculations
- ▶Differential Calculations
- ▶Σ Calculations
- ▶Π Calculations
- ▶Rectangular-Polar Coordinate Conversion
- ▶Factorial Function (!)
- ▶Absolute Value Function (Abs)
- ▶Random Number (Ran#)
- ▶Random Integer (RanInt#)
- ▶Permutation (nPr) and Combination (nCr)
- ▶Rounding Function (Rnd)
- ▶Greatest Common Divisor (GCD) and Least Common Multiple (LCM)
- ▶Integer Part of a Value (Int) and Largest Integer that does not Exceed a Value (Intg)
- ▶Using CALC
- ▶Using SOLVE
- ▶Scientific Constants
- ▶Metric Conversion
Using Calculation Modes
- ▶Complex Number Calculations (CMPLX)
- ▶Statistical Calculations (STAT)
- ▶Base-n Calculations (BASE-N)
- ▶Equation Calculations (EQN)
- ▶Matrix Calculations (MATRIX)
- ▶Creating a Numerical Table from Two Functions (TABLE)
- ▶Vector Calculations (VECTOR)
- ▶Inequality Calculations (INEQ)
- ▶Using VERIFY (VERIF)
- ▶Distribution Calculations (DIST)
Technical Information
- ▶Errors
- ▶Before Assuming Malfunction of the Calculator...
- ▶Replacing the Battery
- ▶Calculation Priority Sequence
- ▶Calculation Ranges, Number of Digits, and Precision
- ▶Specifications
- ▶Verifying the Authenticity of Your Calculator
Frequently Asked Questions
Using SOLVE
SOLVE uses Newton's method to approximate the solution of equations.
Note that SOLVE can be used in the COMP Mode only.
The following describes the types of equations whose solutions can be obtained using SOLVE.
Equations that include variable X: X2 + 2X - 2, Y = X + 5, X = sin(M), X + 3 = B + C
SOLVE solves for X. An expression like X2 + 2X - 2 is treated as X2 + 2X - 2 = 0.
Equations input using the following syntax: {equation}, {solution variable}
SOLVE solves for Y, for example, when an equation is input as: Y = X +
5, Y
Important!
If an equation contains input functions that include an open parenthesis (such as sin and log), do not omit the closing parenthesis.
The following functions are not allowed inside of an equation: ∫, d/dx, Σ, Π, Pol, Rec, ÷R.
Example: To solve y = ax2 + b for x when y = 0, a = 1, and b = -2

 (Y)
(Y)
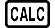 (=)
(=)

 (A)
(A)
 (X)
(X)


 (B)
(B)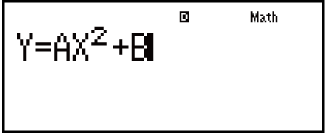
 (SOLVE)
(SOLVE)
-
(1) Prompts for input of a value for Y
(2) Current value of Y
- 0
 1
1
 2
2
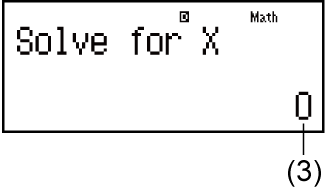
-
(3) Current value of X
Input an initial value for X (Here, input 1):
- 1


Solution Screen
- To exit SOLVE:

Note
During the time from when you press 
 (SOLVE) until you exit
SOLVE by pressing
(SOLVE) until you exit
SOLVE by pressing  , you should use Linear Display input procedures for input.
, you should use Linear Display input procedures for input.
Important!
Depending on what you input for the initial value for X (solution variable), SOLVE may not be able to obtain solutions. If this happens, try changing the initial value so they are closer to the solution.
SOLVE may not be able to determine the correct solution, even when one exists.
SOLVE uses Newton's method, so even if there are multiple solutions, only one of them will be returned.
Due to limitations in Newton's method, solutions tend to be difficult to obtain for equations like the following: y = sin(x), y = ex, y = √x.
Solution Screen Contents
Solutions are always displayed in decimal form.

(1) Equation (The equation you input.)
(2) Variable solved for
(3) Solution
(4) (Left Side) - (Right Side) result
"(Left Side) - (Right Side) result" shows the result when the right side of the equation is subtracted from the left side, after assigning the obtained value to the variable being solved for. The closer this result is to zero, the higher the accuracy of the solution.
Continue Screen
SOLVE performs convergence a preset number of times. If it cannot find a solution, it displays a confirmation screen that shows "Continue: [=]", asking if you want to continue.
Press  to continue or
to continue or  to cancel the SOLVE operation.
to cancel the SOLVE operation.
Example: To solve y = x2 - x + 1 for x when y = 3, 7, and 13.

 (Y)
(Y)
 (=)
(=)

 (X)
(X)


 (X)
(X) 1
1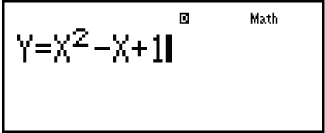
 (SOLVE)
(SOLVE)
- 3

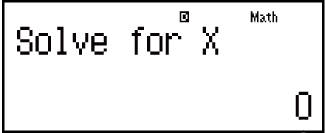
Input an initial value for X (Here, input 1):
- 1

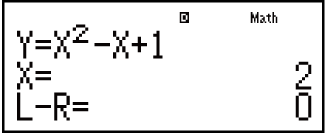
 7
7

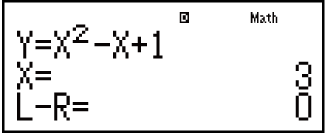
 13
13