Détails du menu Catalogue

Le menu Catalogue, qui s’affiche lorsque vous appuyez sur C, est une liste complète de toutes les fonctions, commandes, variables d’application^* et symboles disponibles sur la calculatrice. Vous pouvez sélectionner l’élément souhaité sur la calculatrice et l’entrer dans un calcul ou une expression.

La liste établie par C > [Tout] contient tous les éléments pris en charge par votre calculatrice. Lorsque la liste alphabétique est affichée, vous pouvez appuyer sur une touche de X^A à 0^Z pour passer au début de la liste pour la lettre dont vous avez appuyé sur la touche. Sélectionnez une lettre de [A] à [Z], puis appuyez sur O pour afficher une liste d’éléments commençant par la lettre sélectionnée.

Les fonctions et les symboles qui ne sont pas inclus dans un groupe de [A] à [Z] sont accessibles avec C > [Tout] > [Symboles].

Éléments inclus dans C > [Données variables] (variables d’entrée/sortie utilisées dans une application)

Remarque

Le fait d’appuyer sur C pendant l’utilisation de l’application Python ou de l’application Base-N affiche un menu Catalogue spécifique à chaque application. Pour plus de détails, consultez les chapitres expliquant chaque application.

Le menu Catalogue affiche les noms des fonctions et des commandes dans les menus par catégorie (comme Intégrale (∫), etc.). Dans les menus C > [Tout] et Historique des saisies, les fonctions et les commandes sont affichées dans la syntaxe de saisie des lignes (comme ∫(,,), etc.).

Utiliser l’historique des saisies

Jusqu’à 10 des dernières fonctions et commandes^* récemment saisies dans le menu Catalogue sont conservées en tant qu’historique des saisies. Pour consulter l’historique des saisies, sélectionnez C > [Historique].

Y compris l’historique des saisies épinglées.

Épinglage de l’historique des saisies

Lorsque vous consultez l’historique des saisies, sélectionnez l’élément que vous souhaitez brocher, puis appuyez sur T. Une broche s’affiche alors à gauche de l’élément.

La prochaine fois que vous ouvrirez l’historique des saisies, l’élément broché sera en haut de la liste.

Pour désépingler un élément, sélectionnez l’élément que vous souhaitez désépingler et appuyez sur T.

Liste des éléments regroupés par catégorie

Remarquez les points suivants concernant la syntaxe des fonctions et des commandes, à l’exception de celles de la catégorie Conversions d’unité.

Si la syntaxe de saisie naturelle et la syntaxe de saisie de ligne sont différentes pour une fonction, la syntaxe de saisie naturelle est affichée en premier, suivie de la syntaxe de saisie de ligne.

Tout ce qui est facultatif dans une syntaxe est placé entre crochets ([ ]). Avec la syntaxe $∫ (f (x), a, b [, t o l])$ , l’argument $t o l$ peut être omis, ce qui donne $∫ (f (x), a, b)$ .

Étude de fonction

Dérivée (d/dx) d/dx(,)

Utilise un calcul approximatif pour déterminer le coefficient différentiel du premier ordre de $f (x)$ à $x = a$ .

Syntaxe : $\frac{d}{d x} (f (x)) |_{x = a}$ $d / d x (f (x), a)$

Non autorisé dans cette syntaxe : $d / d x$ , $d^{2} / d x^{2}$ , $∫ d x$ , Σ, FMin, FMax, Solve, RndFix

Exemple : $\frac{d}{d x} (f (x^{3} + 4 x^{2} + x - 6)) |_{x = 3} = 52$

Précautions

Lorsque $f (x)$ est une fonction trigonométrique, veillez à sélectionner l’unité d’angle suivante : S > [Angle] > [Radians].

Les résultats inexacts et les erreurs peuvent être causés par l’un des éléments suivants :

Points discontinus dans les valeurs $x$

Variations extrêmes des valeurs $x$

Inclusion du point maximum local et du point minimum local dans les valeurs de $x$

L’inclusion du point d’inflexion dans les valeurs de $x$

Inclusion de points indifférenciables dans les valeurs de $x$

Résultats des calculs proches de zéro

Dérivée 2de (d²/dx²) d²/dx²(,)

Utilise un calcul approximatif pour déterminer le coefficient différentiel du second ordre de $f (x)$ à $x = a$ .

Syntaxe : $\frac{d^{2}}{{d x}^{2}} (f (x)) |_{x = a}$ $d^{2} / {d x}^{2} (f (x), a)$

Les éléments qui ne sont pas autorisés dans cette syntaxe et les précautions à prendre sont les mêmes que pour $d / d x$ .

Intégrale (∫) ∫(,,)

Utilise un calcul approximatif pour déterminer l’intégrale de $f (x)$ à $a$ ≤ $x$ ≤ $b$ . Cette fonction renvoie une valeur positive lorsque $f (x)$ est dans la plage positive et une valeur négative lorsque $f (x)$ est dans la plage négative. (Exemple : $∫_{2}^{3} x^{2} - 4 d x = \frac{7}{3}$ ; $∫_{1}^{2} x^{2} - 4 d x = - \frac{5}{3}$ ).

Syntaxe : $∫_{a}^{b} f (x) d x$ $∫ (f (x), a, b [, t o l])$

Pour $t o l$ , saisissez la plage d’erreur (tolérance) autorisée. Par défaut : 1 × 10^-5 si omis et pour les saisies naturelles.

Non autorisé dans cette syntaxe : $d / d x$ , $d^{2} / d x^{2}$ , $∫ d x$ , Σ, FMin, FMax, Solve, RndFix

Exemple : $∫_{1}^{5} {2 x}^{2} + 3 x + 4 d x = \frac{404}{3}$

Précautions

Lorsque $f (x)$ est une fonction trigonométrique, veillez à sélectionner l’unité d’angle suivante : S > [Angle] > [Radians].

L’intégration numérique étant utilisée, les valeurs d’intégration calculées peuvent être entachées d’une erreur importante due au contenu de $f (x)$ , aux valeurs positives et négatives dans l’intervalle d’intégration ou à l’intervalle en cours d’intégration. (Exemple : Lorsque des parties comportent des points discontinus ou des modifications brusques. Lorsque l’intervalle d’intégration est trop grand.) Le cas échéant, le fait de diviser l’intervalle d’intégration en plusieurs parties, puis d’effectuer les calculs, peut améliorer la précision des calculs.

Somme (Σ) Σ(,,,)

Obtient la somme pour une plage spécifiée de $f (x)$ .

Syntaxe : $\sum_{x = a}^{b} (f (x))$ $\sum (f (x), x, a, b [, n])$ $a$ , $b$ , $n$ = entiers, $a$ < $b$

$x$ peut être n’importe quelle variable alphabétique. $n$ spécifie l’intervalle du pas. Par défaut : 1 si omis et pour une saisie naturelle.

Non autorisé dans cette syntaxe : $d / d x$ , $d^{2} / d x^{2}$ , $∫ d x$ , Σ, FMin, FMax, Solve, RndFix

Exemple : $\sum_{x = 2}^{6} (x^{2} - 3 x + 5) = 55$

Résoudre équation (SolveN) SolveN()

Obtient plusieurs solutions d’une équation.

Syntaxe : SolveN( $f (x)$ [= côté droit] [, $x$ ] [,limite inférieure,limite supérieure])

Si [=côté droit] est omis, $f (x)$ = la valeur 0 est présumée. Spécifiez une Variable alphabétique quelconque pour les [ $, x$ ] et utilisez la même variable pour $f (x)$ . Si [, $x$ ] est omis, la variable $x$ est utilisée.

Jusqu’à 10 solutions sont renvoyées sous forme de liste.

« Aucune solution » est renvoyé si aucune solution n’existe.

S’il existe une solution autre que celle ou celles proposées, le message « Plusieurs solutions » s’affiche sur l’écran.

Non autorisé dans cette syntaxe : $d^{2} / d x^{2}$ , Σ, FMin, FMax, Solve

Exemple : SolveN $(x^{2} - 5 x - 6) = {- 1, 6}$

Trouver 1 solution (Solve) Solve(,)

Approche d’une solution unique pour $f (x)$ = 0. Cette fonction a les mêmes fonctionnalités que Utilisation de Solveur de l’application Équations.

Syntaxe : Solve( $f (x)$ ,estimation initiale [,limite inférieure,limite supérieure])

Non autorisé dans cette syntaxe : $d^{2} / d x^{2}$ , Σ, FMin, FMax, Solve

Div. Euclidienne, Reste Rmdr

Permet d’obtenir le reste lorsqu’un nombre entier est divisé par un autre nombre entier.

Syntaxe : dividende Rmdr diviseur

Exemple : 17 Rmdr 7 = 3

Div. Euclidienne, Quotient Int÷

Permet d’obtenir le quotient d’un nombre entier divisé par un autre nombre entier.

Syntaxe : dividende Int÷ diviseur

Exemple : 17 Int÷ 7 = 2

Simplification ISimp

Réduit une fraction à ses termes les plus petits. Avec l’application Calculs, utilisez les réglages ci-dessous.

S > [Simplifier] > [Manuel]

S > [Forme complexe] > [Réels]

Utilisez l’une des syntaxes ci-dessous pour ISimp.

Syntaxe 1 : FractionISimp

Réduit automatiquement la fraction dans l’argument en la divisant par le plus petit nombre premier divisible. Le nombre premier et le résultat de la réduction sont affichés sur l’écran.

Syntaxe 2 : FractionISimp $n$

Divise la fraction dans l’argument par le diviseur spécifié par $n$ . Le résultat de la division est affiché sur l’écran.

Exemple 1 : $\frac{15}{60} = \frac{5}{20} = \frac{1}{4}$

15e60r
C > [Étude de fonction] > [Simplification]E

CY875_Function Analysis_Simplification_1

C > [Historique] > [ISimp]E

CY875_Function Analysis_Simplification_2

Exemple 2 : $\frac{15}{60} = \frac{3}{12}$ (Spécifie un diviseur de 5.)

15e60r
C > [Étude de fonction] > [Simplification]5E

CY875_Function Analysis_Simplification_3

Précautions

Lorsque vous sélectionnez [a+b $i$ ] ou [r∠θ] pour S > [Forme complexe], les résultats des calculs de fraction sont toujours simplifiés avant d’être affichés, même si S > [Simplifier] est réglé sur [Manuel].

Valeur min fonct FMin(,,)

Renvoie, sous forme de liste, les coordonnées des valeurs minimales de $f (x)$ à $a$ ≤ $x$ ≤ $b$ .

Syntaxe : FMin( $f (x)$ , $a$ , $b$ [, $n$ ]) $n$ : Précision des calculs ( $n$ = nombre entier de 1 à 9)

Non autorisé dans cette syntaxe : $d / d x$ , $d^{2} / d x^{2}$ , $∫ d x$ , Σ, FMin, FMax, Solve, RndFix

Exemple : FMin( $x^{2}$ ,-2,1) = {0,0}

Précautions

Des points discontinus ou des sections présentant des fluctuations importantes peuvent nuire à la précision ou provoquer une erreur.

Saisir une valeur plus importante pour $n$ augmente la précision du calcul, mais aussi le temps nécessaire pour effectuer le calcul.

Valeur max fonct FMax(,,)

Renvoie, sous forme de liste, les coordonnées des valeurs maximales de $f (x)$ à $a$ ≤ $x$ ≤ $b$ .

Syntaxe : FMax( $f (x)$ , $a$ , $b$ [, $n$ ]) $n$ : Précision des calculs ( $n$ = nombre entier de 1 à 9)

Les éléments qui ne sont pas autorisés dans cette syntaxe et les précautions à prendre sont les mêmes que pour FMin.

Logarithme (logab) logab(,)

Obtient le logarithme de $b$ en base $a$ .

Syntaxe : $\log_{a} (b)$ log( $a$ , $b$ )

Logarithme (log) log()

Obtient le logarithme décimal de $a$ (logarithme de base 10).

Syntaxe : log( $a$ )

Logarithme népérien (ln) ln()

Obtient le logarithme naturel de $a$ .

Syntaxe : ln( $a$ )

Probabilités

Factorielle (!) !

Obtient la factorielle de 0 ou d’un entier positif.

Syntaxe : $n!$ $n$ = entier

Permutation (P) P

Obtient le nombre total de permutations $r$ prises dans l’ensemble $n$ .

Syntaxe : $n$ P $r$ $n$ , $r$ = entiers

Combinaison (C) C

Obtient le nombre total de combinaisons $r$ prises dans l’ensemble $n$ .

Syntaxe : $n$ C $r$ $n$ , $r$ = entiers

Nombre aléatoire (0 à 1) Ran#

Chaque exécution renvoie un nombre aléatoire de 10 chiffres (de 0 à 1).

Syntaxe : Ran# [ $a$ ] 1 ≤ $a$ ≤ 9 ( $a$ = entier)

$a$ : Spécifie la séquence de nombres aléatoires. S’il est omis, un nombre aléatoire vrai est renvoyé. S’il est spécifié, la séquence de nombres aléatoires de la calculatrice correspondante est invoquée et un nombre aléatoire fixe est renvoyé. Par exemple, l’exécution de Ran# 1 après l’initialisation des séquences^* renvoie toujours des nombres aléatoires de la séquence 1 dans l’ordre (0,701320948, 0,9297706456, 0,2939058016, ...)

Pour initialiser les séquences, exécutez Ran# 0. Cela permet également d’initialiser les séquences dans RanList#. Les séquences peuvent également être initialisées en utilisant Ran# ou RanList# pour générer une série de nombres aléatoires différente de la dernière série exécutée ou en générant un véritable nombre aléatoire.

Entier aléatoire (n à m) RanInt#(,)

Génère un nombre entier aléatoire entre deux nombres entiers spécifiés, $n$ et $m$ .

Syntaxe : RanInt#( $n$ , $m$ [, $a$ ]) $n$ < $m$ , | $n$ | < 1×10¹⁰, | $m$ | < 1×10¹⁰, $m$ ‒ $n$ < 1×10¹⁰, 1 ≤ $a$ ≤ 999

$a$ : Spécifie le nombre de nombres aléatoires. S’il est omis, un nombre aléatoire est renvoyé. Si spécifié, renvoie le nombre spécifié de nombres aléatoires sous forme de liste.

Nombre aléatoire (Normal) RanNorm#(,)

Utilise la distribution normale pour générer un nombre aléatoire de 10 chiffres en fonction de la moyenne $μ$ et de l’écart type $σ$ spécifiés.

Syntaxe : RanNorm#( $σ$ , $μ$ [, $n$ ]) $σ$ > 0, 1 ≤ $n$ ≤ 999

$n$ : Spécifie le nombre de nombres aléatoires. S’il est omis, un nombre aléatoire est renvoyé. Si spécifié, renvoie le nombre spécifié de nombres aléatoires sous forme de liste.

Exemple : Générer un nombre aléatoire de valeurs de taille obtenues selon une distribution normale pour un groupe d’enfants de moins d’un an dont la taille moyenne est de 68 cm. Supposons que l’écart-type soit de 8 : RanNorm#(8,68)

Nombre aléatoire (Binomial) RanBin#(,)

Utilise la distribution binomiale en fonction du nombre d’essais $n$ spécifié et de la valeur de la probabilité $p$ pour générer un nombre entier aléatoire.

Syntaxe : RanBin#( $n$ , $p$ [, $m$ ]) 1 ≤ $n$ ≤ 100000, 1 ≤ $m$ ≤ 999, 0 ≤ $p$ ≤ 1

$m$ : Spécifie le nombre de nombres aléatoires. S’il est omis, un nombre aléatoire est renvoyé. Si spécifié, renvoie le nombre spécifié de nombres aléatoires sous forme de liste.

Nb aléatoire dans liste (0 à 1) RanList#()

Chaque exécution renvoie, sous forme de liste, le nombre spécifié de nombres aléatoires (0 à 1, 10 chiffres).

Syntaxe : RanList#( $n$ [, $a$ ]) 1 ≤ $a$ ≤ 9, 1 ≤ $n$ ≤ 999 ( $a$ , $n$ = entiers)

$n$ : Spécifie le nombre d’essais. Ce paramètre indique le nombre de nombres aléatoires à générer.

$a$ : Identique à Ran#.

Exemple : (Immédiatement après l’exécution de Ran# 0) RanList#(3,1) = {0.701320948,0.9297706456,0.2939058016}

Échant aléatoire de liste RanSamp#(,)

Prélève aléatoirement des éléments dans une liste et renvoie le résultat sous forme de liste.

Syntaxe : RanSamp#(List, $n$ [, $m$ ])

Liste : Une liste de variables (List 1 à List 26 ou List Ans)^* ou une liste

Les variables de liste peuvent également être spécifiées à l’aide de sous-noms.

$n$ : Nombre d’essais (1 ≤ $n$ ≤ 999 quand $m$ = 0, 1 ≤ $n$ ≤ nombre d’éléments dans List lorsque $m$ = 1)

$m$ : Spécifie 0 ou 1 (0 en cas d’omission). Lorsque $m$ = 0, chaque élément peut être extrait plusieurs fois. Lorsque $m$ = 1, chaque élément ne peut être extrait qu’une seule fois.

Exemple : Extraire deux éléments aléatoires de {1,3,6,7} : RanSamp#({1,3,6,7},2,1)
Extraire cinq éléments aléatoires de {1,3,6,7} : RanSamp#({1,3,6,7},5)

Calcul numérique

PGCD GCD(,)

Obtient le plus grand commun diviseur de plusieurs nombres entiers.

Syntaxe : GCD( $n$ , $m$ )

PPCM LCM(,)

Obtient le plus petit commun multiple de plusieurs entiers.

Syntaxe : LCM( $n$ , $m$ )

Valeur absolue Abs()

Recherche la valeur absolue de l’argument $n$ .

Syntaxe : | $n$ | Abs( $n$ )

Partie entière Int()

Extrait la partie entière de l’argument $n$ .

Syntaxe : Int( $n$ )

Exemple : Int(-3.5) = -3

Partie fractionnaire Frac()

Extrait la partie fractionnaire de l’argument $n$ .

Syntaxe : Frac( $n$ )

Exemple : Frac(-3.5) = -0.5

Arrondir Rnd

Cette fonction est disponible dans l’onglet Calcul de l’application Calculs. Elle arrondit la valeur du dernier résultat de calcul (Ans) sur l’affichage des résultats en fonction du réglage S > [Affichage].

Syntaxe : Rnd (pas d’argument, valable uniquement pour le résultat du calcul précédent)

Exemple : Alors que [Affichage] > [Fix3: 0.123], pour diviser 10 par 3 et ensuite multiplier Ans par 3

Rnd non utilisé :

10*3E
/3E

Rnd utilisé :

10*3E
C > [Calcul numérique] > [Arrondir]E
/3E

Lorsque le réglage est [Affichage] > [Fix3: 0.123], 10÷3=3.333 est affiché, mais 15 chiffres sont conservés en interne, de sorte que Ans×3=10.000. Si le résultat de 10÷3 est arrondi à l’aide de Rnd comme indiqué, Ans×3=9.999.

Partie entière Intg()

Renvoie le plus grand entier qui ne dépasse pas l’argument $n$ .

Syntaxe : Intg( $n$ )

Exemple : Intg(-10.56) = -11

Arrondi interne RndFix()

Arrondit l’argument $n$ à la position suivant le nombre de décimales spécifié par $m$ (0 à 9).

Syntaxe : RndFix( $n$ [, $m$ ])

Si $m$ est omis, l’arrondi est effectué conformément au réglage S > [Affichage], comme avec la fonction Rnd.

Non autorisé dans cette syntaxe : $d / d x$ , $d^{2} / d x^{2}$ , $∫ d x$ , Σ, FMin, FMax, Solve, RndFix, logab

Exemple : RndFix(1.23456,3) = 1.235

Reste division MOD(,)

Cette fonction permet d’obtenir le reste d’une opération de division. Elle renvoie le reste lorsque $n$ est divisé par $m$ .

Syntaxe : MOD( $n$ , $m$ ) ( $n$ , $m$ = entiers)

Exemple : MOD(17,3) = 2

Exponentiation modulaire MOD_Exp(,,)

Cette fonction calcule un exposant modulaire. Elle renvoie le reste lorsque $n$ est multiplié par $p$ puissance puis divisé par $m$ .

Syntaxe : MOD_Exp( $n$ , $p$ , $m$ ) ( $n$ , $p$ , $m$ = entiers)

Exemple : MOD(2,4,3) = 1

Conversions d’unité

Convertit une valeur d’une unité en une autre unité.

Syntaxe : Commande d’unité $n$ Unit Conversions commande d’unité ( $n$ = nombre réel ou liste de nombres réels)

Les deux commandes d’unité sont liées avec « Unit Conversions » et utilisées comme une seule commande de conversion d’unité. Les deux commandes d’unité doivent appartenir à la même catégorie. Reportez-vous à la « Liste des commandes d’unité » ci-dessous pour connaître les commandes d’unité disponibles.

Exemple : 25.4 [cm] Unit Conversions [in] = 10 ; {175,162} [m²] [ha] = {0.0175,0.0162}

Liste des commandes d’unité

Catégorie	Commande d’unité
Longueur	[fm]
	[Å]
	[μm]
	[mm]
	[cm]
	[m]
	[km]
	[AU]
	[l.y.]
	[pc]
	[Mil]
	[in]
	[ft]
	[yd]
	[fath]
	[rd]
	[mile]
	[n mile]
Aire	[cm²]
	[m²]
	[ha]
	[km²]
	[in²]
	[ft²]
	[yd²]
	[acre]
	[mile²]
Volume	[cm³]
	[mL]
	[L]
	[m³]
	[in³]
	[ft³]
	[fl_oz(UK)]
	[fl_oz(US)]
	[gal(US)]
	[gal(UK)]
	[pt]
	[qt]
	[tsp]
	[tbsp]
	[cup]
Temps	[ns]
	[μs]
	[ms]
	[s]
	[min]
	[h]
	[day]
	[week]
	[yr]
	[s-yr]
	[t-yr]
Température	[°C]
	[K]
	[°F]
	[°R]
Vitesse	[m/s]
	[km/h]
	[knot]
	[ft/s]
	[mile/h]
Masse	[u]
	[mg]
	[g]
	[kg]
	[mton]
	[oz]
	[lb]
	[slug]
	[ton(short)]
	[ton(long)]
Force	[N]
	[lbf]
	[tonf]
	[dyne]
	[kgf]
Pression	[Pa]
	[kPa]
	[mmH₂O]
	[mmHg]
	[atm]
	[inH₂O]
	[inHg]
	[lbf/in²]
	[bar]
	[kgf/cm²]
Énergie	[eV]
	[J]
	[cal_th]
	[cal₁₅]
	[cal_IT]
	[kcal_th]
	[kcal₁₅]
	[kcal_IT]
	[l-atm]
	[kW･h]
	[ft･lbf]
	[Btu]
	[erg]
	[kgf･m]
Puissance	[W]
	[cal_th/s]
	[hp]
	[ft･lbf/s]
	[Btu/min]

Données variables

La catégorie Données variables contient des variables qui stockent les valeurs d’entrée et de sortie de chaque application. Les éléments de menu qui apparaissent lorsque vous sélectionnez C > [Données variables] sont des noms d’applications.

Données variables > Statistiques

Les variables de cette catégorie stockent les valeurs d’entrée et les résultats des calculs statistiques effectués et des graphiques dessinés à l’aide de l’application Stats.

Statistiques > X

Calcul statistique à une ou deux variables des valuers de données de $x$ :

Élément du menu	Variable
Effectif total	n
Moyenne $\bar{x}$	$\bar{x}$
Écart-type σx	σx
Écart-type échantillon sx	sx
Minimum minX	minX
Maximum maxX	maxX
Somme $Σ x$	$Σ x$
Somme des carrés $Σ x^{2}$	$Σ x^{2}$

Statistiques > Y

Calcul statistique de variables appariées des valeurs des données de $y$ :

Élément du menu	Variable
Moyenne $\bar{y}$	$\bar{y}$
Écart-type σy	σy
Écart-type échantillon sy	sy
Minimum minY	minY
Maximum maxY	maxY
Somme $Σ y$	$Σ y$
Somme des carrés $Σ y^{2}$	$Σ y^{2}$
Somme des produits $Σ xy$	$Σ xy$

Statistiques > Graphe

Valeurs de sortie du calcul statistique à une variable :

Élément du menu	Variable
1er quartile Q1	$Q_{1}$
Médiane Med	Med
3ème quartile Q3	$Q_{3}$
Mode	Mod

Valeurs d’information du modèle de régression :

Élément du menu	Variable
Coefficient régression a	a
Coefficient régression b	b
Coefficient régression c	c
Coefficient régression d	d
Coefficient régression e	e
Coefficient corrélation r	r
Coeff détermination $r^{2}$	$r^{2}$
Erreur quadratique MSe	MSe

Statistiques > PTS

Coordonnées des points récapitulatifs au moment de l’exécution de Régression Med-Med :

Élément du menu	Variable
Coordonnées point $x_{1}$	$x_{1}$
Coordonnées point $x_{2}$	$x_{2}$
Coordonnées point $x_{3}$	$x_{3}$
Coordonnées point $y_{1}$	$y_{1}$
Coordonnées point $y_{2}$	$y_{2}$
Coordonnées point $y_{3}$	$y_{3}$

Statistiques > Entrée

Valeurs de saisie des calculs statistiques :

Élément du menu	Variable
Effectif total n	n
Moyenne $\bar{x}$	$\bar{x}$
Écart-type échantillon sx	sx
Taille échantillon 1 n1	n1
Taille échantillon 2 n2	n2
Moyenne échantillon 1 $\bar{x}$ 1	$\bar{x}$ 1
Moyenne échantillon 1 $\bar{x}$ 2	$\bar{x}$ 2
Écart-type échantill 1 sx1	sx1
Écart-type échantill 2 sx2	sx2
Écart-type échantill p sp	sp

Statistiques > Résultat > Test

Résultats du calcul des tests :

Élément du menu	Variable
p	p
z	z
t	t
$χ^{2}$	$χ^{2}$
F	F
Proportion estimée $\hat{p}$	$\hat{p}$
Proportion estimée $\hat{p}$ 1	$\hat{p}$ 1
Proportion estimée $\hat{p}$ 2	$\hat{p}$ 2
Degré de liberté df	df
Erreur standard se	se
Coefficient corrélation r	r
Coeff détermination $r^{2}$	$r^{2}$
Valeur p du facteur A pa	pa
Valeur F du facteur A Fa	Fa
Degré de liberté A Adf	Adf
Somme des carrés SSa	SSa
Moyenne des carrés MSa	MSa
Valeur p du fact B pb	pb
Valeur F du fact B Fb	Fb
Degré de liberté B Bdf	Bdf
Somme des carrés SSb	SSb
Moyenne des carrés MSb	MSb
Valeur p facteur AB pab	pab
Valeur F facteur AB Fab	Fab
Dégré de liberté AB ABdf	ABdf
Somme des carrés SSab	SSab
Moyenne des carrés MSab	MSab
Erreur degré de liberté Edf	Edf
Somme carrés erreurs SSe	SSe
Erreur quadratique MSe	MSe

Statistiques > Résultat > INTR

Résultats du calcul de l’intervalle de confiance :

Élément du menu	Variable
Limite inf Intervalle Conf	Lower
Limite sup Intervalle Conf	Upper
Proportion estimée $\hat{p}$	$\hat{p}$
Proportion estimée $\hat{p}$ 1	$\hat{p}$ 1
Proportion estimée $\hat{p}$ 2	$\hat{p}$ 2
Degré de liberté df	df

Données variables > Probabilités

Les variables de cette catégorie stockent les résultats des calculs de distribution effectués à l’aide de l’application Probabilités.

Élément du menu	Variable
p	p
Inverse x	xInv
Inverse normale x1	x1InvN
Inverse normale x2	x2InvN
Limite inf Normale zlow	zLow
Limite sup Normale zUp	zUp
Limite inf Student t	tLow
Limite sup Student t	tUp

Données variables > Table

Élément du menu	Variable	Description
Tableau de valeurs	F Result	Affiche le contenu de l’onglet Table de l’application Graph&Table sous forme de matrice.

Données variables > Récurrence

Élément du menu	Variable	Description
Tableau de valeurs	R Result	Affiche le contenu de l’onglet Table de l’application Suites sous forme de matrice.

Données variables > Équation

Les variables de cette catégorie stockent les valeurs saisies et les résultats des calculs pour les équations d’ordre supérieur ou les équations simultanées résolues à l’aide de l’application Équations.

Élément du menu	Variable	Description
Coeff équation polynomiale	Ply Coef	Affiche les coefficients de saisie des équations d’ordre supérieur sous forme de matrice.
Solutions équation polynom	Ply Result	Affiche les résultats du calcul des équations d’ordre supérieur sous forme de matrice.
Coefficients du système	Sim Coef	Affiche les coefficients des équations simultanées saisies sous forme de matrice.
Solutions du système	Sim Result	Affiche les résultats du calcul des équations simultanées sous forme de matrice.

Vecteur

Vct $n$ et Vct $m$ peuvent être des vecteurs ou des variables vectorielles.

La saisie des vecteurs indiqués dans l’exemple (tels que $[\begin{matrix} 1 & 2 \end{matrix}]$ ) se fait à l’aide de T > [m×n]. Pour plus de détails, consultez Saisie d’un vecteur dans un calcul.

Remarque

Lors du calcul du produit scalaire, du produit vectoriel et de l’angle formé par deux vecteurs, les dimensions des deux vecteurs doivent être identiques.

Vecteur Vct

Entre « Vct ». Ensuite, spécifiez une variable vectorielle en saisissant une lettre de A à Z ou Ans.

Produit scalaire DotP(,)

Obtient le produit vectoriel de deux vecteurs.

Syntaxe : DotP(Vct $n$ ,Vct $m$ )

Exemple : DotP( $[\begin{matrix} 1 & 2 \end{matrix}]$ , $[\begin{matrix} 3 & 4 \end{matrix}]$ ) = 11

Produit vectoriel CrossP(,)

Obtient le produit vectoriel de deux vecteurs.

Syntaxe : CrossP(Vct $n$ ,Vct $m$ ) (Les dimensions de Vct $n$ et de Vct $m$ doivent être 1 × 2, 1 × 3, 2 × 1 ou 3 × 1.)

Exemple : CrossP( $[\begin{matrix} 1 & 2 \end{matrix}]$ , $[\begin{matrix} 3 & 4 \end{matrix}]$ ) = $[\begin{matrix} 0 & 0 & - 2 \end{matrix}]$

Angle 2 vecteurs Angle(,)

Permet d’obtenir l’angle entre deux vecteurs.

Syntaxe : Angle(Vct $n$ ,Vct $m$ )

Exemple : Quand S > [Angle] > [Degrés], Angle( $[\begin{matrix} 1 & 1 \end{matrix}]$ , $[\begin{matrix} - 1 & 1 \end{matrix}]$ ) = 90

Vecteur unitaire UnitV()

Calcule le vecteur unitaire du vecteur spécifié en argument.

Syntaxe : UnitV(Vct $n$ )

Exemple : UnitV( $[\begin{matrix} 5 & 5 \end{matrix}]$ ) = $[\begin{matrix} \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{matrix}]$

Norme de vecteur Norm()

Calcule la norme (magnitude) d’un vecteur ou d’une matrice spécifiée.

Syntaxe : Norm(Vct $n$ ) ; Norm(Mat $n$ ) (Mat $n$ = matrice ou variable matricielle)

Exemple : Norm( $[\begin{matrix} 1 & 3 \end{matrix}]$ ) = $\sqrt{10}$ ; Norm( $[\begin{matrix} 1 & 3 \\ 2 & 4 \end{matrix}]$ ) = $\sqrt{30}$

Matrice

Mat $n$ et Mat $m$ sont des matrices ou des variables matricielles.

La saisie des matrices présentées dans l’exemple (telles que $[\begin{matrix} 0 & - 1 \\ 1 & 0 \end{matrix}]$ ) se fait à l’aide de T > [m×n]. Pour plus de détails, consultez Saisie d’une matrice dans un calcul.

Remarque

Les déterminants et les matrices inverses sont sujets à des erreurs dues à l’oubli de chiffres.

Les opérations sous forme d’échelon de lignes et sous forme d’échelon de lignes réduit peuvent ne pas produire des résultats précis en raison de chiffres manquants.

Matrice Mat

Entre « Mat ». Ensuite, saisissez une lettre de A à Z ou Ans pour spécifier une variable matricielle.

Déterminant Det()

Obtient le déterminant de la matrice carrée spécifiée.

Syntaxe : Det(Mat $n$ )

Exemple : Det( $[\begin{matrix} 1 & 3 \\ 2 & 4 \end{matrix}]$ ) = -2

Matrice inverse ^-1

Obtient l’inverse de la matrice carrée spécifiée.

Syntaxe : Mat $n^{- 1}$

Exemple : ${[\begin{matrix} 0 & - 1 \\ 1 & 0 \end{matrix}]}^{- 1}$ = $[\begin{matrix} 0 & 1 \\ - 1 & 0 \end{matrix}]$

Précautions

La précision des calculs est affectée pour les matrices dont le déterminant est proche de zéro.

Transposée Trn()

Obtient la matrice transposée de la matrice spécifiée.

Syntaxe : Trn(Mat $n$ )

Exemple : Trn( $[\begin{matrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{matrix}]$ ) = $[\begin{matrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{matrix}]$

Remarque

La commande « Trn » peut également être utilisée avec un vecteur. Elle convertit un vecteur 1 ligne × $n$ colonnes en un vecteur $n$ lignes × 1 colonne, ou un vecteur $m$ lignes × 1 colonne en un vecteur 1 ligne × $m$ colonne.

Matrice identité Identity()

Crée une matrice d’identité avec le nombre de lignes et de colonnes spécifié.

Syntaxe : Identity( $n$ ) ( $n$ = entier)

Exemple : Identity(2) = $[\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}]$

Forme échelonnée Ref()

Cette commande utilise l’algorithme d’élimination de Gauss pour trouver la forme d’échelon de ligne d’une matrice.

Syntaxe : Ref(Mat $n$ )

Exemple : Ref( $[\begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{matrix}]$ ) = $[\begin{matrix} 1 & \frac{5}{4} & \frac{3}{2} \\ 0 & 1 & 2 \end{matrix}]$

Forme échelonnée réduite Rref()

Obtient la forme réduite de l’échelon de ligne de la matrice spécifiée.

Syntaxe : Rref(Mat $n$ )

Exemple : Rref( $[\begin{matrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{matrix}]$ ) = $[\begin{matrix} 1 & 0 & - 1 \\ 0 & 1 & 2 \end{matrix}]$

Concaténer matrices Augment(,)

Combine deux matrices (ou vecteurs), chacune contenant le même nombre de lignes, en une seule matrice.

Syntaxe : Augment(Mat $m$ ,Mat $n$ ) ; Augment(Vct $m$ ,Vct $n$ )

L’une ou l’autre ou les deux matrices (Mat $m$ , Mat $n$ ) peut être remplacée par Vct $m$ , Vct $n$ , respectivement.

Exemple : Augment( $[\begin{matrix} 1 & 3 \\ 2 & 4 \end{matrix}]$ , $[\begin{matrix} 2 & 6 \\ 4 & 8 \end{matrix}]$ ) = $[\begin{matrix} 1 & 3 & 2 & 6 \\ 2 & 4 & 4 & 8 \end{matrix}]$ ; Augment( $[\begin{matrix} 1 \\ 2 \end{matrix}]$ , $[\begin{matrix} 2 & 6 \\ 4 & 8 \end{matrix}]$ ) = $[\begin{matrix} 1 & 2 & 6 \\ 2 & 4 & 8 \end{matrix}]$

Remplir la matrice Fill(,)

Remplace tous les éléments d’une variable matricielle (ou d’une variable vectorielle) par la valeur spécifiée $m$ .

Syntaxe : Fill( $m$ ,Mat $n$ ) ; Fill( $m$ ,Vct $n$ )

Dimensions Dim()

Obtient les dimensions d’une matrice (ou d’un vecteur) et les restitue sous forme de liste.

Syntaxe 1 : Dim(Mat $n$ ) ; Dim(Vct $n$ )

Le résultat de la commande Dim étant une liste, il est stocké dans List Ans.

Spécifie les dimensions sous forme de liste et crée une matrice (ou un vecteur) dont tous les éléments sont zéro.

Syntaxe 2 : { $a$ , $b$ } → Dim(Mat $n$ ) ( $a$ , $b$ = entiers, 1 ≤ $a$ ≤ 999, 1 ≤ $b$ ≤ 999) ;

{ $a$ , $b$ } → Dim(Vct $n$ ) ( $a$ , $b$ = entiers, 1 ≤ $b$ ≤ 999 quand $a$ = 1, 1 ≤ $a$ ≤ 999 quand $b$ = 1)

Nombre complexe

La lettre $z$ dans la syntaxe ci-dessous représente un nombre complexe. Les calculs qui utilisent Arg, Ir∠θ et Ia+b $i$ sont affectés par le réglage S > [Angle].

Remarque

La calculatrice considère un nombre complexe sous la forme a+b $i$ comme une coordonnée sur un plan de Gauss, et calcule la valeur absolue | $z$ | et l’argument Arg( $z$ ).

Module Abs()

Obtient la valeur absolue d’un nombre complexe.

Syntaxe : | $z$ | Abs( $z$ )

Exemple : |1+ $i$ | = $\sqrt{2}$

$i$ $i$

Saisissez l’unité imaginaire $i$ .

Ir∠θ Ir∠θ

Convertit une valeur de forme rectangulaire en forme polaire.

Syntaxe : $z$ Ir∠θ

Exemple : $1 + \sqrt{3} i$ Ir∠θ = 2∠60 (S > [Angle] > [Degrés])

Ia+b $i$ Ia+b $i$

Convertit une forme polaire en forme rectangulaire.

Syntaxe : $z$ Ia+b $i$

Exemple : 2∠60Ia+b $i$ = $1 + \sqrt{3} i$ (S > [Angle] > [Degrés])

Argument Arg()

Obtient l’argument d’un nombre complexe.

Syntaxe : Arg( $z$ )

Exemple : Arg(1+ $i$ ) = 45 (S > [Angle] > [Degrés])

Conjugué Conjg()

Obtient le nombre complexe conjugué.

Syntaxe : Conjg( $z$ )

Exemple : Conjg(1+ $i$ ) = 1 $- i$

Extr part réelle ReP()

Extrait la partie réelle d’un nombre complexe.

Syntaxe : ReP( $z$ )

Exemple : ReP(1+2 $i$ ) = 1

Partie imaginaire ImP()

Extrait la partie imaginaire d’un nombre complexe.

Syntaxe : ImP( $z$ )

Exemple : ImP(1+2 $i$ ) = 2

Statistiques

Dans toutes les syntaxes ci-dessous, « List $n$ » et « List $m$ » sont des listes ou des variables de liste. Pour les variables de liste, $n$ , $m$ peut être une valeur de 1 à 26, ou Ans. Les variables de liste peuvent également être spécifiées à l’aide de sous-noms.

{} {}

Entre des accolades ( { } ) pour saisir une nouvelle liste.

Liste List

Entre « List ». Après « List », saisissez une valeur comprise entre 1 et 26, ou Ans pour spécifier une variable de liste.

Minimum Min()

Syntaxe 1 : Min(List $n$ ) Extrait la valeur minimale de tous les éléments d’une liste.

Syntaxe 2 : Min(List $n$ ,List $m$ ) Extrait l’élément le plus petit à la même position dans deux listes.

Maximum Max()

Syntaxe 1 : Max(List $n$ ) Extrait la valeur maximale de tous les éléments d’une liste.

Syntaxe 2 : Max(List $n$ ,List $m$ ) Extrait l’élément le plus grand à la même position dans deux listes.

Moyenne Mean()

Permet de trouver la valeur moyenne de tous les éléments d’une liste.

Syntaxe : Mean(List $n$ )

Médiane Median()

Permet de trouver la médiane de deux listes, dont l’une est constituée de données et l’autre de fréquences.

Syntaxe : Median(List $n$ ,List $m$ )

List $n$ : liste de données, List $m$ : liste de fréquence
Le nombre d’éléments dans List $n$ et List $m$ doit être identique.

Exemple : Lorsque List 1 = {36,16,58,46,56}, List 2 = {75,89,98,72,67}, Median(List 1,List 2) = 46

Écart-type StdDev() StdDev()

Permet de trouver l’écart-type de l’échantillon de données spécifiées par une liste.

Syntaxe : StdDev(List $n$ [,List $m$ ]) (List $n$ ... Exemple de données, List $m$ ... Données de fréquence)

Exemple : StdDev({10,20,30,40},{3,5,4,1}) = 9.26808696

Écart-type StdDev_σ() StdDev_σ()

Permet de trouver l’écart-type de la population pour des données spécifiées par une liste.

Syntaxe : StdDev_σ(List $n$ [,List $m$ ]) (List $n$ ... Exemple de données, List $m$ ... Données de fréquence)

Variance échantillon Variance() Variance()

Permet de trouver la variance sans biais des données spécifiées par une liste.

Syntaxe : Variance(List $n$ [,List $m$ ]) (List $n$ ... Exemple de données, List $m$ ... Données de fréquence)

Variance Variance_ $σ^{2}$ () Variance_ $σ^{2}$ ()

Permet de trouver la variance de la population des données spécifiées par une liste.

Syntaxe : Variance_ $σ^{2}$ (List $n$ [,List $m$ ]) (List $n$ ... Exemple de données, List $m$ ... Données de fréquence)

Remplir la liste Fill(,)

Remplace les valeurs de tous les éléments d’une variable de liste par la même valeur ( $a$ ).

Syntaxe : Fill( $a$ ,List $n$ )

Générer une suite Seq(,,,,)

Définit une fonction qui génère une séquence de nombres et la renvoie sous forme de liste.

Syntaxe : Seq( $f (x)$ , $x$ ,Valeur de départ,Valeur de fin,Incrément)

$x$ peut être n’importe quelle variable alphabétique.

Exemple : Seq( $x^{2}$ , $x$ ,1,11,5) = {1,36,121}

Fréquence cumulée Cuml()

Calcule la fréquence cumulée des éléments d’une liste.

Syntaxe : Cuml(List $n$ )

Exemple : Quand List 1 = {2,3,6,5,4}, Cuml(List 1) = {2,5,11,16,20}

Pourcent données Percent()

Calcule le pourcentage de chaque élément par rapport à la somme de tous les éléments d’une liste.

Syntaxe : Percent(List $n$ )

Liste différences Δlist ΔList

Calcule {Élément 2 - Élément 1, Élément 3 - Élément 2, ... Element $n$ - Élément $n$ -1} dans une liste de $n$ ( $n$ ≥ 2) éléments et renvoie le résultat sous forme de liste.

Syntaxe : ΔList $a$ ( $a$ = Numéro de variable de liste)

Remarque : vous pouvez enregistrer le résultat dans la liste 2 en appuyant sur « ΔList 1→List 2 ».

Concaténer listes Augment(,)

Combine deux listes en une seule.

Syntaxe : Augment(List $n$ ,List $m$ )

Somme éléments de la liste Sum()

Permet de trouver la somme de tous les éléments d’une liste.

Syntaxe : Sum(List $n$ )

Produit ds liste Prod()

Permet de trouver le produit de la somme de tous les éléments d’une liste.

Syntaxe : Prod(List $n$ )

Valeur estimée x $\hat{x}$
Valeur estimée y $\hat{y}$

Ces fonctions sont utilisées immédiatement après avoir effectué un calcul de régression^* avec l’application Stats. Pour une valeur spécifiée pour une variable ( $x$ ou $y$ ), estime l’autre variable, sur la base d’un modèle de régression.

Syntaxe : Valeur de $y$ $\hat{x}$ (Calcule une valeur estimée de $x$ pour la valeur de $y$ .)

Valeur de $x$ $\hat{y}$ (Calcule la valeur estimée de $y$ pour la valeur de $x$ .)

Les valeurs estimées ne peuvent pas être calculées pour les types de graphiques de régression suivants : Régression Med-Med, Régression a $x^{2}$ +b $x$ +c, Régression a $x^{3}$ +b $x^{2}$ +c $x$ +d, Régression a $x^{4}$ +b $x^{3}$ +c $x^{2}$ +…, Régression sinusoïdale, Régression a+b･ln( $x$ ).

Liste vers matrice List→Mat()

Enregistre le contenu de la liste dans Mat Ans.

Syntaxe : List→Mat(List $n$ ,List $m$ )
(Le nombre d’éléments dans List $n$ et List $m$ doit être identique.)

Exemple : Quand List 1 = {2,3,4}, List 2 = {20,30,40}, List→Mat(List 1,List 2) = $[\begin{matrix} 2 & 20 \\ 3 & 30 \\ 4 & 40 \end{matrix}]$

Matrice vers liste Mat→List()

Enregistre les colonnes spécifiées d’une variable matricielle dans List Ans.

Syntaxe : Mat→List(Mat $n$ , $m$ )
( $n$ est une lettre de A à Z, ou Ans, et $m$ est un numéro de colonne.)

Exemple : Quand Mat A = $[\begin{matrix} 2 & 20 \\ 3 & 30 \\ 4 & 40 \end{matrix}]$ , Mat→List(Mat A,1) = {2,3,4}

Remarque : Vous pouvez attribuer les éléments de la colonne 1 du tableau A à la liste 1 en saisissant « Mat→List(Mat A,1)→List 1 ».

Dimensions Dim()

Détermine le nombre d’éléments d’une liste.

Syntaxe 1 : Dim(List $n$ )

Spécifie le nombre d’éléments de la liste et crée une variable de liste avec zéro dans tous les éléments.

Syntaxe 2 : Nombre d’éléments $a$ → Dim(List $n$ ) ( $a$ = entier, 1 ≤ $a$ ≤ 999)

Angle/Coord/Sexa

Degrés °

Spécifie les degrés comme unité d’angle.

Syntaxe : $n$ °

Exemple : Quand S > [Angle] > [Radians], 90° = $\frac{1}{2} π$

Radians $^{r}$

Spécifie les radians comme unité angulaire.

Syntaxe : $n^{r}$

Exemple : Quand S > [Angle] > [Degrés], $\frac{π}{2}^{r}$ = 90

Grades $^{g}$

Spécifie les gradians comme unité d’angle.

Syntaxe : $n^{g}$

Exemple : Quand S > [Angle] > [Degrés], $100^{g}$ = 90

Décimal en sexagésimal IDMS

Convertit une valeur décimale en valeur sexagésimale (degrés (heures), minutes, secondes).

Syntaxe : $n$ IDMS

Exemple : 1.25IDMS = 1°15’00”

Coordonnées polaires Pol(,)

Convertit les valeurs de coordonnées rectangulaires en coordonnées polaires et les renvoie sous forme de liste.

Syntaxe : Pol( $x$ , $y$ ) = ( $r$ , $θ$ )

Les coordonnées polaires résultantes $θ$ sont affichés dans la plage de -180° < $θ$ ≤ 180°. Il en va de même pour les radians et les gradians.

Exemple : Quand S > [Angle] > [Degrés], Pol( $\sqrt{2}$ , $\sqrt{2}$ ) = {2,45}

Coordonnées cartésiennes Rec(,)

Convertit les valeurs des coordonnées polaires en coordonnées rectangulaires et les renvoie sous forme de liste.

Syntaxe : Rec( $r$ , $θ$ ) = ( $x$ , $y$ )

Exemple : Quand S > [Angle] > [Degrés], Rec(2,45) = { $\sqrt{2}$ , $\sqrt{2}$ }

Deg Min Sec °

Entre une valeur sexagésimale.

Syntaxe : Valeur en degrés°[Valeur en minutes°[Valeur en secondes]]

Exemple : 1°15° = 1.25 ; 0°75° = 1.25 ; 0°15° = 0.25 ; 0°0°900° = 0.25

Remarque : Pour afficher les résultats des calculs sous forme de valeurs sexagésimales, sélectionnez F > [Sexagésimal]. Pour plus d’informations, consultez Modification du format d’affichage des résultats de calcul (menu Format).

Lois de probabilités : Calcul des probabilités pour une distribution normale standard

Chaque fonction mathématique décrite dans cette section est destinée à être utilisée immédiatement après avoir effectué un calcul statistique Stats à 1 variable avec l’application Stats.

Normale(0,1) P(t)=P(X≤t)     P()
Normale(0,1) Q(t)=P(0≤X≤t)     Q()
Normale(0,1) R(t)=P(X≥t)     R()

En prenant la variable normalisée $t$ comme argument, ces fonctions trouvent les valeurs de probabilité pour la distribution normale standard illustrée dans les figures ci-dessous. La valeur de $t$ est déterminée à l’aide de la fonction t().

Syntaxe : P( $t$ ) ; Q( $t$ ) ; R( $t$ )

Centrée-réd t(x)=(x-x̄)/σx t()

La variable normalisée t( $x$ ) à la valeur de données $x$ est déterminée à l’aide de la formule ci-dessous sur la base de la moyenne $\bar{x}$ et de l’écart-type de la population $σ_{x}$ , qui est obtenu comme le résultat du calcul statistique Stats à 1 variable.

$t (x) = \frac{x - \bar{x}}{σ_{x}}$

Syntaxe : t( $x$ )

Cette fonction est utilisée en combinaison avec P(, Q( et R( pour trouver les valeurs de probabilité de la distribution normale standard.

Exemple : Les données de taille de 20 élèves d’une université ont été saisies avec l’application Stats et un calcul statistique Stats à 1 variable a été effectué. Déterminez dans quel percentile se situe l’élève mesurant 180 cm.

R(t(180))

Lois de probabilités : Calculs de distribution

Chaque fonction de cette section effectue un type différent de calcul de distribution.

Remarques sur la syntaxe

La liste ci-dessous indique la signification des symboles et des abréviations dans la syntaxe.

$x$ : valeur des données

Lower : limite inférieure

Upper : limite supérieure

$μ$ : moyenne de la population

$σ$ : écart-type de la population ( $σ$ > 0)

$λ$ : moyenne ( $λ$ > 0)

$p$ : probabilité (0 ≤ $p$ ≤ 1)

df : degrés de liberté (df > 0)

$n$ :df : degrés de liberté du numérateur (nombre entier positif)

$d$ :df : degrés de liberté du dénominateur (nombre entier positif)

$P$ : probabilité de réussite (0 ≤ $P$ ≤ 1)

$n$ : nombre d’essais de la population (0 ≤ $n$ entier)

$M$ : nombre de succès dans la population (0 ≤ $M$ entier)

$N$ : taille de la population ( $n$ ≤ $N$ , $M$ ≤ $N$ entier)

Les valeurs suivantes sont substituées lorsque l’un des arguments entre crochets ([ ]) est omis.
$μ$ =0, $σ$ =1, queue=”L” (gauche)

Résultat du calcul Variables de stockage

Les variables (p, xInv, x1InvN, x2InvN, zLow, zUp, tLow, tUp) dans lesquelles sont stockés les résultats des calculs de chaque fonction sont accessibles à partir de C > [Données variables] > [Probabilités].

Densité normale (x,σ,μ) NormPD()

Renvoie la densité de probabilité normale (valeur de $p$ ) pour les données spécifiées.

Syntaxe : NormPD( $x$ [, $μ$ , $σ$ ])

Une valeur unique ou une liste peut être spécifiée pour $x$ . Le résultat du calcul de $p$ est attribué aux variables $p$ et Ans (List Ans quand $x$ est une liste).

Exemple : NormPD(1) = 0.2419707245 ; NormPD({0.5,1}) = {0.3520653268,0.2419707245}

Normale P(a≤X≤b) (a,b,σ,μ) NormCD(,)

Renvoie la distribution cumulative normale (valeur de $p$ ) pour les données spécifiées.

Syntaxe : NormCD(Lower,Upper[, $μ$ , $σ$ ])

Des valeurs individuelles ou des listes peuvent être spécifiées pour Lower et Upper. Les résultats de calcul de $p$ , zLow et zUp sont attribués respectivement aux variables $p$ , zLow et zUp. Le résultat du calcul de $p$ est également attribué à Ans (List Ans lorsque Lower et Upper sont des listes).

Exemple : NormCD(-1,1) = 0.6826894921 ; NormCD({-1,-2},{1,2}) = {0.6826894921,0.9544997361}

Inverse Normale (p,σ,μ) InvNormCD()

Renvoie la distribution cumulative normale inverse (valeur(s) inférieure(s) et/ou supérieure(s)) pour la valeur de $p$ spécifiée.

Syntaxe : InvNormCD([queue,] $p$ [, $μ$ , $σ$ ])

Vous pouvez spécifier Left, Right ou Center pour la « queue ». Pour spécifier le réglage de la « queue », saisissez les chiffres ou les lettres ci-dessous.

Left : -1 ou ”L”

Center : 0 ou ”C”

Right : 1 ou ”R”

Une valeur unique ou une liste peut être spécifiée pour $p$ . Les résultats des calculs sont édités en fonction du réglage de la queue, comme décrit ci-dessous.

queue = Left	La valeur Upper est attribuée aux variables x1InvN et Ans (Liste Ans quand $p$ est une liste).
queue = Right	La valeur Lower est attribuée aux variables x1InvN et Ans (Liste Ans quand $p$ est une liste).
queue = Central	Les valeurs Lower et Upper sont attribuées respectivement aux variables x1InvN et x2InvN. Seule la valeur Lower est attribuée à Ans (List Ans quand $p$ est une liste).

Exemple : InvNormCD(”L”,0.7,35,2) = 36.04880103
InvNormCD({0.5,0.7},35,2) = {35,36.04880103}

Densité Student t (x,df) tPD(,)

Renvoie la densité de probabilité de Student- $t$ (valeur de $p$ ) pour les données spécifiées.

Syntaxe : tPD( $x$ ,df)

Consultez Syntaxe PD.

Exemple : tPD(1,1) = 0.1591549431 ; tPD({0,1},1) = {0.3183098862,0.1591549431}

Student P(a≤X≤b) (a,b,df) tCD(,,)

Renvoie la distribution cumulative de Student- $t$ (valeur de $p$ ) pour les données spécifiées.

Syntaxe : tCD(Lower,Upper,df)

Des valeurs individuelles ou des listes peuvent être spécifiées pour Lower et Upper. Les résultats de calcul de $p$ , tLow et tUp sont attribués respectivement aux variables $p$ , tLow et tUp. Le résultat du calcul de $p$ est également attribué à Ans (List Ans lorsque Lower et Upper sont des listes).

Exemple : tCD(0,1,1) = 0.25 ; tCD({0,0},{1,2},1) = {0.25,0.3524163823}

Inverse Student (p,df) InvTCD(,)

Renvoie la distribution cumulative inverse de Student- $t$ (valeur Lower) de la valeur de $p$ spécifiée.

Syntaxe : InvTCD( $p$ ,df)

Consultez Syntaxe CD inverse (distributions continues).

Exemple : InvTCD(0.25,1) = 1 ; InvTCD({0.25,0.75},1) = {1,-1}

Densité $χ^{2}$ (x,df) ChiPD(,)

Renvoie la densité de probabilité $χ^{2}$ (valeur de $p$ ) pour les données spécifiées.

Syntaxe : ChiPD( $x$ ,df)

Consultez Syntaxe PD.

Exemple : ChiPD(1,1) = 0.2419707245 ; ChiPD({0,1},1) = {0,0.2419707245}

$χ^{2}$ P(a≤X≤b) (a,b,df) ChiCD(,,)

Renvoie la distribution cumulative $χ^{2}$ (valeur de $p$ ) pour les données spécifiées.

Syntaxe : ChiCD(Lower,Upper,df)

Consultez Syntaxe CD.

Exemple : ChiCD(0,1,1) = 0.6826894921 ; ChiCD({0,0},{1,2},1) = {0.6826894921,0.8427007929}

Inverse $χ^{2}$ (p,df) InvChiCD(,)

Renvoie la distribution cumulative inverse $χ^{2}$ (valeur Lower) de la valeur de $p$ spécifiée.

Syntaxe : InvChiCD( $p$ ,df)

Consultez Syntaxe CD inverse (distributions continues).

Exemple : InvChiCD(0.319,1) = 0.9930420738 ; InvChiCD({0.64,0.319},1) = {0.2187421667,0.9930420738}

Densité Fisher(x,ndf,ddf) FPD(,,)

Renvoie la densité de probabilité $F$ (valeur de $p$ ) pour les données spécifiées.

Syntaxe : FPD( $x$ , $n$ :df, $d$ :df)

Consultez Syntaxe PD.

Exemple : FPD(1,1,2) = 0.1924500897 ; FPD({1,2},1,2) = {0.1924500897,0.08838834765}

Fisher a≤X≤b (a,b,ndf,ddf) FCD(,,,)

Renvoie la distribution cumulative $F$ (valeur de $p$ ) pour les données spécifiées.

Syntaxe : FCD(Lower,Upper, $n$ :df, $d$ :df)

Consultez Syntaxe CD.

Exemple : FCD(0,1,1,2) = 0.5773502692 ; FCD({0,0},{1,2},1,2) = {0.5773502692,0.7071067812}

Inverse Fisher (p,ndf,ddf) InvFCD(,,)

Renvoie la distribution cumulative inverse $F$ (valeur Lower) de la valeur de $p$ spécifiée.

Syntaxe : InvFCD( $p$ , $n$ :df, $d$ :df)

Consultez Syntaxe CD inverse (distributions continues).

Exemple : InvFCD(0.43,1,2) = 0.9625240705 ; InvFCD({0.86,0.43},1,2) = {0.03998368013,0.9625240705}

Binomiale P(x=k) (k,n,p) BinomialPD(,)

Renvoie la probabilité binomiale (valeur de $p$ ) pour les données spécifiées.

Syntaxe : BinomialPD([ $x$ ,] $n$ , $P$ )

Consultez Syntaxe PD.

Exemple : BinomialPD(3,5,0.5) = 0.3125 ; BinomialPD({3,5},5,0.5) = {0.3125,0.03125}

Binomiale a≤X≤b (a,b,n,p) BinomialCD(,)

Renvoie la distribution cumulative binomiale (valeur de $p$ ) pour les données spécifiées.

Syntaxe : BinomialCD([[Lower,]Upper,] $n$ , $P$ )

Consultez Syntaxe CD.

Exemple : BinomialCD(5,10,0.5) = 0.623046875 ; BinomialCD({0,5},{5,8},10,0.5) = {0.623046875,0.6123046875}

Inverse Binomiale (p,n,P) InvBinomialCD(,,)

Renvoie la distribution cumulative binomiale inverse de la valeur de $p$ spécifiée.

Syntaxe : InvBinomialCD( $p$ , $n$ , $P$ )

Consultez Syntaxe CD inverse (distributions discrètes).

Exemple : InvBinomialCD(0.6,10,0.5) = 5 ; InvBinomialCD({0.6,0.3},10,0.5) = {5,4}

Précautions

Lors de l’exécution du calcul de la distribution cumulative binomiale inverse, la calculatrice utilise la valeur de $p$ spécifiée et la valeur inférieure d’un chiffre au nombre minimum de chiffres significatifs de la valeur $p$ (valeur de $p$ ’) pour calculer les valeurs du nombre minimum d’essais. Les résultats sont attribués aux variables xInv (résultat du calcul utilisant $p$ ) et *xInv (résultat du calcul utilisant $p$ ’). La calculatrice n’affiche toujours que la valeur xInv. Toutefois, lorsque les valeurs xInv et *xInv sont différentes, le message ci-dessous s’affiche avec les deux valeurs.

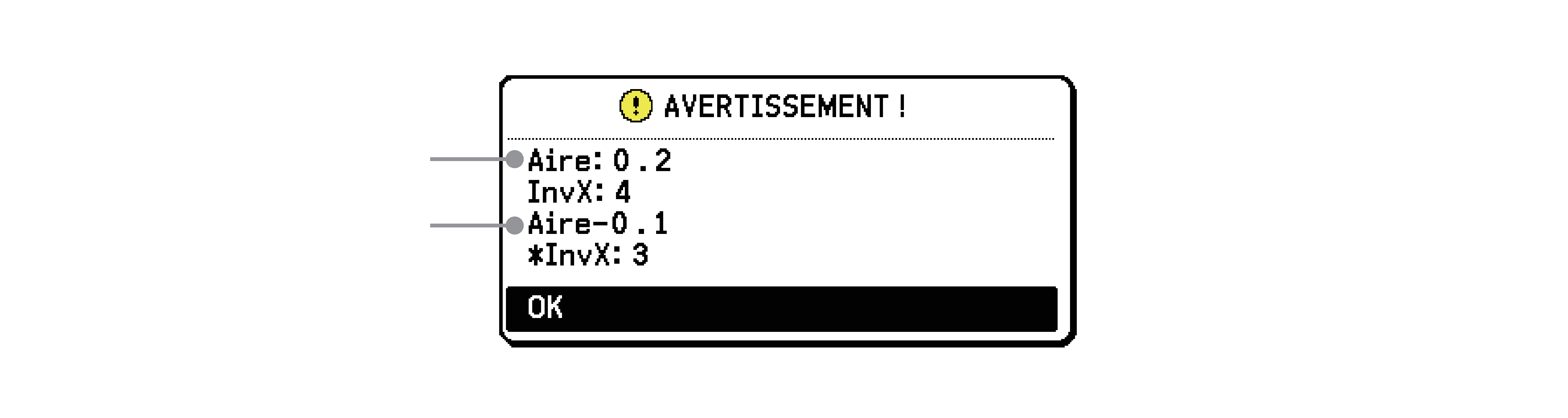
CY875_Catalog Distribution_2 + CY875_Catalog Distribution_2

Valeur de $p$

Valeur de $p$ ’

Les résultats du calcul de la distribution cumulative binomiale inverse sont des nombres entiers. La précision peut être réduite lorsque la valeur de $p$ comporte 10 chiffres ou plus. Veuillez noter que même une légère différence dans la précision des calculs affecte les résultats des calculs. Si un message d’avertissement s’affiche, vérifiez les valeurs affichées.

Poisson P(x=k) (k,λ) PoissonPD(,)

Renvoie la probabilité de Poisson (valeur de $p$ ) pour les données spécifiées.

Syntaxe : PoissonPD( $x$ , $λ$ )

Consultez Syntaxe PD.

Exemple : PoissonPD(1,1.2) = 0.3614330543 ; PoissonPD({1,2},1.2) = {0.3614330543,0.2168598326}

Poisson P(a≤X≤b) (a,b,λ) PoissonCD(,)

Renvoie la distribution cumulative de Poisson (valeur de $p$ ) pour les données spécifiées.

Syntaxe : PoissonCD([Lower,]Upper, $λ$ )

Consultez Syntaxe CD.

Si Lower est omise, on suppose que Lower = 0.

Exemple : PoissonCD(1,2,1.2) = 0.5782928869 ; PoissonCD({1,1},{2,3},1.2) = {0.5782928869,0.6650368199}

Inverse Poisson (p,λ) InvPoissonCD(,)

Renvoie la distribution cumulative inverse de Poisson de la valeur de $p$ spécifiée.

Syntaxe : InvPoissonCD( $p$ , $λ$ )

Consultez Syntaxe CD inverse (distributions discrètes).

Exemple : InvPoissonCD(0.58,1.2) = 1 ; InvPoissonCD({0.58,0.75},1.2) = {1,2}

Les précautions sont les mêmes que pour Inverse Binomiale (p,n,P).

Géométrique P(x=k) (k,p) GeoPD(,)

Renvoie la probabilité géométrique (valeur de $p$ ) pour les données spécifiées.

Syntaxe : GeoPD( $x$ , $P$ )

Consultez Syntaxe PD.

Exemple : GeoPD(2,0.8) = 0.16 ; GeoPD({2,3},0.8) = {0.16,0.032}

Géométrique a≤X≤b (a,b,p) GeoCD(,)

Renvoie la distribution géométrique cumulative (valeur de $p$ ) pour les données spécifiées.

Syntaxe : GeoCD([Lower,]Upper, $P$ )

Consultez Syntaxe CD.

Si Lower est omise, on suppose que Lower = 0.

Exemple : GeoCD(1,2,0.8) = 0.96 ; GeoCD({1,1},{2,3},0.8) = {0.96,0.992}

Inverse Géométrique (p,P) InvGeoCD(,)

Renvoie la distribution géométrique cumulative inverse de la valeur de $p$ spécifiée.

Syntaxe : InvGeoCD( $p$ , $P$ )

Consultez Syntaxe CD inverse (distributions discrètes).

Exemple : InvGeoCD(0.96,0.8) = 2 ; InvGeoCD({0.96,0.992},0.8) = {2,3}

Les précautions sont les mêmes que pour Inverse Binomiale (p,n,P).

Hypergéo P(x=k) (k,n,M,N) HypergeoPD(,,,)

Renvoie la probabilité hypergéométrique (valeur de $p$ ) pour les données spécifiées.

Syntaxe : HypergeoPD( $x$ , $n$ , $M$ , $N$ )

Consultez Syntaxe PD.

Exemple : HypergeoPD(1,5,10,20) = 0.1354489164 ; HypergeoPD({1,2},5,10,20) = {0.1354489164,0.3482972136}

Hypergéo a≤X≤b (a,b,n,M,N) HypergeoCD(,,,)

Renvoie la distribution hypergéométrique cumulative (valeur de $p$ ) pour les données spécifiées.

Syntaxe : HypergeoCD([Lower,]Upper, $n$ , $M$ , $N$ )

Consultez Syntaxe CD.

Si Lower est omise, on suppose que Lower = 0.

Exemple : HypergeoCD(1,2,5,10,20) = 0.48374613 ; HypergeoCD({1,1},{2,3},5,10,20) = {0.48374613,0.8320433437}

Inverse Hypergéo (p,n,M,N) InvHypergeoCD(,,,)

Renvoie la distribution hypergéométrique cumulative inverse de la valeur de $p$ spécifiée.

Syntaxe : InvHypergeoCD( $p$ , $n$ , $M$ , $N$ )

Consultez Syntaxe CD inverse (distributions discrètes).

Exemple : InvHypergeoCD(0.48,5,10,20) = 2 ; InvHypergeoCD({0.48,0.83},5,10,20) = {2,3}

Les précautions sont les mêmes que pour Inverse Binomiale (p,n,P).

Syntaxe et description

Syntaxe	Description
Syntaxe PD	Une valeur unique ou une liste peut être spécifiée pour $x$ . Le résultat du calcul de $p$ est attribué aux variables $p$ et Ans (List Ans quand $x$ est une liste).
Syntaxe CD	Des valeurs individuelles ou des listes peuvent être spécifiées pour Lower et Upper. Le résultat du calcul de $p$ est attribué aux variables $p$ et Ans (List Ans lorsque Lower et Upper sont des listes).
Syntaxe CD inverse (distributions continues)	Une valeur unique ou une liste peut être spécifiée pour $p$ . La valeur de Lower est attribuée aux variables xInv et Ans (List Ans quand $p$ est une liste).
Syntaxe CD inverse (distributions discrètes)	Une valeur unique ou une liste peut être spécifiée pour $p$ . La valeur X du résultat du calcul est attribuée aux variables xInv et Ans (List Ans quand $p$ est une liste).

Fonction hyperbolique

Les fonctions hyperboliques et hyperboliques inverses peuvent être saisies à l’aide des éléments de menu ci-dessous.

Élément du menu	Fonction
sinh	sinh()
cosh	cosh()
tanh	tanh()
sinh $^{-1}$	sinh $^{-1}$ ()
cosh $^{-1}$	cosh $^{-1}$ ()
tanh $^{-1}$	tanh $^{-1}$ ()

Exemple : sinh(1) = 1.175201194 ; sinh $^{-1}$ (Ans) = 1

Préfixes d’unité

Les symboles d’ingénierie peuvent être saisis à l’aide des éléments de menu ci-dessous.

Élément du menu	Symbole	$10^{n}$
Milli	m	$10^{-3}$
Micro	μ	$10^{-6}$
Nano	n	$10^{-9}$
Pico	p	$10^{-12}$
Femto	f	$10^{-15}$
Kilo	k	$10^{3}$
Méga	M	$10^{6}$
Giga	G	$10^{9}$
Téra	T	$10^{12}$
Péta	P	$10^{15}$
Exa	E	$10^{18}$

L’ajout d’un symbole d’ingénierie immédiatement après une valeur fait que la valeur est $10^{n}$ (où $n$ est un multiple entier de 3).

Exemple : 7.1k = 7100 ; 2G÷100M = 20

Remarque : Pour afficher les résultats des calculs avec des symboles d’ingénierie, activez l’option S > [Affichage] > [Symbole ingénieur]. Pour plus de détails, consultez Affichage (général).

Symboles

Ce menu comprend les symboles figurant dans le tableau ci-dessous.

＾	<	(	}
:	>	)
=	≤	[	-
”	≥	]	∠
,	≠	{	~

Tout > A to Z

C > [Tout] affiche une liste alphabétique de toutes les fonctions, commandes et variables d’application de la calculatrice. Pour plus de détails, consultez Détails du menu Catalogue.

Tout > Symboles

Ce menu comprend les fonctions et les symboles figurant dans le tableau ci-dessous.

$\sqrt[3]{}$ ()	$π$		E (Préfixes d’unité)
$_{10}$ ^()	!	-	P (Préfixes d’unité)
{	° (Degrés)	∠	T (Préfixes d’unité)
}	$^{r}$ (Radians)	:	G (Préfixes d’unité)
≠	$^{g}$ (Grades)		M (Préfixes d’unité)
<	°	=	k (Préfixes d’unité)
>	$\sqrt{}$ ()	,	m (Préfixes d’unité)
≤	$\sqrt[x]{}$	(	$μ$ (Préfixes d’unité)
≥	$^{-1}$	)	n (Préfixes d’unité)
”	$^{2}$	[	p (Préfixes d’unité)
~	＾	]	f (Préfixes d’unité)

Détails du menu Catalogue

Utiliser l’historique des saisies

Épinglage de l’historique des saisies

Liste des éléments regroupés par catégorie

Étude de fonction

Dérivée (d/dx) d/dx(,)

Dérivée 2de (d2/dx2) d2/dx2(,)

Intégrale (∫) ∫(,,)

Somme (Σ) Σ(,,,)

Résoudre équation (SolveN) SolveN()

Trouver 1 solution (Solve) Solve(,)

Div. Euclidienne, Reste Rmdr

Div. Euclidienne, Quotient Int÷

Simplification I﻿Simp

Valeur min fonct FMin(,,)

Valeur max fonct FMax(,,)

Logarithme (logab) logab(,)

Logarithme (log) log()

Logarithme népérien (ln) ln()

Probabilités

Factorielle (!) !

Permutation (P) P

Combinaison (C) C

Nombre aléatoire (0 à 1) Ran#

Entier aléatoire (n à m) RanInt#(,)

Nombre aléatoire (Normal) RanNorm#(,)

Nombre aléatoire (Binomial) RanBin#(,)

Nb aléatoire dans liste (0 à 1) RanList#()

Échant aléatoire de liste RanSamp#(,)

Calcul numérique

PGCD GCD(,)

PPCM LCM(,)

Valeur absolue Abs()

Partie entière Int()

Partie fractionnaire Frac()

Arrondir Rnd

Partie entière Intg()

Arrondi interne RndFix()

Reste division MOD(,)

Exponentiation modulaire MOD_Exp(,,)

Conversions d’unité

Liste des commandes d’unité

Données variables

Données variables > Statistiques

Statistiques > X

Statistiques > Y

Statistiques > Graphe

Statistiques > PTS

Statistiques > Entrée

Statistiques > Résultat > Test

Statistiques > Résultat > INTR

Données variables > Probabilités

Données variables > Table

Données variables > Récurrence

Données variables > Équation

Vecteur

Vecteur Vct

Produit scalaire DotP(,)

Produit vectoriel CrossP(,)

Angle 2 vecteurs Angle(,)

Vecteur unitaire UnitV()

Norme de vecteur Norm()

Matrice

Matrice Mat

Déterminant Det()

Matrice inverse -1

Transposée Trn()

Matrice identité Identity()

Forme échelonnée Ref()

Forme échelonnée réduite Rref()

Concaténer matrices Augment(,)

Remplir la matrice Fill(,)

Dimensions Dim()

Nombre complexe

Module Abs()

i i

Ir∠θ Ir∠θ

Ia+bi Ia+bi

Argument Arg()

Conjugué Conjg()

Dérivée 2de (d²/dx²) d²/dx²(,)

Simplification ISimp

Matrice inverse ^-1

$i$ $i$

Ia+b $i$ Ia+b $i$

Variance Variance_ $σ^{2}$ () Variance_ $σ^{2}$ ()

Valeur estimée x $\hat{x}$
Valeur estimée y $\hat{y}$

Radians $^{r}$

Grades $^{g}$

Normale(0,1) P(t)=P(X≤t) P()
Normale(0,1) Q(t)=P(0≤X≤t) Q()
Normale(0,1) R(t)=P(X≥t) R()

Densité $χ^{2}$ (x,df) ChiPD(,)

$χ^{2}$ P(a≤X≤b) (a,b,df) ChiCD(,,)

Inverse $χ^{2}$ (p,df) InvChiCD(,)