fx-100MS/fx-570MS/
fx-991MS/
(2nd edition / S-V.P.A.M.)
Before Using the Calculator
Calculation Modes and Calculator Setup
Basic Calculations
- ▶Inputting Expression and Values
- ▶Arithmetic Calculations
- ▶Fraction Calculations
- ▶Percent Calculations
- ▶Degree, Minute, Second (Sexagesimal) Calculations
- ▶Multi-Statements
- ▶Using Engineering Notation
- ▶Using Engineering Symbols
- ▶Calculation History and Replay
- ▶Using Memory Functions
Function Calculations
- ▶Pi (π), Natural Logarithm Base e
- ▶Trigonometric Functions, Inverse Trigonometric Functions
- ▶Hyperbolic Functions, Inverse Hyperbolic Functions
- ▶Angle Unit Conversion
- ▶Exponential Functions, Logarithmic Functions
- ▶Power Functions and Power Root Functions
- ▶Integration Calculations
- ▶Differential Calculations
- ▶Rectangular-Polar Coordinate Conversion
- ▶Factorial (!)
- ▶Random Number (Ran#)
- ▶Permutation (nPr) and Combination (nCr)
- ▶Rounding function (Rnd)
- ▶Using CALC
- ▶Using SOLVE
- ▶Scientific Constants (fx-570MS/fx-991MS only)
- ▶Metric Conversion (fx-570MS/fx-991MS only)
Using Calculation Modes
- ▶Complex Number Calculations (CMPLX)
- ▶Statistical Calculations (SD, REG)
- ▶Base-n Calculations (BASE)
- ▶Equation Calculations (EQN)
- ▶Matrix Calculations (MAT) (fx-570MS/fx-991MS only)
- ▶Vector Calculations (VCT) (fx-570MS/fx-991MS only)
Technical Information
Using SOLVE
SOLVE lets you solve an expression using variable values you want, without the need to transform or simplify the expression.
Note that SOLVE can be used in the COMP Mode only.
Example: To solve y = ax2 + b for x when y = 0, a = 1, and b = -2
(Y)
(=)
(A)
(X) 
(B)
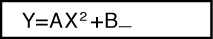
(SOLVE)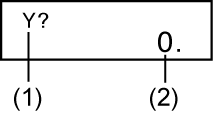
- (1) Prompts for input of a value for Y
(2) Current value of Y
- 0
- 1
- 2
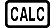- (SOLVE)
- Solution screen
- To exit SOLVE:
Important!
The following functions are not allowed inside of an equation: ∫, d/dx, Pol, Rec.
Depending on what you input for the initial value (solution variable), SOLVE may not be able to obtain solutions. If this happens, try changing the initial value so they are closer to the solution.
SOLVE may not be able to determine the correct solution, even when one exists.
SOLVE uses Newton's method, so even if there are multiple solutions, only one of them will be returned.
Due to limitations in Newton's method, solutions tend to be difficult to obtain for equations like the following: y = sin(x), y = ex, y = √x, y = x-1
If an expression does not include an equals sign (=), SOLVE produces a solution for expression = 0.
