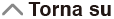Calcoli di integrazione
Funzione per eseguire l'integrazione numerica utilizzando il metodo Gauss-Kronrod.
La sintassi d'introduzione con visualizzazione naturale è ∫ba f (x)dx, mentre la sintassi d'introduzione con visualizzazione lineare è ∫ (f (x), a, b, tol).
tol specifica la tolleranza, che diventa 1 × 10-5 quando non viene introdotto nulla per tol.
Esempio 1: ∫e1 ln(x) = 1
(MthIO-MathO)
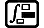

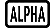
 (X)
(X)
 1
1
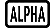
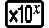 (e)
(e)
- 1
(LineIO)
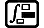

 (X)
(X)
 (,) 1
(,) 1
 (,)
(,)
 (e)
(e)

- 1
Esempio 2: ∫(1x2 , 1, 5, 1 × 10-7) = 0,8 (LineIO)
 1
1
 (X)
(X)
 (,) 1
(,) 1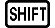
 (,) 5
(,) 5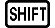
 (,)
(,)
1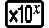
 7
7

- 0,8
Esempio 3: ∫π0 (sin x + cos x)2 dx = π (tol: non specificato) (MthIO-MathO) (unità di misura degli angoli: Rad)
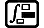


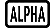
 (X)
(X)


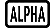
 (X)
(X)


 0
0
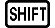
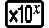 (π)
(π)
- π
Precauzioni sui calcoli dell'integrazione
Il calcolo dell'integrazione può essere eseguito solo in modalità COMP.
Le seguenti opzioni non possono essere utilizzate in f(x), a, b, o tol: Pol, Rec, ∫, d/dx, Σ.
Quando si utilizza una funzione trigonometrica in f(x), specificare Rad come unità di misura degli angoli.
Un valore tol inferiore corrisponde a un aumento della precisione, ma anche il tempo di calcolo aumenta. Quando si specifica tol, utilizzare un valore che sia uguale a 1 × 10-14 o superiore.
L'Integrazione richiede normalmente una quantità di tempo considerevole per l'esecuzione.
A seconda del contenuto di f(x) e della regione d'integrazione, può essere generato un errore di calcolo che supera la tolleranza, che causerà la visualizzazione di un messaggio di errore sulla calcolatrice.
Il contenuto di f(x), i valori positivi/negativi all'interno dell'intervallo di integrazione e l'intervallo da integrare possono determinare un errore importante nei valori di integrazione risultanti. (Esempi: Quando ci sono parti con punti discontinui o cambi improvvisi. Quando l'intervallo di integrazione è troppo ampio.) In tali casi, dividere l'intervallo di integrazione in più parti ed eseguire il calcolo potrebbe migliorare la precisione di calcolo.
Suggerimenti per la riuscita di calcoli di integrazione
Quando una funzione periodica o l'intervallo di integrazione dà come risultato valori di funzione f(x) positivi e negativi
Eseguire integrazioni separate per ogni ciclo, o per la parte positiva e per la parte negativa e poi combinare i risultati.
(1) Parte positiva
(2) Parte negativa
Quando i valori di integrazione fluttuano ampiamente a causa di variazioni minime nell'intervallo di integrazione
Dividere l'intervallo di integrazione in parti multiple (in modo da rompere le aree di ampia fluttuazione in parti piccole), eseguire l'integrazione su ogni parte, quindi combinare i risultati.