Calcoli differenziali
Funzione per l'approssimazione di una derivata basata sul metodo della differenza centrale.
La sintassi d'introduzione con visualizzazione naturale è ddx (f (x)) | x=a, mentre la sintassi d'introduzione con visualizzazione lineare è ddx (f (x), a, tol).
tol specifica la tolleranza, che diventa 1 × 10-10 quando non viene introdotto nulla per tol.
Esempio 1: Per calcolare la derivata nel punto x = π/2 della funzione y = sin(x) (unità di misura degli angoli: Rad)
(MthIO-MathO)
 (
(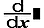 )
)
 (X)
(X)


 (π)
(π) 2
2
- 0
(LineIO)
 (
(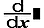 )
)
 (X)
(X)
 (,)
(,)
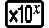 (π)
(π) 2
2

- 0
Esempio 2: ddx (3x2 - 5x + 2, 2, 1 × 10-12) = 7 (LineIO)
 (
(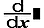 ) 3
) 3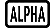
 (X)
(X)
 5
5
 (X)
(X) 2
2
 (,)
(,)
2
 (,) 1
(,) 1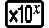
 12
12

- 7
Precauzioni sui calcoli differenziali
Il calcolo differenziale può essere eseguito solo in modalità COMP.
Le seguenti opzioni non possono essere utilizzate in f(x), a, b, o tol: Pol, Rec, ∫, d/dx, Σ.
Quando si utilizza una funzione trigonometrica in f(x), specificare Rad come unità di misura degli angoli.
Un valore tol inferiore corrisponde a un aumento della precisione, ma anche il tempo di calcolo aumenta. Quando si specifica tol, utilizzare un valore che sia uguale a 1 × 10-14 o superiore.
Se non si riesce a trovare una convergenza a una soluzione quando viene omessa l'introduzione di tol, il valore tol verrà regolato automaticamente per determinare la soluzione.
Punti non-consecutivi, fluttuazione discontinua, punti estremamente grandi o piccoli, punti di inflessione, e l'inclusione di punti che non possono essere differenziati o di un punto differenziale o il risultato di un calcolo differenziale che si avvicini a zero, possono causare scarsa precisione o errore.