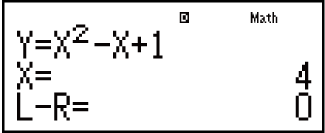CASIO

SOLVE utiliza el método de Newton para aproximar la solución de las ecuaciones.
Observe que la función SOLVE está disponible solo en modo COMP.
A continuación se describen los tipos de ecuaciones cuyas soluciones se pueden obtener con SOLVE.

Ecuaciones que incluyen la variable X: X2 + 2X - 2, Y = X + 5, X = sen(M), X + 3 = B + C
SOLVE busca una solución para X. Una expresión como X2 + 2X - 2 es tratada como X2 + 2X - 2 = 0.

Entrada de ecuaciones con la siguiente sintaxis: {ecuación}, {variable a resolver}
SOLVE busca una solución para Y, por ejemplo, cuando se introduce una ecuación de la siguiente manera: Y = X + 5, Y

Ejemplo: Resolver y = ax2 + b para x cuando y = 0, a = 1, y b = -2

• (Y)(=)
  (A)(X)(B)
• 

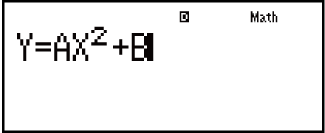
• (SOLVE)
• 

• (1) Solicita la introducción de un valor para Y

  (2) Valor actual de Y

• 012
• 

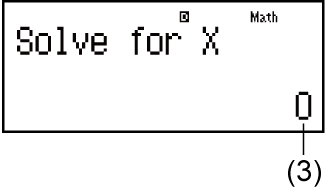
• (3) Valor actual de X

Introducir un valor inicial para X (en este caso, introduzca 1):

• 1
• 

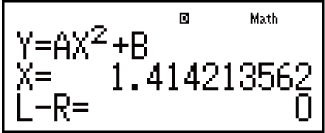
  Pantalla de solución

• Para salir de SOLVE: 

Contenido de la pantalla de soluciones

Las soluciones siempre se visualizan en formato decimal.

      (1) Ecuación (La ecuación introducida.)
      (2) Variable sobre la que se busca una solución
      (3) Solución
      (4) Resultado (lado izquierdo) - (lado derecho)

"Resultado (lado izquierdo) - (lado derecho)" muestra el resultado cuando el lado derecho de la ecuación se resta del lado izquierdo después de asignar el valor obtenido a la variable sobre la que se busca una solución. Cuanto más cercano a cero sea este resultado, mayor precisión tendrá la solución.

Pantalla continua

SOLVE realiza una iteración una cantidad prefijada de veces. Si no puede hallar una solución, muestra una pantalla de confirmación que dice "Continue: [=]", preguntándole si desea continuar.

Presione para continuar o para cancelar la operación SOLVE.

Ejemplo: Resolver y = x2 - x + 1 para x cuando y = 3, 7 y 13.

• (Y)(=)
  (X)(X)1
• 

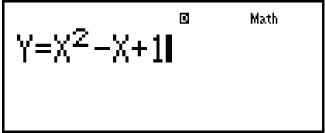
• (SOLVE)
• 

• 3
• 

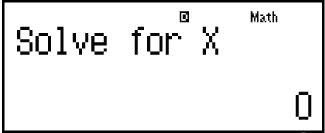
Introducir un valor inicial para X (en este caso, introduzca 1):

• 1
• 

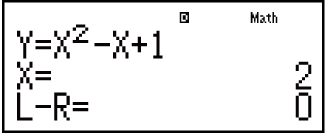
• 7
• 

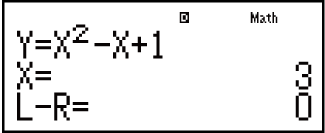
• 13
•