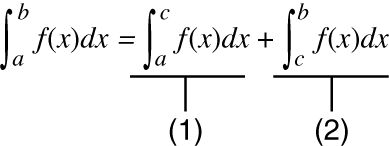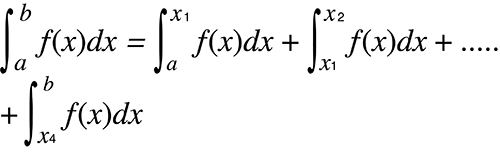Cálculos integrales
Función para realizar una integración numérica mediante el método de Gauss-Kronrod.
La sintaxis de entrada con el display Natural es ∫ba f (x)dx, mientras que con el display Linear es ∫ (f (x), a, b, tol).
tol especifica la tolerancia, que se convierte en 1 × 10-5 cuando no se introduce nada para tol.
Ejemplo 1: ∫e1 ln(x) = 1
(MthIO-MathO)

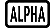
 (X)
(X)
 1
1
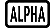
 (e)
(e)
- 1
(LineIO)

 (X)
(X)
 (,) 1
(,) 1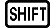
 (,)
(,)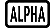
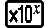 (e)
(e)

- 1
Ejemplo 2: ∫(1x2 , 1, 5, 1 × 10-7) = 0,8 (LineIO)
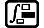 1
1
 (X)
(X)
 (,) 1
(,) 1
 (,) 5
(,) 5
 (,)
(,)
1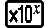
 7
7

- 0,8
Ejemplo 3: ∫π0 (sen x + cos x)2 dx = π (tol: sin especificar) (MthIO-MathO) (unidad de ángulo: Rad)
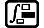


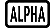
 (X)
(X)


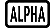
 (X)
(X)


 0
0
 (π)
(π)
- π
Precauciones en el cálculo integral
El cálculo integral puede realizarse solo en modo COMP.
No puede utilizarse en f(x): Pol, Rec, ÷R. No puede utilizarse en f(x), a, b o tol: ∫, d/dx, Σ, Π.
Si utiliza una función trigonométrica en f(x), establezca Rad como unidad de ángulo.
Un valor de tol más pequeño incrementa la precisión, pero incrementa también el tiempo de cálculo. Especifique un valor tol que sea 1 × 10-14 o mayor.
Una integración requiere normalmente considerable tiempo de cálculo.
Dependiendo del contenido de f(x) y de la región de integración, se puede generar el error de cálculo que supera la tolerancia, lo que provoca que la calculadora muestre un mensaje de error.
El contenido de f(x), los valores positivo y negativo dentro del intervalo de integración y el intervalo que desea integrarse pueden generar un gran mensaje de error como resultado de los valores de integración. (Ejemplos: Cuando hay partes con puntos discontinuos o cambios bruscos. Cuando el intervalo de integración es demasiado amplio.) En esos casos, es posible que la precisión del cálculo mejore si se divide el intervalo de integración en partes y se ejecuta el cálculo.
Consejos para el cálculo integral
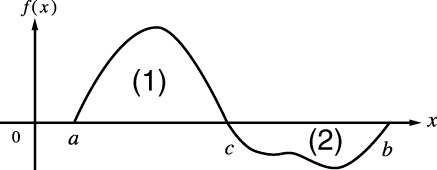
Cuando una función periódica o intervalo de integración da como resultado valores de la función f(x) positivo y negativo
Realice integraciones separadas sobre cada ciclo o la parte positiva y la parte negativa, y luego combine los resultados.
(1) Parte positiva
(2) Parte negativa
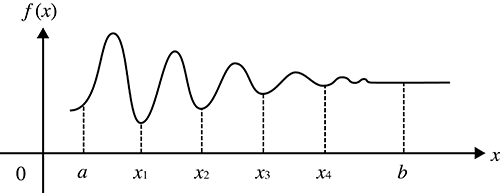
Cuando los valores de integración fluctúan bruscamente debido a desplazamientos muy pequeños en el intervalo de integración
Divida el intervalo de integración en varias partes (de modo que las zonas de gran fluctuación se descompongan en otras más pequeñas), realice la integración en cada parte y luego combine los resultados.