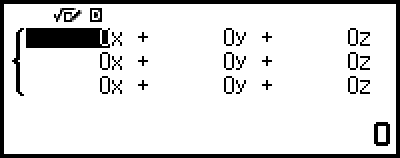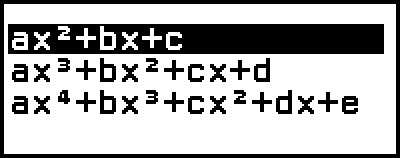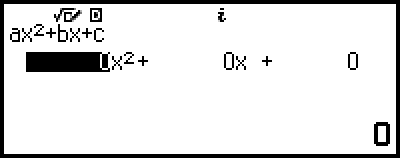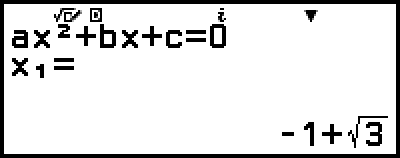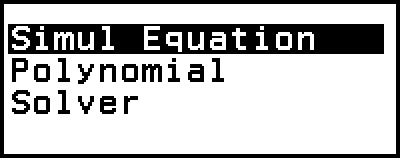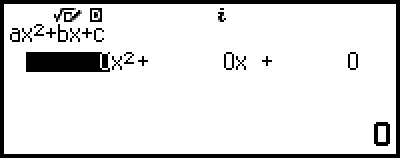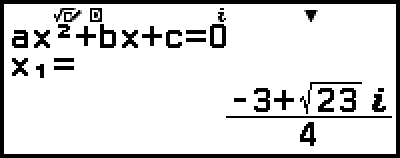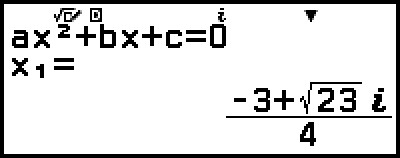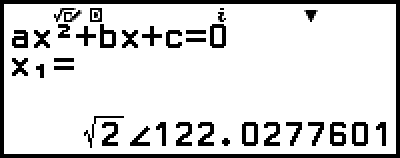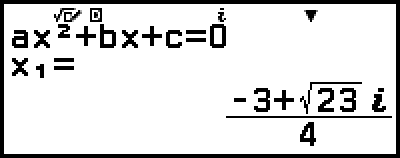حسابات المعادلات
يتضمن تطبيق Equation الدوال الثلاث الموضحة أدناه. بعد بدء تشغيل التطبيق، يمكنك استخدام قائمة Equation التي تظهر لاختيار التي تريدها.
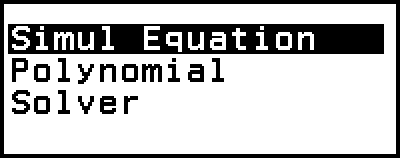
Simul Equation: معادلات خطية متزامنة مع اثنين إلى أربعة مجاهيل
Polynomial: المعادلات عالية الدرجة من الدرجة الثانية إلى الرابعة
Solver: دالة لإيجاد قيمة أي متغير في المعادلة المدخلة
المعادلات الخطية المتزامنة
هنا، نشرح الطريقة العامة لحل معادلة متزامنة بواسطة مثال يحل معادلة خطية متزامنة بثلاثة مجاهيل.
مثال 1: 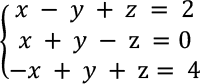
1. اضغط  ، اختر أيقونة التطبيق Equation، ثم اضغط على
، اختر أيقونة التطبيق Equation، ثم اضغط على  .
.
يعرض هذا قائمة Equation.
2. اختر [Simul Equation]، ثم اضغط  .
.
يعرض هذا قائمة عدد المجاهيل.
3. اختر [3 Unknowns]، ثم اضغط  .
.
يعرض هذا محرر المعامل.
4. استخدم محرر المعامل لكي تدخل قيم المعاملات.
- 1


 ((-))1
((-))1 1
1 2
2
1 1
1

 ((-))1
((-))1 0
0

 ((-))1
((-))1 1
1 1
1 4
4
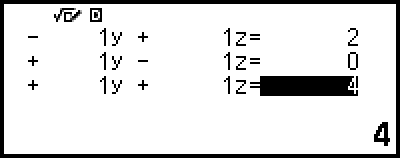
سيؤدي الضغط على  أثناء عرض محرر المعامل إلى مسح جميع المعاملات لتصبح صفراً.
أثناء عرض محرر المعامل إلى مسح جميع المعاملات لتصبح صفراً.
5. اضغط  .
.
هذا سوف يعرض حل.
أثناء عرض المؤشر  ، ستعرض كل ضغطة على
، ستعرض كل ضغطة على  (أو
(أو  ) حلاً آخر.
) حلاً آخر.
 (أو
(أو  )
) 
 (أو
(أو  )
) 
يؤدي الضغط على  أو
أو  أثناء عرض المؤشر
أثناء عرض المؤشر  إلى إعادة إظهار الحل المعروض مسبقًا.
إلى إعادة إظهار الحل المعروض مسبقًا.
يؤدي الضغط على  بينما يكون الحل النهائي معروضاً، إلى العودة إلى محرر المعامل. للعودة إلى محرر المعامل بينما يكون أي حل معروضاً، اضغط
بينما يكون الحل النهائي معروضاً، إلى العودة إلى محرر المعامل. للعودة إلى محرر المعامل بينما يكون أي حل معروضاً، اضغط  .
.
يؤدي الضغط على  أثناء عرض محرر المعامل إلى العودة إلى قائمة عدد المجاهيل.
أثناء عرض محرر المعامل إلى العودة إلى قائمة عدد المجاهيل.
ملاحظة
أثناء عرض محرر المعامل، يمكنك تخزين القيمة المظللة حاليًا إلى متغير. أيضًا، أثناء ما يكون الحل معروضاً، يمكن تخزين الحل المعروض حاليًا إلى متغير. للحصول على تفاصيل حول المتغيرات، راجع "المتغيرات (A، B، C، D، E، F، x، y، z)".
المعادلات عالية الدرجة من الدرجة الثانية إلى الرابعة
عند حل معادلة عالية الدرجة باستخدام تطبيق Equation، يتم عرض القيم أدناه وفقًا لدرجة المعادلة.
المعادلة التربيعية
بعد عرض الحل لـ ax2+bx+c=0، يتم عرض الإحداثيات الدنيا (أو القصوى) (x، y) لـ y=ax2+bx+c.
المعادلة التكعيبية
بعد عرض الحل لـ ax3+bx2+cx+d=0، يتم عرض الإحداثيات (x، y) للقيمة الدنيا المحلية (أو القيمة القصوى المحلية) لـ y=ax3+bx2+cx+d، فقط إذا كان توجد قيمة دنيا محلية أو قيمة قصوى محلية. في حالة عدم وجود قيمة دنيا محلية أو قيمة قصوى محلية، سيؤدي الضغط على  أثناء عرض الحل الأخير إلى ظهور الرسالة "No Local Max/Min".
أثناء عرض الحل الأخير إلى ظهور الرسالة "No Local Max/Min".
المعادلة من الدرجة الرابعة
يتم عرض حل لـ ax4+bx3+cx2+dx+e=0.
سنعرض هنا مثالاً لمعادلة تربيعية لشرح الطريقة العامة لحل معادلة عالية الدرجة.
مثال 2: x2 + 2x − 2 = 0
(Input/Output: MathI/MathO)
1. اضغط  ، اختر أيقونة التطبيق Equation، ثم اضغط على
، اختر أيقونة التطبيق Equation، ثم اضغط على  .
.
يعرض هذا قائمة Equation.
2. اختر [Polynomial]، ثم اضغط على  .
.
يعرض هذا قائمة عدد الدرجات.
3. اختر [ax2+bx+c]، ثم اضغط  .
.
يعرض هذا محرر المعامل.
4. استخدم محرر المعامل لكي تدخل قيم المعاملات.
- 1
 2
2

 ((-))2
((-))2
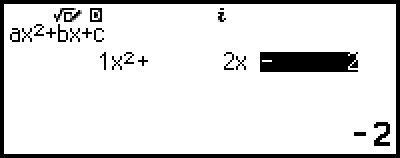
سيؤدي الضغط على  أثناء عرض محرر المعامل إلى مسح جميع المعاملات لتصبح صفراً.
أثناء عرض محرر المعامل إلى مسح جميع المعاملات لتصبح صفراً.
5. اضغط  .
.
هذا سوف يعرض حل.
أثناء عرض المؤشر  ، ستعرض كل ضغطة على
، ستعرض كل ضغطة على  (أو
(أو  ) نتيجة حساب أخرى (حل أو إحداثي).
) نتيجة حساب أخرى (حل أو إحداثي).
 (أو
(أو  )
) 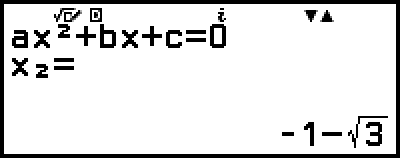
(يعرض الإحداثي-x للقيمة الدنيا لـ y = x2 + 2x − 2.)
 (أو
(أو  )
) 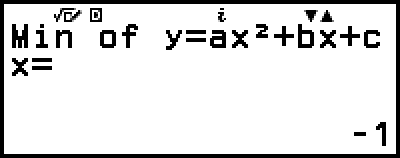
(يعرض الإحداثي-y للقيمة الدنيا لـ y = x2 + 2x − 2.)
 (أو
(أو  )
)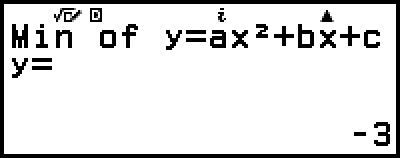
يؤدي الضغط على  أو
أو  أثناء عرض المؤشر
أثناء عرض المؤشر  إلى ظهور نتيجة الحساب المعروضة مسبقًا مرة أخرى.
إلى ظهور نتيجة الحساب المعروضة مسبقًا مرة أخرى.
يؤدي الضغط على  أثناء عرض نتيجة الحساب النهائي إلى العودة إلى محرر المعامل. للعودة إلى محرر المعامل بينما يكون أي نتيجة حساب معروضاً، اضغط
أثناء عرض نتيجة الحساب النهائي إلى العودة إلى محرر المعامل. للعودة إلى محرر المعامل بينما يكون أي نتيجة حساب معروضاً، اضغط  .
.
يؤدي الضغط على  أثناء عرض محرر المعامل إلى العودة إلى قائمة عدد الدرجات.
أثناء عرض محرر المعامل إلى العودة إلى قائمة عدد الدرجات.
ملاحظة
أثناء عرض محرر المعامل، يمكنك تخزين القيمة المظللة حاليًا إلى متغير. أيضًا، أثناء عرض نتيجة الحساب (الحل أو الإحداثي)، يمكن تخزينها إلى متغير. للحصول على تفاصيل حول المتغيرات، راجع "المتغيرات (A، B، C، D، E، F، x، y، z)".
عرض حل الأعداد المركبة (Complex Roots)
قد تحتوي المعادلات عالية الدرجة على حلول ذات أعداد مركبة. عند اختيار Polynomial في قائمة Equation، يمكنك استخدام العمليات أدناه لتفعيل أو تعطيل عرض الحلول ذات الأعداد المركبة.
 – [Complex Roots] > [On]
– [Complex Roots] > [On] 
يقوم بتفعيل عرض حل ذي عدد مركب (الضوابط الافتراضية الأولية).
 – [Complex Roots] > [Off]
– [Complex Roots] > [Off] 
يقوم بتعطيل عرض حل ذي عدد مركب. سيؤدي إدخال وحل معادلة تحتوي على حل واحد أو أكثر من الحلول ذات الأعداد المركبة فقط إلى ظهور الرسالة "No Real Roots".
مثال 3: 2x2 + 3x + 4 = 0
(Input/Output: MathI/MathO، Complex Result: a+bi، Complex Roots: On)
1. اضغط  ، اختر أيقونة التطبيق Equation، ثم اضغط على
، اختر أيقونة التطبيق Equation، ثم اضغط على  .
.
يعرض هذا قائمة Equation.
2. اختر [Polynomial] > [ax2+bx+c].
يعرض هذا محرر المعامل.
3. استخدم محرر المعامل لكي تدخل قيم المعاملات.
- 2
 3
3 4
4

4. اضغط  .
.
هذا سوف يعرض حل.
5. قم بعرض قيم أخرى لحل أو إحداثيات.
 (أو
(أو  )
) 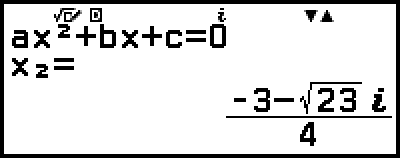
 (أو
(أو  )
) 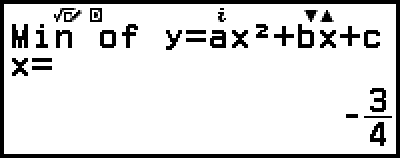
 (أو
(أو  )
)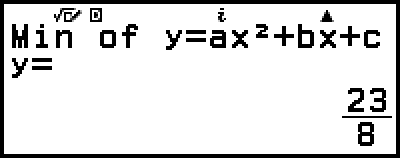
يؤدي الضغط على  أثناء عرض نتيجة الحساب النهائي إلى العودة إلى محرر المعامل. للعودة إلى محرر المعامل بينما يكون أي نتيجة حساب معروضاً، اضغط
أثناء عرض نتيجة الحساب النهائي إلى العودة إلى محرر المعامل. للعودة إلى محرر المعامل بينما يكون أي نتيجة حساب معروضاً، اضغط  .
.
تحويل حل ذي عدد مركب إلى إحداثيات متعامدة أو قطبية
يمكنك استخدام قائمة FORMAT التي تظهر عند الضغط على  لتحويل حل ذي عدد مركب إلى تنسيق إحداثيات متعامدة أو قطبية.
لتحويل حل ذي عدد مركب إلى تنسيق إحداثيات متعامدة أو قطبية.
مثال 4: لتحويل الحل ذي العدد المركب المعروض في المثال 3 إلى تنسيق إحداثيات قطبية ثم إلى تنسيق إحداثيات متعامدة
1. نفذ الخطوات من 1 إلى 4 من المثال 3.
2. اضغط  ، اختر [Polar Coord]، ثم اضغط
، اختر [Polar Coord]، ثم اضغط  .
.
هذا يحول الحل إلى تنسيق إحداثيات قطبية.
3. اضغط  ، اختر [Rectangular Coord]، ثم اضغط
، اختر [Rectangular Coord]، ثم اضغط  .
.
هذا يحول الحل إلى تنسيق إحداثيات متعامدة.
استخدام Solver
يستخدم Solver طريقة نيوتن لتقريب حل المعادلات. يدعم Solver إدخال المعادلات بالتنسيقات التالية.
أمثلة: x = sin(A) ،y = x + 5، xy + C(يتم معاملتها كـ xy + C = 0)
مثال 5: لحل x2 - B2 = 0 لـ x عندما B = 4
(Input/Output: MathI/MathO)
ملاحظة
قبل حل x2 - B2 = 0 لـ x، يجب تخزين 4 إلى المتغير B. ويتم ذلك في الخطوة 3 من الطريقة أدناه.
1. اضغط  ، اختر أيقونة التطبيق Equation، ثم اضغط على
، اختر أيقونة التطبيق Equation، ثم اضغط على  .
.
يعرض هذا قائمة Equation.
2. اختر [Solver]، ثم اضغط  .
.
يعرض هذا شاشة إدخال معادلة Solver.
3. هنا، قم بتخزين 4 إلى المتغير B.
 4
4

يمكن تنفيذ هذه العملية في أي وقت قبل الخطوة 7 من هذا الإجراء.
للحصول على تفاصيل حول المتغيرات، راجع "المتغيرات (A، B، C، D، E، F، x، y، z)".
اضغط  للعودة إلى شاشة إدخال معادلة Solver.
للعودة إلى شاشة إدخال معادلة Solver.
4. أدخل المعادلة.



 (B)
(B) 2
2

 (=)*0
(=)*0
* يمكنك أيضًا استخدام العملية التالية لإدخال علامة =:  – [Equation] > [=].
– [Equation] > [=].
5. اضغط  لتسجيل المعادلة المدخلة.
لتسجيل المعادلة المدخلة.
6. في شاشة Solve Target التي تظهر، تأكد من اختيار [x] ثم اضغط  .
.
يعرض هذا شاشة بالقيمة الابتدائية لـ x.
7. أدخل 1 كقيمة ابتدائية لـ x.
- 1


8. بعد التأكد من اختيار [Execute]، اضغط  لحل المعادلة.
لحل المعادلة.
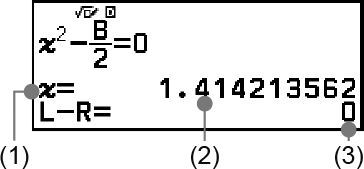
(1) المتغير الذي يتم الحل من أجله
(2) الحل
(3) نتيجة (الجانب الأيسر) - (الجانب الأيمن)
دائما يتم عرض الحلول في التشكيل العشري.
كلما كانت نتيجة (الجانب الأيسر) - (الجانب الأيمن) أقرب إلى الصفر، كانت دقة الحل أعلى.
9. بعد ذلك، اضغط المفتاح الذي يقوم بإجراء العملية التي تريدها.
| للقيام بهذا: | اضغط هذا المفتاح: |
|---|---|
| قم بالعودة إلى الشاشة في الخطوة 6. |  * * |
| قم بتخزين التعبير الرياضي المدخل والعودة إلى الشاشة في الخطوة 4. |  أو أو  |
* تصبح القيمة الابتدائية عند ضغط هذا المفتاح هي القيمة الابتدائية التي استخدمتها آخر مرة في الحساب.
هام!
-
يقوم Solver بالتقارب لعدد مرات مضبوطة مسبقًا. إذا لم يستطع إيجاد حل ما، فإنه يعرض شاشة تأكيد مثل تلك المجاورة، تسأل إذا كنت ترغب في الاستمرار. اضغط
 بينما يكون [Continue] مختاراً للمتابعة أو اختر [Exit] ثم
بينما يكون [Continue] مختاراً للمتابعة أو اختر [Exit] ثم  لإلغاء عملية تشغيل Solver.
لإلغاء عملية تشغيل Solver. 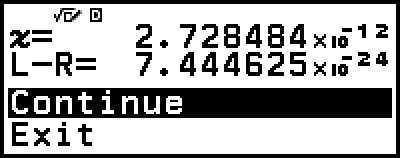
اعتماداً على ما الذي تقوم بإدخاله للقيمة الابتدائية الخاصة بمتغير الحل (x في المثال أعلاه)، قد يكون Solver غير قادر على الحصول على حل. إذا حدث هذا، حاول تغيير القيمة الابتدائية بحيث تكون قريبة للحل.
قد يكون Solver غير قادر على تحديد الحل الصحيح، حتى عندما يوجد أحد الحلول.
يستخدم Solver طريقة نيوتن، لذلك حتى إذا كانت هناك حلول متعددة، واحد منها فقط سوف يستعاد.
نتيجة لحدود أسلوب نيوتن، فإن الحلول تميل إلى أن تكون صعبة في الحصول على معادلات مثل الآتية: y=sinx، y=ex، y=√x.