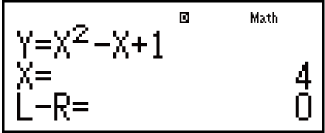Korzystanie z funkcji SOLVE
Funkcja SOLVE wykorzystuje metodę Newtona do określania rozwiązań przybliżonych równań.
Zauważ, że funkcji SOLVE można używać tylko w trybie COMP.
Poniżej opisane są typy równań, których rozwiązania można uzyskać przy użyciu SOLVE.
Równania zawierające zmienną X: X2 + 2X - 2, Y = X + 5, X = sin(M), X + 3 = B + C
SOLVE umożliwia obliczenie X. Wyrażenie X2 + 2X - 2 jest traktowane jako X2 + 2X - 2 = 0.
Wprowadzanie równań przy użyciu następującej składni: {equation}, {solution variable}
SOLVE umożliwia obliczenie Y, gdy przykładowo równanie jest wprowadzone jako: Y = X + 5, Y
Ważne!
Jeżeli równanie zawiera wprowadzone funkcje, które obejmują otwarte nawiasy (takie jak sin i log), pamiętaj o zamknięciu nawiasu.
Następujące funkcje nie są dozwolone wewnątrz równania: ∫, d/dx, Σ, Pol, Rec.
Przykład: Aby rozwiązać równanie y = ax2 + b i obliczyć x, gdy y = 0, a = 1 i b = -2
 (Y)
(Y)
 (=)
(=)
 (A)
(A)
 (X)
(X)

 (B)
(B)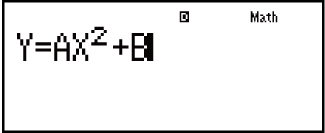
 (SOLVE)
(SOLVE)
(1) Podpowiedź, jak wprowadzić wartość Y
(2) Bieżąca wartość Y
- 0
 1
1
 2
2
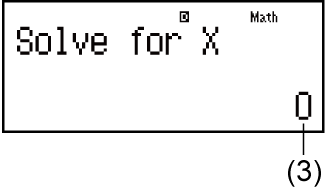
(3) Bieżąca wartość X
Wprowadź wartość początkową X (tutaj wprowadź 1):
- 1

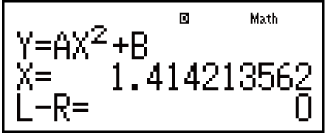
Ekran rozwiązania
- Aby zamknąć funkcję SOLVE:

Uwaga
Od momentu naciśnięcia klawisza 
 (SOLVE) aż do zamknięcia funkcji SOLVE przez naciśnięcie klawisza
(SOLVE) aż do zamknięcia funkcji SOLVE przez naciśnięcie klawisza  powinno się używać procedur wprowadzania wyświetlania liniowego dla wprowadzania danych.
powinno się używać procedur wprowadzania wyświetlania liniowego dla wprowadzania danych.
Ważne!
Zależnie od wprowadzonej wartości początkowej zmiennej X (zmienna rozwiązania), funkcja SOLVE może nie być w stanie uzyskać rozwiązań. Jeżeli tak się zdarzy, spróbuj zmienić wartość początkową, tak aby była bliższa rozwiązaniu.
Funkcja SOLVE może nie być w stanie określić prawidłowego rozwiązania, nawet wtedy gdy takie istnieje.
Ze względu na wykorzystywanie metody Newtona funkcja SOLVE zwróci tylko jedno rozwiązanie, nawet jeżeli jest ich wiele.
Z powodu ograniczeń metody Newtona, trudno jest uzyskać rozwiązania równań podobnych do następujących: y = sin(x), y = ex, y = √x.
Zawartość ekranu rozwiązania
Rozwiązania są zawsze wyświetlane w formacie dziesiętnym.

(1) Równanie (wprowadzone równanie)
(2) Zmienna obliczana
(3) Rozwiązanie
(4) Wynik (lewa strona) – (prawa strona)
„Wynik (lewa strona) – (prawa strona)” pokazuje wynik, kiedy prawa strona równania zostanie odjęta od lewej strony, po przypisaniu uzyskanej wartości zmiennej, dla której było przeprowadzane rozwiązanie. Im wynik jest bliższy zeru, tym wyższa jest dokładność rozwiązania.
Ekran kontynuacji
Funkcja SOLVE wykonuje zbieżność określoną ilość razy. Jeżeli nie może znaleźć rozwiązania, wyświetlany jest ekran potwierdzający z monitem „Continue: [=]” o potwierdzenie kontynuowania.
Naciśnij klawisz  , aby kontynuować, lub
, aby kontynuować, lub  , aby anulować operację SOLVE.
, aby anulować operację SOLVE.
Przykład: Aby rozwiązać równanie y = x2 - x + 1 i obliczyć x, gdy y = 3, 7 i 13.
 (Y)
(Y)
 (=)
(=)
 (X)
(X)

 (X)
(X) 1
1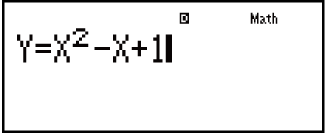
 (SOLVE)
(SOLVE)
- 3

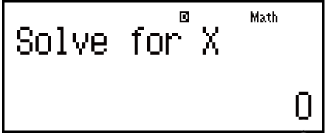
Wprowadź wartość początkową X (tutaj wprowadź 1):
- 1

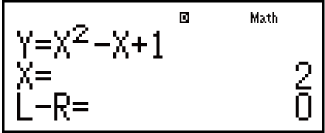
 7
7

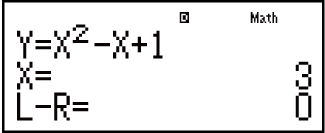
 13
13