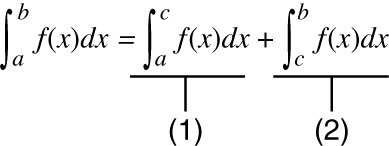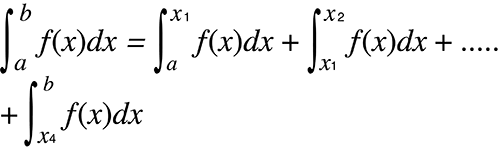Integrálszámítások
Függvény, amellyel numerikus integrálás végezhető a Gauss-Kronrod módszer alkalmazásával.
A természetes kijelzés bevitelének szintakszisa ∫ba f (x)dx, míg a lineáris kijelző bevitelének szintakszisa ∫ (f (x), a, b, tol).
A tol megadja a tűrést, ami 1 × 10-5 lesz, ha semmit sem ad meg a tol értékének.
1. példa: ∫e1 ln(x) = 1
(MthIO-MathO)

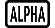
 (X)
(X)
 1
1
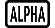
 (e)
(e)
- 1
(LineIO)

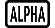
 (X)
(X)

 (,) 1
(,) 1
 (,)
(,)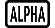
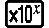 (e)
(e)

- 1
2. példa: ∫(1x2 , 1, 5, 1 × 10-7) = 0,8 (LineIO)
 1
1
 (X)
(X)

 (,) 1
(,) 1
 (,) 5
(,) 5
 (,)
(,)
1
 7
7

- 0,8
3. példa: ∫π0 (sin x + cos x)2 dx = π (tol: Nincs meghatározva) (MthIO-MathO) (Szög mértékegység: Rad)


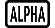
 (X)
(X)


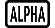
 (X)
(X)


 0
0

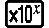 (π)
(π)
- π
Integrálszámítással kapcsolatos óvintézkedések
Integrálszámításokat csak a COMP módban lehet elvégezni.
Az alábbiak nem használhatók az f(x), a, b, és tol esetében: Pol, Rec, ∫, d/dx, Σ.
Amikor az f(x) esetében trigonometrikus függvényt használ, szög mértékegységként „Rad”-ot adjon meg.
A kisebb tol érték növeli a pontosságot, de növeli a számítási időt is. A tol megadásakor 1 × 10-14 vagy nagyobb értéket használjon.
Az integrálás elvégzése általában jelentős nagyságú időt vesz igénybe.
A f(x) tartalmától és az integrálási tartománytól függően olyan számítási hiba állhat elő, amely meghaladja a tűrést és így a számológép hibaüzenetet fog kijelezni.
A f(x) tartalma, a pozitív/negatív értékek az integrálási intervallumon belül, és az integrálandó intervallum nagy hibát okozhat az eredményül kapott integrációs értékekben. (Példák: Ha vannak olyan részek, amelyeknek szakaszos pontjai vagy hirtelen változásai vannak. Ha az integrálási intervallum túl széles.) Ilyen esetekben az integrálási intervallum részekre osztása és a számítás végrehajtása javíthatja a számítási pontosságot.
Ötletek az integrálszámítások sikeres elvégzéséhez
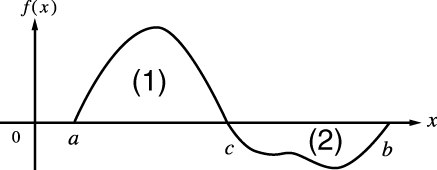
Amikor valamelyik periodikus függvény vagy integrálási intervallum pozitív és negatív f(x) függvényértékeket eredményez
Mindegyik ciklusnál, vagy a pozitív és negatív résznél végezzen külön integrálásokat és azután egyesítse az eredményeket.
(1) Pozitív rész
(2) Negatív rész
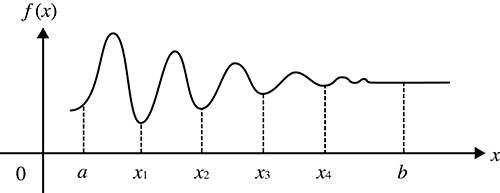
Amikor az integrálási intervallumban mutatkozó parányi eltolódások miatt az integrálási értékek tág határok között ingadoznak
Az integrálási intervallumot több részre kell osztani (oly módon, hogy kis részekre törje a széles ingadozásokat), végezzen integrálást minden egyes részen, majd egyesítse az eredményeket.