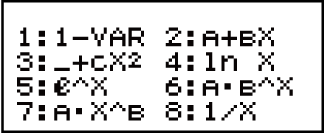
Statisztikai számítások (STAT)
Statisztikai számítás elkezdéséhez végezze el a 
 (STAT) gomb műveletet, hogy belépjen a STAT módba és utána a megjelenő kép használatával válassza ki az elvégezni kívánt számítás típusát.
(STAT) gomb műveletet, hogy belépjen a STAT módba és utána a megjelenő kép használatával válassza ki az elvégezni kívánt számítás típusát.
Az ilyen típusú statisztikai számítás kiválasztásához: (a regressziós képlet zárójelben van) |
Nyomja meg ezt a gombot: |
|---|---|
| Egy változós (X) |  (1-VAR) (1-VAR) |
| Két változós (X, Y), lineáris regresszió (y = A + Bx) |
 (A+BX) (A+BX) |
| Két változós (X, Y), négyzetes regresszió (y = A + Bx + Cx2) |
 (_+CX2) (_+CX2) |
| Két változós (X, Y), logaritmikus regresszió (y = A + Blnx) |
 (ln X) (ln X) |
| Két változós (X, Y), e exponenciális regresszió (y = A eBx) |
 (e∧X) (e∧X) |
| Két változós (X, Y), ab exponenciális regresszió (y = ABx) |
 (A•B∧X) (A•B∧X) |
| Két változós (X, Y), hatványfüggvényes regresszió (y = AxB) |
 (A•X∧B) (A•X∧B) |
| Két változós (X, Y), inverz regresszió (y = A + B/x) |
 (1/X) (1/X) |
A fenti gombok ( -
-  ) bármelyikének megnyomása megjeleníti a Statisztikai szerkesztőt.
) bármelyikének megnyomása megjeleníti a Statisztikai szerkesztőt.
Megjegyzés
Ha át akarja kapcsolni a számítás típusát, miután belépett a STAT módba, a 
 (STAT)
(STAT) (Type) gombművelet elvégzésével jelenítse meg a számítási típus kiválasztására szolgáló képet.
(Type) gombművelet elvégzésével jelenítse meg a számítási típus kiválasztására szolgáló képet.
Adatok bevitele
Adatok beviteléhez használja a Statisztikai szerkesztőt. A Statisztikai szerkesztő megjelenítéséhez végezze el az alábbi gomb műveletet: 
 (STAT)
(STAT) (Data).
(Data).
A Statisztikai szerkesztő 80 sornyi adat bevitelét teszi lehetővé, ha csak X oszlop van, X és FREQ vagy X és Y oszlopok esetén 40 sornyi, X, Y és FREQ oszlop esetén 26 sornyi adat vihető be.
Megjegyzés
Adott számú (gyakoriságú) azonos adattételek beviteléhez használja a FREQ (gyakoriság) oszlopot. A FREQ oszlop kijelzését a beállító menü Stat formátum beállítási értékeinek használatával tudja bekapcsolni (van kijelzés) vagy kikapcsolni (nincs kijelzés).
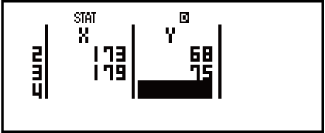
1. példa: Lineáris regresszió kiválasztása és a következő adatok bevitele: (170, 66), (173, 68), (179, 75)

 (STAT)
(STAT) (A+BX)
(A+BX)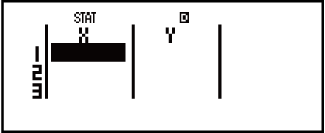
- 170
 173
173 179
179


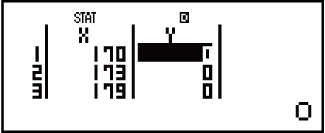
- 66
 68
68 75
75
Fontos!
A Statisztikai szerkesztőben jelenleg tárolt összes adat törlődik, amikor kilép a STAT módból, egy változósról két változós statisztika számítási típusra kapcsol át vagy megváltoztatja a Stat formátum beállított értékét a beállító menün.
A Statisztikai szerkesztő nem támogatja az alábbi műveleteket:  ,
, 
 (M-),
(M-), 
 (STO). Ugyanígy a Pol, Rec és a többtagú kifejezések sem vihetők be a Statisztikai szerkesztővel.
(STO). Ugyanígy a Pol, Rec és a többtagú kifejezések sem vihetők be a Statisztikai szerkesztővel.
Így tudja megváltoztatni egy rekesz adatát:
A Statisztikai szerkesztőben vigye rá a kurzort arra a rekeszre, amely a megváltoztatni óhajtott adatot tartalmazza, vigye be az új adatot, és utána nyomja meg a  -t.
-t.
Sor törlése:
A Statisztikai szerkesztőben vigye rá a kurzort arra a sorra, amelyet ki óhajt törölni, és utána nyomja meg az  -t.
-t.
Sor beillesztése:
A Statisztikai szerkesztőben vigye rá a kurzort arra a helyre, ahol be óhajtja szúrni a sort, és végezze el az alábbi gomb műveletet:

 (STAT)
(STAT) (Edit)
(Edit) (Ins).
(Ins).
A Statisztikai szerkesztő minden tartalmának törlése:
A Statisztikai szerkesztőben végezze el az alábbi gombműveletet:

 (STAT)
(STAT) (Edit)
(Edit) (Del-A).
(Del-A).
Statisztikai számítás képernyő
A Statisztikai számítás képernyő a Statisztikai szerkesztővel bevitt adatok statisztikai számításainak végrehajtására szolgál. A Statisztikai szerkesztő képernyő megjelenítésekor a  gomb megnyomására a Statisztikai számítások képernyőre vált.
gomb megnyomására a Statisztikai számítások képernyőre vált.
A Statisztika menü használata
Miközben a statisztikai számítások képernyő látható a képernyőn, nyomja meg a 
 (STAT) gombot a Statisztikai menü megjelenítéséhez.
(STAT) gombot a Statisztikai menü megjelenítéséhez.
A Statisztikai menü tartalma attól függ, hogy a jelenleg kiválasztott statisztikai művelet típusa egy változót vagy két változós használ-e.
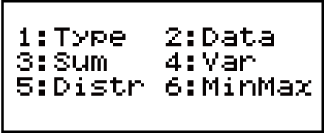
Egy változós statisztika
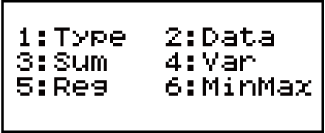
Két változós statisztika
Statisztikai menüelemek
Közös elemek
| Válassza ki ezt a menüelemet: | Ennek megkapásához: |
|---|---|
 (Type) (Type) |
Megjeleníti a számítási típus kiválasztására szolgáló képet |
 (Data) (Data) |
Megjeleníti a Statisztikai szerkesztőt |
 (Sum) (Sum) |
Megjeleníti a parancsok Sum almenüt az összegek számításához |
 (Var) (Var) |
Megjeleníti a parancsok Var almenüt a statisztikai közép, mérvadó eltérés, stb. kiszámításához. |
Egy változós:  (Distr) (Distr) |
Megjeleníti a parancsok Distr almenüt a normál eloszlási számításokhoz • További információkat lásd a „Normális eloszlással kapcsolatos számítások” című részben. |
Két változós:  (Reg) (Reg) |
Megjeleníti a parancsok Reg almenüt a regressziós számításokhoz • Részletekért lásd „Parancsok a Lineáris regressziós számítások (A+BX) kiválasztása esetén” és a „Parancsok a négyzetes regressziós számítások (_+CX2) kiválasztása esetén” című részeket. |
 (MinMax) (MinMax) |
Megjeleníti a parancsok MinMax almenüjét a maximum és minimum értékek megkapásához |
Egy változós (1-VAR) statisztikai számítás parancsok
Sum almenü (
 (STAT)
(STAT) (Sum))
(Sum))
| Válassza ki ezt a menüelemet: | Ennek megkapásához: |
|---|---|
 (∑x2) (∑x2) |
A mintaadatok négyzetének összege |
 (∑x) (∑x) |
A mintaadatok összege |
Var almenü (
 (STAT)
(STAT) (Var))
(Var))
| Válassza ki ezt a menüelemet: | Ennek megkapásához: |
|---|---|
 (n) (n) |
Minták száma |
 (x) (x) |
A mintaadatok statisztikai közepe |
 (σx) (σx) |
Sokaság mérvadó eltérése |
 (sx) (sx) |
Minta mérvadó eltérése |
Distr almenü (
 (STAT)
(STAT) (Distr))
(Distr))
 (P() (P() |
Ez a menü használható a standardizált normális eloszlás valószínűségének kiszámításához. • Részleteket lásd a „Normális eloszlással kapcsolatos számítások” című részben. |
 (Q() (Q() |
|
 (R() (R() |
|
 ( ( t) t) |
MinMax almenü (
 (STAT)
(STAT) (MinMax))
(MinMax))
| Válassza ki ezt a menüelemet: | Ennek megkapásához: |
|---|---|
 (minX) (minX) |
Minimális érték |
 (maxX) (maxX) |
Maximális érték |
Parancsok a Lineáris regressziós számítások (A+BX) kiválasztása esetén
Sum almenü (
 (STAT)
(STAT) (Sum))
(Sum))
| Válassza ki ezt a menüelemet: | Ennek megkapásához: |
|---|---|
 (∑x2) (∑x2) |
Az X-adatok négyzetének összege |
 (∑x) (∑x) |
Az X-adatok összege |
 (∑y2) (∑y2) |
Az Y-adatok négyzetének összege |
 (∑y) (∑y) |
Az Y-adatok összege |
 (∑xy) (∑xy) |
Az X-adatok és az Y-adatok termékeinek négyzetének összege |
 (∑x3) (∑x3) |
Az X-adatok köbének összege |
 (∑x2y) (∑x2y) |
Az (X-adatok négyzete × Y-adatok) összege |
 (∑x4) (∑x4) |
Az X-adatok biquadrate összege |
Var almenü (
 (STAT)
(STAT) (Var))
(Var))
| Válassza ki ezt a menüelemet: | Ennek megkapásához: |
|---|---|
 (n) (n) |
Minták száma |
 (x) (x) |
Az X-adatok statisztikai közepe |
 (σx) (σx) |
Az X-adatok sokaság mérvadó eltérése |
 (sx) (sx) |
Az X-adatok minta mérvadó eltérése |
 (y) (y) |
Az Y-adatok statisztikai közepe |
 (σy) (σy) |
Az Y-adatok sokaság mérvadó eltérése |
 (sy) (sy) |
Az Y-adatok minta mérvadó eltérése |
Reg almenü (
 (STAT)
(STAT) (Reg))
(Reg))
| Válassza ki ezt a menüelemet: | Ennek megkapásához: |
|---|---|
 (A) (A) |
Regressziós tényező állandó kifejezés A |
 (B) (B) |
Regressziós tényező B |
 (r) (r) |
Korrelációs együttható r |
 (xˆ) (xˆ) |
X becsült értéke |
 (yˆ) (yˆ) |
Y becsült értéke |
MinMax almenü (
 (STAT)
(STAT) (MinMax))
(MinMax))
| Válassza ki ezt a menüelemet: | Ennek megkapásához: |
|---|---|
 (minX) (minX) |
Az X-adatok minimális értéke |
 (maxX) (maxX) |
Az X-adatok maximális értéke |
 (minY) (minY) |
Az Y-adatok minimális értéke |
 (maxY) (maxY) |
Az Y-adatok maximális értéke |
Parancsok a négyzetes regressziós számítások (_+CX2) kiválasztása esetén
Reg almenü (
 (STAT)
(STAT) (Reg))
(Reg))
| Válassza ki ezt a menüelemet: | Ennek megkapásához: |
|---|---|
 (A) (A) |
Regressziós tényező állandó kifejezés A |
 (B) (B) |
A regressziós tényezők B lineáris koefficiense |
 (C) (C) |
A regressziós tényezők C négyzetes koefficiense |
 (xˆ1) (xˆ1) |
x1 becsült értéke |
 (xˆ2) (xˆ2) |
x2 becsült értéke |
 (yˆ) (yˆ) |
y becsült értéke |
Megjegyzés
xˆ, xˆ1, xˆ2 és yˆ nem változók. Olyan típusú parancsok, amelyek közvetlenül az előttük lévő argumentumot veszik. További részletek a „Becsült értékek számítása” című részben olvashatók.
2. példa: Így tud bevinni egy változós adatokat x = {1, 2, 2, 3, 3, 3, 4, 4, 5} a FREQ oszlop használatával, ahol meg tudja adni az egyes tételek ismétlési számát ({xn; freqn} = {1;1, 2;2, 3;3, 4;2, 5;1}), és ki tudja számítani a statisztikai közepet és a sokaság mérvadó eltérését.

 (SETUP)
(SETUP)
 (STAT)
(STAT) (ON)
(ON)

 (STAT)
(STAT) (1-VAR)
(1-VAR)
1 2
2 3
3 4
4 5
5


1 2
2 3
3 2
2
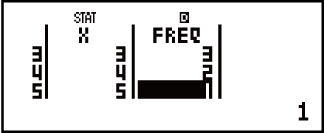


 (STAT)
(STAT) (Var)
(Var) (x)
(x)
- 3


 (STAT)
(STAT) (Var)
(Var) (σx)
(σx)
- 1,154700538
Eredmények: Statisztikai közép: 3, Sokaság mérvadó eltérése: 1,154700538
3. példa: Így tudja kiszámítani a lineáris regressziós és logaritmikus regressziós korrelációs együtthatókat az alábbi két változós adatoknál és meghatározni a regressziós képletet a legerősebb korrelációnál: (x, y) = (20, 3150), (110, 7310), (200, 8800), (290, 9310). Adja meg a Fix 3 (három tizedesjegy) opciót az eredményekhez.

 (SETUP)
(SETUP)
 (STAT)
(STAT) (OFF)
(OFF)

 (SETUP)
(SETUP) (Fix)
(Fix)

 (STAT)
(STAT) (A+BX)
(A+BX)
20 110
110 200
200 290
290


3150 7310
7310 8800
8800 9310
9310
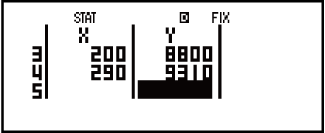


 (STAT)
(STAT) (Reg)
(Reg) (r)
(r)
- 0,923


 (STAT)
(STAT) (Type)
(Type) (ln X)
(ln X)


 (STAT)
(STAT) (Reg)
(Reg) (r)
(r)
- 0,998


 (STAT)
(STAT) (Reg)
(Reg) (A)
(A)
- -3857,984


 (STAT)
(STAT) (Reg)
(Reg) (B)
(B)
- 2357,532
Eredmények: Lineáris regressziós korrelációs együttható: 0,923
Logaritmikus regressziós korrelációs együttható: 0,998
Logaritmikus regressziós képlet: y = -3857,984 + 2357,532lnx
Becsült értékek számítása
A két változós statisztikai számítással kapott regressziós képlet alapján kiszámítható az y becsült értéke a megadott x-értéknél.
De ki lehet számítani a megfelelő x-értéket is (két értéket, x1 és x2 négyzetes regresszió esetén) a regressziós képletben szereplő y értéknél.
4. példa: Az x becsült értékének kiszámítása, ha a 3. példában szereplő adatok logaritmikus regressziója által meghatározott regressziós képletben y = -130. Adja meg a Fix 3 opciót az eredményhez. (Végezze el az alábbi műveletet, miután végzett a 3. példa műveleteivel.)

 130
130
 (STAT)
(STAT) (Reg)
(Reg) (xˆ)
(xˆ)
- 4,861
Fontos!
A regressziós tényező, korrelációs együttható és becsült érték kiszámítása meglehetősen sokáig eltarthat, ha nagyszámú adattétel fordul elő a számításban.
Normális eloszlással kapcsolatos számítások
Mindaddig, amíg az egy változós statisztikai számítás van kiválasztva, az alább mutatott függvények használatával el tudja végezni a normál eloszlási számítást abból a menüből, amely az alábbi gombművelet elvégzésekor jelenik meg: 
 (STAT)
(STAT) (Distr).
(Distr).
P, Q, R: Ezek a függvények veszik a t argumentumot és meghatározzák a standard normál eloszlás valószínűségét az alább mutatott módon.
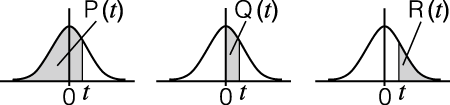
 t: A függvény előtt az X argumentum áll és a normalizált véletlen változót határozza meg X
t: A függvény előtt az X argumentum áll és a normalizált véletlen változót határozza meg X t = X - xσx.
t = X - xσx.
5. példa: Az egy változós adatoknál {xn; freqn} = {0;1, 1;2, 2;1, 3;2, 4;2, 5;2, 6;3, 7;4, 9;2, 10;1} a normalizált véletlen változó meghatározásához ( t) amikor x = 3, és P(t) az illető pontnál, akár három tizedeshelyig (Fix 3).
t) amikor x = 3, és P(t) az illető pontnál, akár három tizedeshelyig (Fix 3).

 (SETUP)
(SETUP)
 (STAT)
(STAT) (ON)
(ON)

 (SETUP)
(SETUP) (Fix)
(Fix)

 (STAT)
(STAT) (1-VAR)
(1-VAR)
- 0
 1
1 2
2 3
3 4
4 5
5 6
6 7
7 9
9 10
10


1 2
2 1
1 2
2 2
2 2
2 3
3 4
4 2
2 1
1
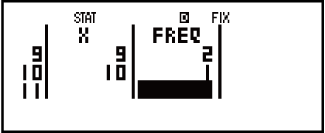
 3
3
 (STAT)
(STAT) (Distr)
(Distr) (
( t)
t)
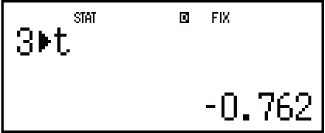

 (STAT)
(STAT) (Distr)
(Distr) (P()
(P()


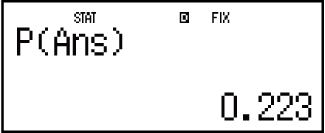
Eredmények: Normalizált véletlen ( t): -0,762
t): -0,762
P(t): 0,223