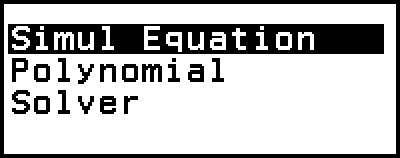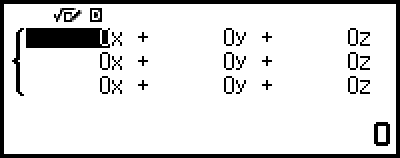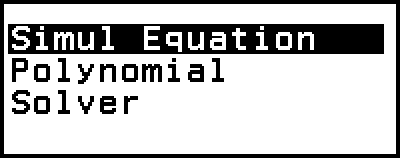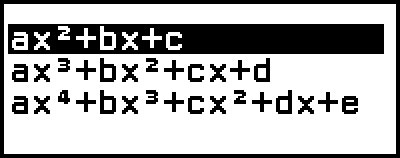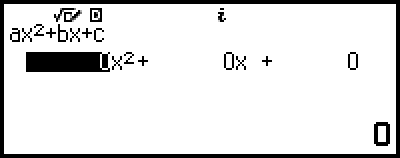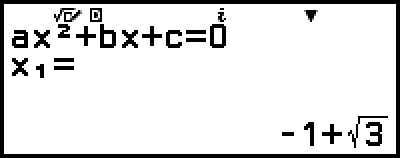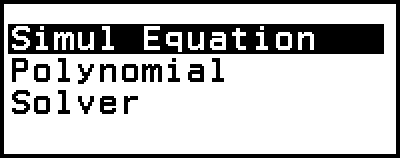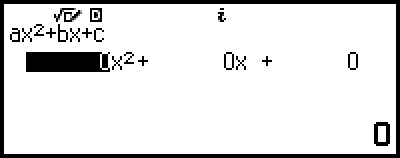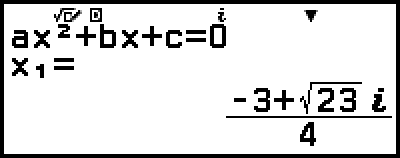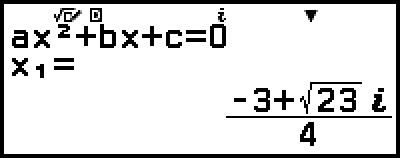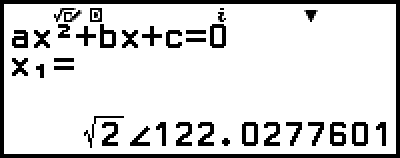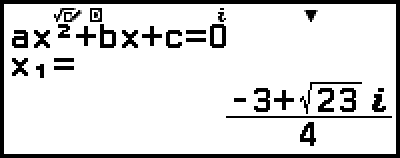Yhtälölaskut
Equation-sovellus sisältää kolme alla kuvattua funktiota. Sovelluksen käynnistämisen jälkeen voit valita haluamasi toiminnon näkyviin tulevasta Equation-valikosta.
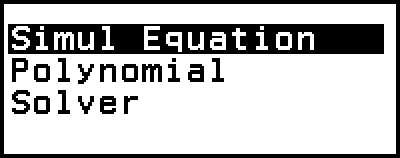
Simul Equation: Lineaarinen yhtälöryhmä, jossa on kaksi, kolme tai neljä tuntematonta
Polynomial: Korkeamman asteen yhtälö toisesta neljänteen asteeseen
Solver: Funktio, joka etsii minkä tahansa syöttöyhtälön sisältämän muuttujan arvon
Lineaarinen yhtälöryhmä
Tässä selitämme yleisen menettelyn yhtälöryhmän ratkaisemiseksi esimerkillä, joka ratkaisee lineaarisen yhtälöryhmän, jossa on kolme tuntematonta.
Esimerkki 1: 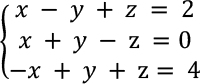
1. Paina  , valitse Equation-sovelluskuvake ja paina sitten
, valitse Equation-sovelluskuvake ja paina sitten  .
.
Tämä tuo näytölle Equation-valikon.
2. Valitse [Simul Equation] ja paina sitten  .
.
Tämä näyttää tuntemattomien valikon määrän.
3. Valitse [3 Unknowns] ja paina sitten  .
.
Tämä tuo näytölle kerroineditorin.
4. Syötä kerroineditoriin kertoimien arvot.
- 1


 ((-))1
((-))1 1
1 2
2
1 1
1

 ((-))1
((-))1 0
0

 ((-))1
((-))1 1
1 1
1 4
4
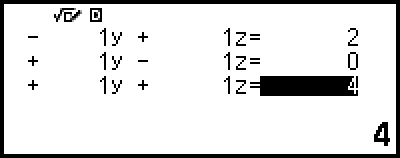
 -näppäimen painaminen kerroineditorin ollessa näytöllä nollaa kaikki kertoimet.
-näppäimen painaminen kerroineditorin ollessa näytöllä nollaa kaikki kertoimet.
5. Paina  .
.
Tämä tuo näytölle ratkaisun.
Kun  -ilmaisin on näytöllä, kaikki
-ilmaisin on näytöllä, kaikki  -näppäimen painallukset (tai
-näppäimen painallukset (tai  ) tuovat näytölle toisen ratkaisun.
) tuovat näytölle toisen ratkaisun.
 (tai
(tai  )
)
 (tai
(tai  )
)
 - tai
- tai  -näppäimen painaminen samalla kun
-näppäimen painaminen samalla kun  -ilmaisin on näytöllä, saa aiemmin näytetyn ratkaisun uudelleen näkyviin.
-ilmaisin on näytöllä, saa aiemmin näytetyn ratkaisun uudelleen näkyviin.
Kun viimeisen ratkaisun jälkeen painetaan  , laskin palaa takaisin kerroineditoriin. Palaa kerroineditoriin minkä tahansa ratkaisun ollessa näytössä painamalla
, laskin palaa takaisin kerroineditoriin. Palaa kerroineditoriin minkä tahansa ratkaisun ollessa näytössä painamalla  .
.
Laskin palauttaa sinut tuntemattomien valikon määrään, kun painat  -näppäintä ja kerroineditori on näkyvissä.
-näppäintä ja kerroineditori on näkyvissä.
Huomaa
Kun kerroineditori on näkyvissä, voit tallentaa korostetun arvon muuttujaan. Ratkaisun ollessa näkyvissä voit myös tallentaa myös sen muuttujaan. Katso lisätietoja muuttujista kohdasta ”Muuttujat (A, B, C, D, E, F, x, y, z)”.
Korkeamman asteen yhtälö toisesta neljänteen asteeseen
Kun ratkaiset korkeamman asteen yhtälön Equation-sovelluksella, alla olevat arvot näytetään yhtälön asteen mukaan.
Toisen asteen yhtälö
Yhtälön ax2+bx+c=0 ratkaisun näyttämisen jälkeen, näytetään minimi- (tai maksimi-) koodinaatit (x, y) yhtälölle y=ax2+bx+c.
Kolmannen asteen yhtälö
Yhtälön ax3+bx2+cx+d=0 ratkaisun näyttämisen jälkeen, näytetään paikallisen minimin (tai paikallisen maksimin) y=ax3+bx2+cx+d koordinaatit (x, y), mutta vain silloin, kun paikallinen minimi tai paikallinen maksimi on olemassa. Jos paikallista minimiä tai maksimiarvoa ei ole, paina  kun viimeinen ratkaisu on näkyvissä, jolloin näyttöön tulee viesti ”No Local Max/Min”.
kun viimeinen ratkaisu on näkyvissä, jolloin näyttöön tulee viesti ”No Local Max/Min”.
Neljännen asteen yhtälö
Yhtälön ax4+bx3+cx2+dx+e=0 ratkaisu näytetään.
Tässä näytämme esimerkin toisen asteen yhtälöstä selittääksemme yleisen menettelyn korkeammat asteen yhtälön ratkaisemiseksi.
Esimerkki 2: x2 + 2x − 2 = 0
(Input/Output: MathI/MathO)
1. Paina  , valitse Equation-sovelluskuvake ja paina sitten
, valitse Equation-sovelluskuvake ja paina sitten  .
.
Tämä tuo näytölle Equation-valikon.
2. Valitse [Polynomial] ja paina sitten  .
.
Tämä näyttää astevalikkojen määrän.
3. Valitse [ax2+bx+c] ja paina sitten  .
.
Tämä tuo näytölle kerroineditorin.
4. Syötä kerroineditoriin kertoimien arvot.
- 1
 2
2

 ((-))2
((-))2
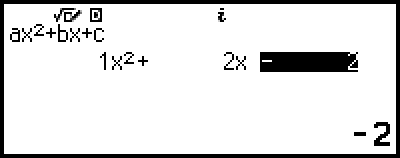
 -näppäimen painaminen kerroineditorin ollessa näytöllä nollaa kaikki kertoimet.
-näppäimen painaminen kerroineditorin ollessa näytöllä nollaa kaikki kertoimet.
5. Paina  .
.
Tämä tuo näytölle ratkaisun.
Kun  -ilmaisin on näkyvissä,
-ilmaisin on näkyvissä,  -näppäimen (tai
-näppäimen (tai  -näppäimen) painaminen tuo näytölle toisen laskentatoimituksen (ratkaisun tai koordinaatin).
-näppäimen) painaminen tuo näytölle toisen laskentatoimituksen (ratkaisun tai koordinaatin).
 (tai
(tai  )
)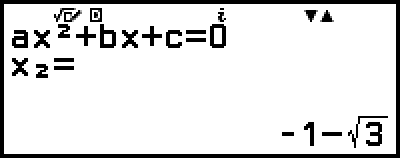
(Näyttää minimin x-koordinaatin arvosta y = x2 + 2x − 2.)
 (tai
(tai  )
)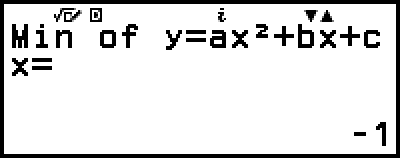
(Näyttää maksimin y-koordinaatin arvosta y = x2 + 2x − 2.)
 (tai
(tai  )
)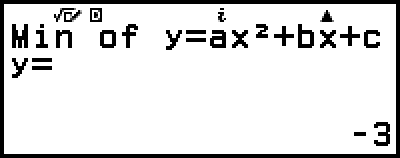
 - tai
- tai  -näppäimen painaminen samalla kun
-näppäimen painaminen samalla kun  -ilmaisin on näytöllä, saa aiemmin näytetyn laskentatulokset uudelleen näkyviin.
-ilmaisin on näytöllä, saa aiemmin näytetyn laskentatulokset uudelleen näkyviin.
Kun viimeisen laskentatuloksen jälkeen painetaan  , laskin palaa takaisin kerroineditoriin. Palaa kerroineditoriin minkä tahansa laskentatuloksen ollessa näytössä painamalla
, laskin palaa takaisin kerroineditoriin. Palaa kerroineditoriin minkä tahansa laskentatuloksen ollessa näytössä painamalla  .
.
Laskin palauttaa sinut astevalikon määrään, kun painat  ja kerroineditori on näkyvissä.
ja kerroineditori on näkyvissä.
Huomaa
Kun kerroineditori on näkyvissä, voit tallentaa korostetun arvon muuttujaan. Kun laskutoimitus (ratkaisu tai koordinaatti) näytetään, se voidaan myös tallentaa muuttujaan. Katso lisätietoja muuttujista kohdasta ”Muuttujat (A, B, C, D, E, F, x, y, z)”.
Kompleksilukuratkaisun näyttö (Complex Roots)
Korkeamman asteen yhtälöillä voi olla kompleksilukuratkaisuja. Kun Polynomial on valittuna Equation-valikossa, voit ottaa kompleksilukuratkaisun näytön käyttöön tai poistaa sen käytöstä alla olevien toimintojen avulla.
 – [Complex Roots] > [On]
– [Complex Roots] > [On] 
Ottaa käyttöön kompleksilukuratkaisun näytön (alkuperäinen oletusasetus).
 – [Complex Roots] > [Off]
– [Complex Roots] > [Off] 
Poistaa käytöstä kompleksilukuratkaisun näytön. Jos syötetään ja suoritetaan yhtälö, jossa on vain yksi tai useampi kompleksilukuratkaisu, näyttöön tulee viesti ”No Real Roots”.
Esimerkki 3: 2x2 + 3x + 4 = 0
(Input/Output: MathI/MathO, Complex Result: a+bi, Complex Roots: On)
1. Paina  , valitse Equation-sovelluskuvake ja paina sitten
, valitse Equation-sovelluskuvake ja paina sitten  .
.
Tämä tuo näytölle Equation-valikon.
2. Valitse [Polynomial] > [ax2+bx+c].
Tämä tuo näytölle kerroineditorin.
3. Syötä kerroineditoriin kertoimien arvot.
- 2
 3
3 4
4

4. Paina  .
.
Tämä tuo näytölle ratkaisun.
5. Näytä toinen ratkaisu ja koordinaattiarvot.
 (tai
(tai  )
)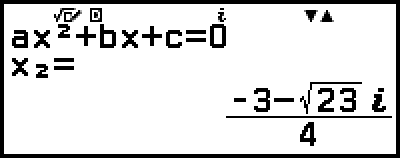
 (tai
(tai  )
)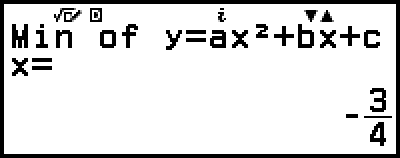
 (tai
(tai  )
)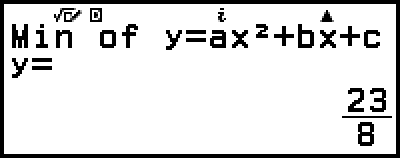
Kun viimeisen laskentatuloksen jälkeen painetaan  , laskin palaa takaisin kerroineditoriin. Palaa kerroineditoriin minkä tahansa laskentatuloksen ollessa näytössä painamalla
, laskin palaa takaisin kerroineditoriin. Palaa kerroineditoriin minkä tahansa laskentatuloksen ollessa näytössä painamalla  .
.
Kompleksilukuratkaisun muuntaminen suorakulmaisiksi koordinaateiksi tai napakoordinaateiksi
Voit muuntaa kompleksilukuratkaisun suorakulmaisten koordinaattien tai napakoordinaattien muotoon käyttämällä FORMAT-valikkoa, joka tulee näkyviin, kun painat  .
.
Esimerkki 4: Muunna esimerkissä 3 näytetty kompleksilukuratkaisu napakoordinaattimuotoon ja sitten suorakulmaisten koordinaattien muotoon
1. Suorita esimerkin 3 vaiheet 1–4.
2. Paina  , valitse [Polar Coord] ja paina sitten
, valitse [Polar Coord] ja paina sitten  .
.
Tämä muuntaa ratkaisun napakoordinaattimuotoon.
3. Paina  , valitse [Rectangular Coord] ja paina sitten
, valitse [Rectangular Coord] ja paina sitten  .
.
Tämä muuntaa ratkaisun suorakulmaisen koordinaatin muotoon.
Solver-sovelluksen käyttö
Solver käyttää Newtonin menetelmää yhtälöiden likiarvon määrittämiseen. Solver tukee seuraavan muotoisten yhtälöiden syöttämistä.
Esimerkkejä: y = x + 5, x = sin(A), xy + C (käsitellään kuin xy + C = 0)
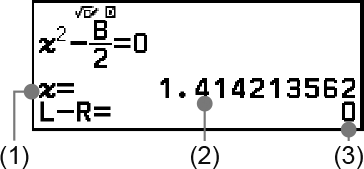
Esimerkki 5: Yhtälön x2 - B2 = 0 ratkaiseminen x:n suhteen, kun B = 4
(Input/Output: MathI/MathO)
Huomaa
Ennen yhtälön x2 - B2 = 0 ratkaisemista x:n suhteen, 4 on tallennettava muuttujaan B. Tämä tehdään alla olevan menettelyn vaiheessa 3.
1. Paina  , valitse Equation-sovelluskuvake ja paina sitten
, valitse Equation-sovelluskuvake ja paina sitten  .
.
Tämä tuo näytölle Equation-valikon.
2. Valitse [Solver] ja paina sitten  .
.
Tämä tuo näytölle Solver-yhtälön syöttöruudun.
3. Tallenna tässä 4 muuttujaan B.

 4
4

Tämä toiminto voidaan suorittaa milloin tahansa ennen tämän menettelyn vaihetta 7.
Katso lisätietoja muuttujista kohdasta ”Muuttujat (A, B, C, D, E, F, x, y, z)”.
Palaa Solver -yhtälön syöttönäyttöön painamalla  .
.
4. Syötä yhtälö.



 (B)
(B) 2
2

 (=)*0
(=)*0
* Voit myös käyttää seuraavaa toimintoa = sign:  – [Equation] > [=] syöttämiseksi.
– [Equation] > [=] syöttämiseksi.
5. Tallenna syöttöyhtälö painamalla  .
.
6. Varmista näkyviin tulevassa Solve Target -näytössä, että [x] on valittuna ja paina sitten  .
.
Tämä tuo esille näytön, jossa on x:n alkuarvo.
7. Syötä x:n alkuarvoksi 1.
- 1


8. Kun olet varmistanut, että [Execute] on valittuna, paina  yhtälön ratkaisemiseksi.
yhtälön ratkaisemiseksi.
(1) Muuttuja ratkaistu
(2) Ratkaisu
(3) (Vasen puoli) – (Oikea puoli) tulos
Ratkaisut esitetään aina desimaalimuodossa.
Mitä lähempänä (Vasen puoli) – (Oikea puoli) -tulos on nollaa, sitä tarkempi ratkaisu on.
9. Paina seuraavaksi näppäintä, joka suorittaa haluamasi toiminnon.
| Toiminto: | Paina tätä näppäintä: |
|---|---|
| Palaa vaiheen 6 näyttöön. |  * * |
| Tallenna syöttölauseke ja palaa vaiheen 4 näyttöön. |  tai tai  |
* Kun painat tätä näppäintä, alkuarvosta tulee viimeksi käyttämäsi alkuarvo laskutoimituksessa.
Tärkeää!
-
Solver iteroi ratkaisua ennalta asetetun määrän kertoja. Jos se ei löydä ratkaisua, se näyttää viereisen näköisen vahvistusnäytön, jossa kysytään, haluatko jatkaa. Jatka painamalla
 , kun [Continue] on valittuna tai peruuta Solver-sovelluksen toiminto valitsemalla [Exit] ja sitten
, kun [Continue] on valittuna tai peruuta Solver-sovelluksen toiminto valitsemalla [Exit] ja sitten  .
. 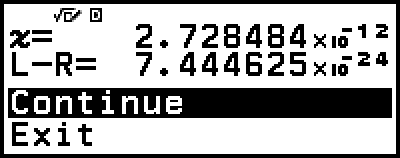
Ratkaisumuuttajalle (x yllä olevassa esimerkissä) syöttämästäsi alkuarvosta riippuen Solver ei välttämättä kykene löytämään ratkaisuja. Jos näin käy, yritä antaa toinen alkuarvo, joka olisi lähempänä ratkaisua.
Solver ei välttämättä pysty määrittämään oikeaa ratkaisua, vaikka sellainen olisi olemassa.
Solver käyttää Newtonin menetelmää, joten silloinkin, kun ratkaisuja on monta, ainoastaan yksi niistä palautetaan.
Newtonin menetelmän rajoitusten vuoksi ratkaisujen löytäminen on usein vaikeaa seuraavan tyyppisille yhtälöille: y=sinx, y=ex, y=√x.