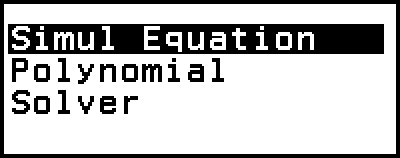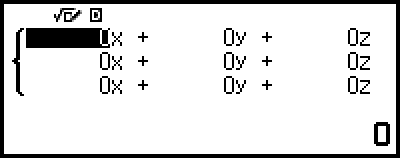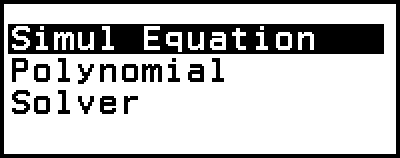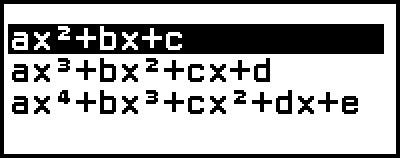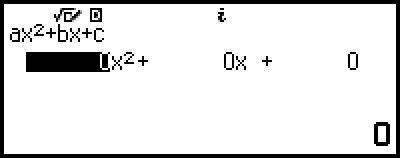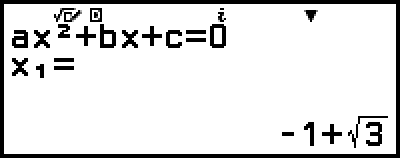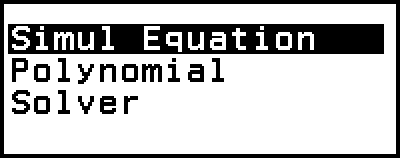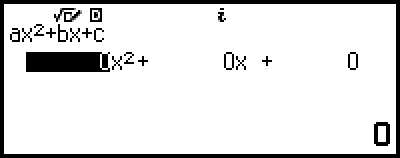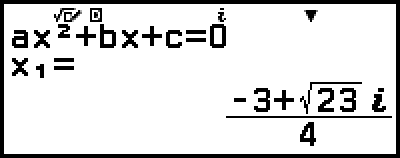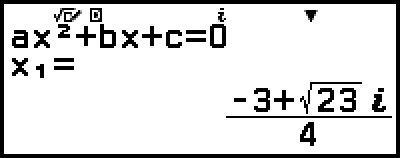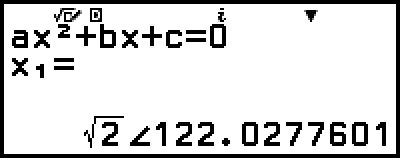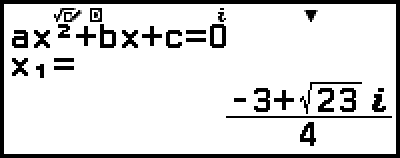Gleichungsberechnungen
Die Equation-Anwendung enthält die drei unten beschriebenen Funktionen. Nach dem Starten der Anwendung können Sie das Menü Equation verwenden, um die gewünschte Funktion auszuwählen.
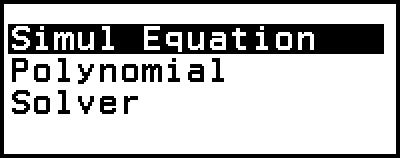
Simul Equation: Simultane lineare Gleichungen mit zwei bis vier Unbekannten
Polynomial: Gleichungen höherer Ordnung 2. bis 4. Grades
Solver: Funktion zur Ermittlung des Wertes einer beliebigen Variablen in einer Eingabegleichung
Simultane lineare Gleichungen
Hier wird das allgemeine Verfahren zur Lösung einer Simultangleichung anhand eines Beispiels erläutert, bei dem eine simultane lineare Gleichungen mit drei Unbekannten gelöst wird.
Beispiel 1: 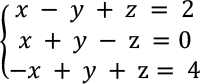
1. Drücken Sie  , wählen Sie das Symbol der Equation-Anwendung und drücken Sie dann
, wählen Sie das Symbol der Equation-Anwendung und drücken Sie dann  .
.
Dadurch wird das Equation-Menü angezeigt.
2. Wählen Sie [Simul Equation] und drücken Sie dann  .
.
Dadurch wird das Menü «Anzahl an Unbekannten» angezeigt.
3. Wählen Sie [3 Unknowns] und drücken Sie dann  .
.
Dadurch wird der Koeffizient-Editor angezeigt.
4. Verwenden Sie den Koeffizient-Editor zur Eingabe von Koeffizientenwerten.
- 1


 ((-))1
((-))1 1
1 2
2
1 1
1

 ((-))1
((-))1 0
0

 ((-))1
((-))1 1
1 1
1 4
4
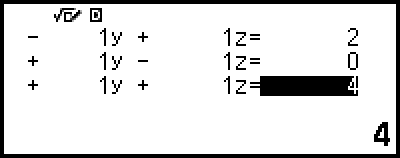
Wenn Sie  drücken, während der Koeffizient-Editor angezeigt wird, werden alle Koeffizienten auf Null gesetzt.
drücken, während der Koeffizient-Editor angezeigt wird, werden alle Koeffizienten auf Null gesetzt.
5. Drücken Sie  .
.
Dadurch wird eine Lösung angezeigt.
Wenn der  -Indikator angezeigt wird, wird durch jedes Drücken von
-Indikator angezeigt wird, wird durch jedes Drücken von  (oder
(oder  ) eine andere Lösung angezeigt.
) eine andere Lösung angezeigt.
 (oder
(oder  )
) 
 (oder
(oder  )
) 
Durch Drücken von  oder
oder  , während der
, während der  -Indikator angezeigt wird, wird die vorherige Lösung angezeigt.
-Indikator angezeigt wird, wird die vorherige Lösung angezeigt.
Durch Drücken von  , während die finale Lösung angezeigt wird, kehren Sie zum Koeffizient-Editor zurück. Um zum Koeffizient-Editor zurückzukehren, während eine Lösung angezeigt wird, drücken Sie
, während die finale Lösung angezeigt wird, kehren Sie zum Koeffizient-Editor zurück. Um zum Koeffizient-Editor zurückzukehren, während eine Lösung angezeigt wird, drücken Sie  .
.
Wenn Sie  drücken, während der Koeffizient-Editor angezeigt wird, kehren Sie zum Menü «Anzahl an Unbekannten» zurück.
drücken, während der Koeffizient-Editor angezeigt wird, kehren Sie zum Menü «Anzahl an Unbekannten» zurück.
Hinweis
Während der Koeffizient-Editor angezeigt wird, können Sie den aktuell markierten Wert in einer Variablen speichern. Während die Lösung angezeigt wird, kann die aktuell angezeigte Lösung auch in einer Variablen gespeichert werden. Für Details zu Variablen siehe «Variablen (A, B, C, D, E, F, x, y, z)».
Gleichungen höherer Ordnung 2. bis 4. Grades
Wenn Sie eine Gleichung höherer Ordnung mit der Equation-Anwendung lösen, werden die folgenden Werte entsprechend dem Grad der Gleichung angezeigt.
Quadratische Gleichung
Nach der Anzeige der Lösung von ax2+bx+c=0 werden die minimalen (oder maximalen) Koordinaten (x, y) für y=ax2+bx+c angezeigt.
Kubische Gleichung
Nach der Anzeige der Lösung von ax3+bx2+cx+d=0 werden die Koordinaten (x, y) des lokalen Minimums (oder lokalen Maximums) von y=ax3+bx2+cx+d nur angezeigt, wenn ein lokales Minimum oder lokales Maximum existiert. Wenn es kein lokales Minimum oder Maximum gibt, erscheint durch Drücken von  die Meldung «No Local Max/Min», während die letzte Lösung angezeigt wird.
die Meldung «No Local Max/Min», während die letzte Lösung angezeigt wird.
Quartische Gleichung
Die Lösung von ax4+bx3+cx2+dx+e=0 wird angezeigt.
Anhand eines Beispiels für eine quadratische Gleichung erläutern wir hier das allgemeine Verfahren zur Lösung einer Gleichung höherer Ordnung.
Beispiel 2: x2 + 2x - 2 = 0
(Input/Output: MathI/MathO)
1. Drücken Sie  , wählen Sie das Symbol der Equation-Anwendung und drücken Sie dann
, wählen Sie das Symbol der Equation-Anwendung und drücken Sie dann  .
.
Dadurch wird das Equation-Menü angezeigt.
2. Wählen Sie [Polynomial] und drücken Sie dann  .
.
Dadurch wird das Menü «Anzahl an Graden» angezeigt.
3. Wählen Sie [ax2+bx+c] und drücken Sie dann  .
.
Dadurch wird der Koeffizient-Editor angezeigt.
4. Verwenden Sie den Koeffizient-Editor zur Eingabe von Koeffizientenwerten.
- 1
 2
2

 ((-))2
((-))2
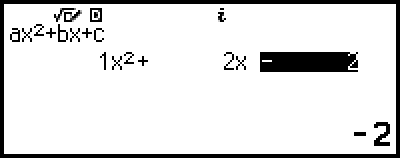
Wenn Sie  drücken, während der Koeffizient-Editor angezeigt wird, werden alle Koeffizienten auf Null gesetzt.
drücken, während der Koeffizient-Editor angezeigt wird, werden alle Koeffizienten auf Null gesetzt.
5. Drücken Sie  .
.
Dadurch wird eine Lösung angezeigt.
Wenn der  -Indikator angezeigt wird, wird durch jedes Drücken von
-Indikator angezeigt wird, wird durch jedes Drücken von  (oder
(oder  ) ein anderes Berechnungsergebnis angezeigt (Lösung oder Koordinate).
) ein anderes Berechnungsergebnis angezeigt (Lösung oder Koordinate).
 (oder
(oder  )
) 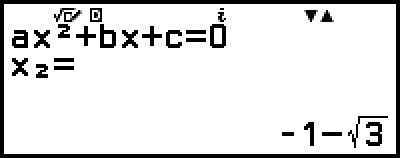
(Zeigt die x-Koordinate des Minimums von y = x2 + 2x - 2 an.)
 (oder
(oder  )
) 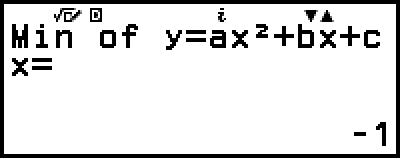
(Zeigt die y-Koordinate des Minimums von y = x2 + 2x - 2 an.)
 (oder
(oder  )
)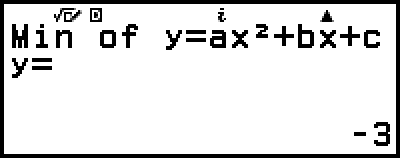
Durch Drücken von  oder
oder  , während der
, während der  -Indikator angezeigt wird, wird das vorherige Berechnungsergebnis erneut angezeigt.
-Indikator angezeigt wird, wird das vorherige Berechnungsergebnis erneut angezeigt.
Durch Drücken von  , während das finale Berechnungsergebnis angezeigt wird, kehren Sie zum Koeffizient-Editor zurück. Um zum Koeffizient-Editor zurückzukehren, während ein Berechnungsergebnis angezeigt wird, drücken Sie
, während das finale Berechnungsergebnis angezeigt wird, kehren Sie zum Koeffizient-Editor zurück. Um zum Koeffizient-Editor zurückzukehren, während ein Berechnungsergebnis angezeigt wird, drücken Sie  .
.
Wenn Sie  drücken, während der Koeffizient-Editor angezeigt wird, kehren Sie zum Menü «Anzahl an Gradmassen» zurück.
drücken, während der Koeffizient-Editor angezeigt wird, kehren Sie zum Menü «Anzahl an Gradmassen» zurück.
Hinweis
Während der Koeffizient-Editor angezeigt wird, können Sie den aktuell markierten Wert in einer Variablen speichern. Auch während ein Berechnungsergebnis (Lösung oder Koordinate) angezeigt wird, kann es in einer Variablen gespeichert werden. Für Details zu Variablen siehe «Variablen (A, B, C, D, E, F, x, y, z)».
Anzeige der Lösung komplexer Zahlen (Complex Roots)
Gleichungen höherer Ordnung können Lösungen mit komplexen Zahlen haben. Wenn im Menü Equation die Option Polynomial ausgewählt ist, können Sie mit den folgenden Operationen die Anzeige der Lösungen für komplexe Zahlen aktivieren oder deaktivieren.
 – [Complex Roots] > [On]
– [Complex Roots] > [On] 
Aktiviert die Anzeige der Lösung für komplexe Zahlen (Vorgabe).
 – [Complex Roots] > [Off]
– [Complex Roots] > [Off] 
Deaktiviert die Anzeige von Lösungen für komplexe Zahlen. Wenn Sie eine Gleichung eingeben und ausführen, die nur eine oder mehrere Lösungen aus komplexen Zahlen hat, erscheint die Meldung «No Real Roots».
Beispiel 3: 2x2 + 3x + 4 = 0
(Input/Output: MathI/MathO, Complex Result: a+bi, Complex Roots: On)
1. Drücken Sie  , wählen Sie das Symbol der Equation-Anwendung und drücken Sie dann
, wählen Sie das Symbol der Equation-Anwendung und drücken Sie dann  .
.
Dadurch wird das Equation-Menü angezeigt.
2. Wählen Sie [Polynomial] > [ax2+bx+c].
Dadurch wird der Koeffizient-Editor angezeigt.
3. Verwenden Sie den Koeffizient-Editor zur Eingabe von Koeffizientenwerten.
- 2
 3
3 4
4

4. Drücken Sie  .
.
Dadurch wird eine Lösung angezeigt.
5. Zeigen Sie eine andere Lösung und Koordinatenwerte an.
 (oder
(oder  )
) 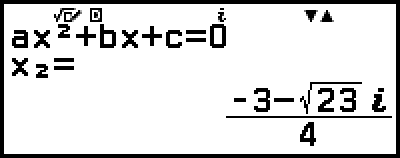
 (oder
(oder  )
) 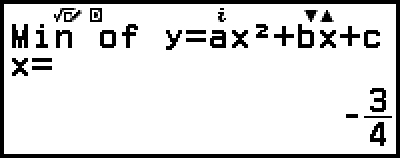
 (oder
(oder  )
)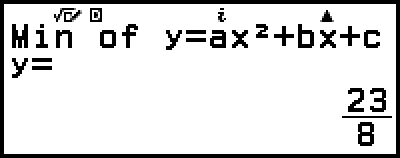
Durch Drücken von  , während das finale Berechnungsergebnis angezeigt wird, kehren Sie zum Koeffizient-Editor zurück. Um zum Koeffizient-Editor zurückzukehren, während ein Berechnungsergebnis angezeigt wird, drücken Sie
, während das finale Berechnungsergebnis angezeigt wird, kehren Sie zum Koeffizient-Editor zurück. Um zum Koeffizient-Editor zurückzukehren, während ein Berechnungsergebnis angezeigt wird, drücken Sie  .
.
Konvertierung einer Lösung von komplexen Zahlenberechnungen in rechtwinklige oder Polarkoordinaten
Sie können mit dem FORMAT-Menü, das erscheint, wenn Sie  drücken, die Lösung einer Berechnung einer komplexen Zahl in das Format von rechtwinkligen oder Polarkoordinaten umwandeln.
drücken, die Lösung einer Berechnung einer komplexen Zahl in das Format von rechtwinkligen oder Polarkoordinaten umwandeln.
Beispiel 4: So konvertieren Sie die in Beispiel 3 dargestellte Lösung mit komplexen Zahlen in das Polarkoordinatenformat und anschliessend in das rechtwinklige Koordinatenformat
1. Führen Sie Schritte 1 bis 4 von Beispiel 3 durch.
2. Drücken Sie  , wählen Sie [Polar Coord] und drücken Sie dann
, wählen Sie [Polar Coord] und drücken Sie dann  .
.
Dadurch wird die Lösung in das Polarkoordinatenformat umgewandelt.
3. Drücken Sie  , wählen Sie [Rectangular Coord] und drücken Sie dann
, wählen Sie [Rectangular Coord] und drücken Sie dann  .
.
Dadurch wird die Lösung in das rechtwinklige Koordinatenformat umgewandelt.
Solver verwenden
Solver verwendet die Newton-Methode, um die Lösung von Gleichungen anzunähern. Solver unterstützt die Eingabe von Gleichungen in den folgenden Formaten.
Beispiele: y = x + 5, x = sin(A), xy + C (wird als xy + C = 0 behandelt)
Beispiel 5: Zur Lösung von x2 - B2 = 0 für x, wenn B = 4
(Input/Output: MathI/MathO)
Hinweis
Vor der Lösung von x2 - B2 = 0 für x muss 4 in Variable B gespeichert werden. Dies wird in Schritt 3 des folgenden Verfahrens ausgeführt.
1. Drücken Sie  , wählen Sie das Symbol der Equation-Anwendung und drücken Sie dann
, wählen Sie das Symbol der Equation-Anwendung und drücken Sie dann  .
.
Dadurch wird das Equation-Menü angezeigt.
2. Wählen Sie [Solver] und drücken Sie dann  .
.
Dadurch wird der Gleichungseingabebildschirm für die Solver angezeigt.
3. Speichern Sie hier 4 in Variable B.
 4
4

Dieser Vorgang kann an jedem beliebigen Punkt vor Schritt 7 dieses Verfahrens durchgeführt werden.
Für Details zu Variablen siehe «Variablen (A, B, C, D, E, F, x, y, z)».
Drücken Sie  , um zum Gleichungseingabebildschirm für Solver zurückzukehren.
, um zum Gleichungseingabebildschirm für Solver zurückzukehren.
4. Geben Sie die Gleichung ein.



 (B)
(B) 2
2

 (=)*0
(=)*0
* Sie können auch die folgende Operation verwenden zur Eingabe von = Vorzeichen:  – [Equation] > [=].
– [Equation] > [=].
5. Drücken Sie  , um die eingegebene Gleichung zu registrieren.
, um die eingegebene Gleichung zu registrieren.
6. Bestätigen Sie auf dem Bildschirm «Solve Target», dass [x] ausgewählt ist und drücken Sie dann  .
.
Dadurch wird ein Bildschirm mit dem Ausgangswert von x angezeigt.
7. Geben Sie 1 als Ausgangswert von x ein.
- 1


8. Nachdem Sie sich vergewissert haben, dass [Execute] ausgewählt ist, drücken Sie  zur Lösung der Gleichung.
zur Lösung der Gleichung.
(1) Variable gelöst für
(2) Lösung
(3) Ergebnis (Linke Seite) − (Rechte Seite)
Lösungen werden immer in Dezimalform dargestellt.
Je näher das Ergebnis (Linke Seite) − (Rechte Seite) an Null ist, desto höher ist die Genauigkeit der Lösung.
9. Drücken Sie als nächstes die Taste, die die gewünschte Operation ausführt.
| Dafür: | Drücken Sie diese Taste: |
|---|---|
| Kehren Sie in Schritt 6 zum Bildschirm zurück. |  * * |
| Speichern Sie den eingegebenen Ausdruck und kehren Sie zum Bildschirm in Schritt 4 zurück. |  oder oder  |
* Wenn Sie diese Taste drücken, wird der Ausgangswert zum Ausgangswert, den Sie zuletzt für die Berechnung verwendet haben.
Wichtig!
-
Solver führt die Konvergenz eine vorgegebene Anzahl von Malen durch. Wenn keine Lösung gefunden wird, erscheint ein Bestätigungsfenster wie das nebenstehende, in dem Sie gefragt werden, ob Sie fortfahren möchten. Drücken Sie
 , während [Continue] ausgewählt ist, um fortzufahren, oder wählen Sie [Exit] und dann
, während [Continue] ausgewählt ist, um fortzufahren, oder wählen Sie [Exit] und dann  , um den Vorgang Solver abzubrechen.
, um den Vorgang Solver abzubrechen. 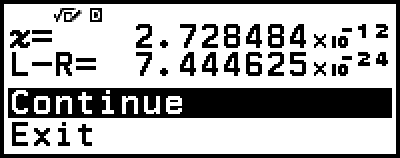
Je nachdem, was Sie als Ausgangswert für die Lösungsvariable (x im obigen Beispiel) eingeben, kann Solver möglicherweise keine Lösung finden. Versuchen Sie in diesem Fall, den Ausgangswert so zu ändern, dass er näher an der Lösung liegt.
Solver kann möglicherweise nicht die korrekte Lösung bestimmen, auch wenn eine existiert.
Solver nutzt die Newton-Methode, wenn es also mehrere Lösungen gibt, wird nur eine von ihnen angezeigt.
Aufgrund der Einschränkungen der Newton-Methode sind Lösungen für Gleichungen wie die folgende nur schwer zu erhalten: y=sinx, y=ex, y=√x.