Dùng SOLVE
SOLVE cho phép bạn giải một biểu thức sử dụng các giá trị biến mà bạn muốn, mà không cần phải chuyển đổi hoặc đơn giản hóa biểu thức đó.
Lưu ý rằng SOLVE được dùng chỉ trong phương thức COMP.
Ví dụ: Để giải y = ax2 + b cho x khi y = 0, a = 1, và b = -2
(Y)
(=)
(A)
(X) 
(B)
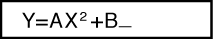
(SOLVE)
- (1) Nhắc nhập giá trị cho Y
(2) Giá trị hiện thời của Y
- 0
- 1
- 2
- (SOLVE)
- Màn hình nghiệm
- Để ra khỏi SOLVE:
Điều quan trọng!
Các hàm sau không được phép đặt trong phương trình: ∫, d/dx, Pol, Rec.
Tuỳ theo những gì bạn nhập cho giá trị khởi đầu (biến nghiệm), SOLVE có thể không có khả năng thu được nghiệm. Nếu điều này xảy ra, hãy thử thay đổi giá trị khởi đầu sao cho gần với nghiệm hơn.
SOLVE có thể không có khả năng xác định nghiệm đúng, ngay cả khi nghiệm tồn tại.
SOLVE dùng phương pháp Newton, vì thế ngay cả khi tồn tại đa nghiệm, máy cũng chỉ trả về một trong số các nghiệm đó.
Do những hạn chế trong phương pháp Newton, nghiệm có xu hướng khó thu được trong những phương trình như sau: y = sin(x), y = ex, y = √x, y = x-1
Nếu một biểu thức không bao gồm dấu bằng (=), SOLVE tạo ra một nghiệm cho biểu thức = 0.
