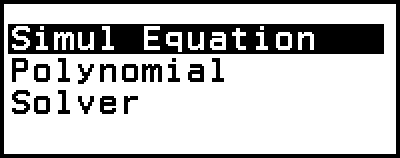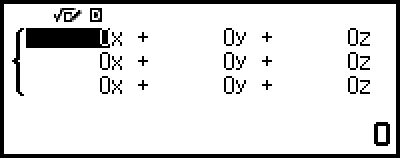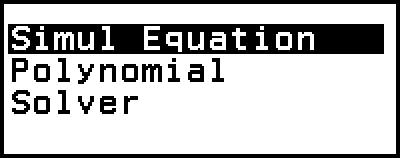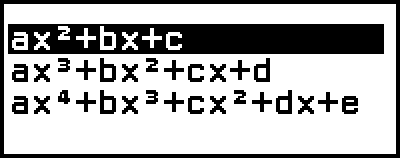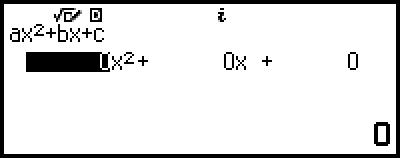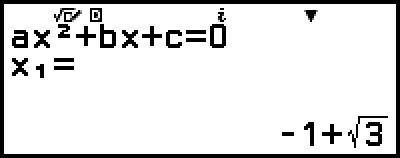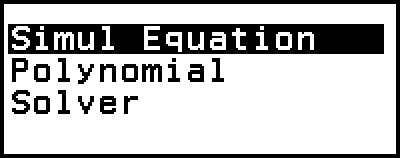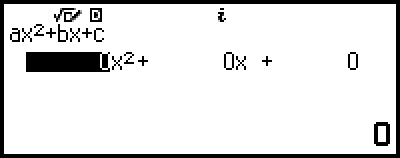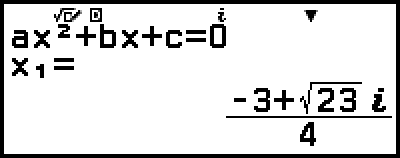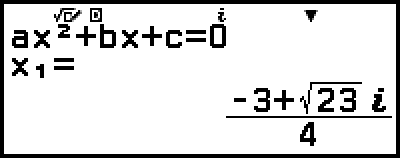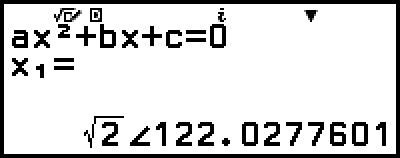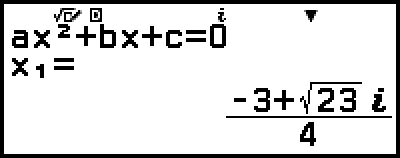Cálculos de ecuaciones
La aplicación Equation incluye las tres funciones que se indican a continuación. Después de iniciar la aplicación, puede utilizar el menú Equation para seleccionar la función que desee.
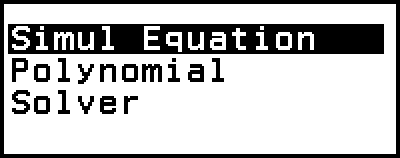
Simul Equation: Sistema de ecuaciones lineales con entre dos y cuatro incógnitas
Polynomial: Ecuaciones de grado superior, de 2º a 4º grado
Solver: Función para encontrar el valor de cualquier variable contenida en una ecuación de entrada
Sistema de ecuaciones lineales
A continuación, se explica el procedimiento general para resolver un sistema de ecuaciones con un ejemplo donde se resuelve un sistema de ecuaciones lineales con tres incógnitas.
Ejemplo 1: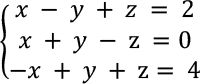 
1. Presione 
, seleccione el ícono de la aplicación Equation y, a continuación, presione 
.
Esto muestra el menú Equation.
2. Seleccione [Simul Equation] y, a continuación, presione .
Esto muestra el menú de número de incógnitas.
3. Seleccione [3 Unknowns] y, a continuación, presione .
Esto muestra el editor de coeficientes.
4. Utilice el editor de coeficientes para introducir valores de coeficientes.
- 1
((-))112
11((-))10
((-))1114 
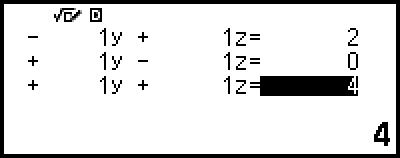
Si presiona 
mientras se muestra el editor de coeficientes, todos los coeficientes se borrarán y equivaldrán a cero.
5. Presione .
Esto mostrará una solución.
Cuando se muestra el indicador 
, cada vez que presione 
(o ) se mostrará otra solución.
- (o )
- (o )
Si presiona 
o 
cuando se muestra el indicador 
, volverá a aparecer la solución mostrada anteriormente.
Presionar mientras se muestra la solución final del cálculo hará que vuelva al editor de coeficientes. Para volver al editor de coeficientes mientras se muestra cualquier resultado de cálculo, presione .
Al presionar mientras se muestra el editor de coeficientes hará que vuelva al menú de número de incógnitas.
Nota
Cuando se muestra el editor de coeficientes, puede almacenar el valor actualmente resaltado en una variable. Asimismo, la solución mostrada actualmente se puede almacenar en una variable. Para obtener más información sobre variables, consulte “Variables (A, B, C, D, E, F, x, y, z)”.
Ecuaciones de grado superior, de 2º a 4º grado
Cuando se resuelve una ecuación de grado superior con la aplicación Equation se muestran los valores indicados a continuación según el grado de la ecuación.
Ecuación cuadrática
Tras la visualización de la solución de ax2+bx+c=0, se muestran las coordenadas (x, y) mínimas (o máximas) de y=ax2+bx+c.
Ecuación cúbica
Tras la visualización de la solución de ax3+bx2+cx+d=0, se muestran las coordenadas (x, y) del mínimo local (o del máximo local) de y=ax3+bx2+cx+d solo si existe un mínimo local o un máximo local. Si no existe un mínimo o un máximo local, al presionar cuando se muestra la última solución aparecerá el mensaje “No Local Max/Min”.
Ecuación cuártica
Se muestra la solución de ax4+bx3+cx2+dx+e=0.
A continuación se muestra un ejemplo de ecuación cuadrática para explicar el procedimiento general de resolución de una ecuación de grado superior.
Ejemplo 2: x2 + 2x − 2 = 0
(Input/Output: MathI/MathO)
1. Presione , seleccione el ícono de la aplicación Equation y, a continuación, presione .
Esto muestra el menú Equation.
2. Seleccione [Polynomial] y, a continuación, presione .
Esto muestra el menú de número de grados.
3. Seleccione [ax2+bx+c] y, a continuación, presione .
Esto muestra el editor de coeficientes.
4. Utilice el editor de coeficientes para introducir valores de coeficientes.
- 12((-))2
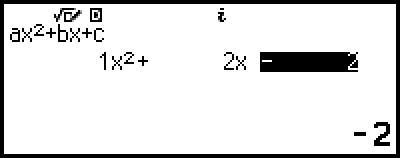
Si presiona mientras se muestra el editor de coeficientes, todos los coeficientes se borrarán y equivaldrán a cero.
5. Presione .
Esto mostrará una solución.
Cuando se muestra el indicador , cada vez que presione (o ) se mostrará resultado del cálculo (solución o coordenada).
- (o )
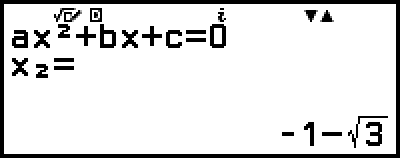
(Muestra la coordenada x del mínimo de y = x2 + 2x − 2.)
- (o )
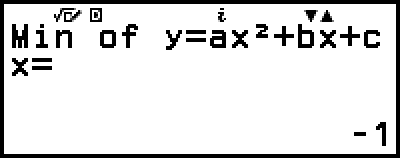
(Muestra la coordenada y del mínimo de y = x2 + 2x − 2.)
- (o )
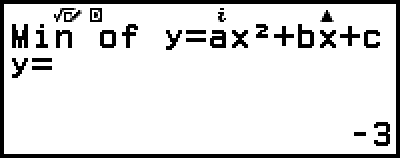
Si presiona o cuando se muestra el indicador , volverá a aparecer el resultado de cálculo mostrado anteriormente.
Al presionar mientras se muestra el resultado final del cálculo, volverá al editor de coeficientes. Para volver al editor de coeficientes mientras se muestra cualquier resultado de cálculo, presione .
Al presionar mientras se muestra el editor de coeficientes hará que vuelva al menú de número de grados.
Nota
Cuando se muestra el editor de coeficientes, puede almacenar el valor actualmente resaltado en una variable. Asimismo, cuando se muestra el resultado de un cálculo (solución o coordenada), dicho resultado se puede almacenar en una variable. Para obtener más información sobre variables, consulte “Variables (A, B, C, D, E, F, x, y, z)”.
Visualización de soluciones de números complejos (Complex Roots)
Las ecuaciones de grado superior pueden tener soluciones de números complejos. Cuando se selecciona Polynomial en el menú Equation, se pueden utilizar las operaciones a continuación para activar o desactivar la visualización de soluciones de números complejos.
– [Complex Roots] > [On]
Activa la visualización de la solución de números complejos (ajuste inicial por defecto).
– [Complex Roots] > [Off]
Desactiva la visualización de la solución de números complejos. Si se introduce y ejecuta una ecuación que solo tiene una o más soluciones de números complejos, aparecerá el mensaje “No Real Roots”.
Ejemplo 3: 2x2 + 3x + 4 = 0
(Input/Output: MathI/MathO, Complex Result: a+bi, Complex Roots: On)
1. Presione , seleccione el ícono de la aplicación Equation y, a continuación, presione .
Esto muestra el menú Equation.
2. Seleccione [Polynomial] > [ax2+bx+c].
Esto muestra el editor de coeficientes.
3. Utilice el editor de coeficientes para introducir valores de coeficientes.
- 234
4. Presione .
Esto mostrará una solución.
5. Mostrar otra solución y valores de coordenadas.
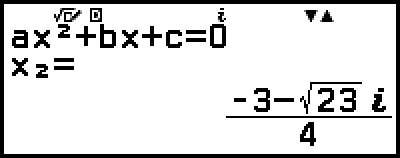
- (o )
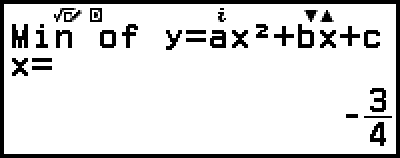
- (o )
- (o )
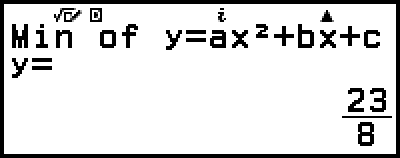
Al presionar mientras se muestra el resultado final del cálculo, volverá al editor de coeficientes. Para volver al editor de coeficientes mientras se muestra cualquier resultado de cálculo, presione .
Convertir una solución de número complejo en coordenadas rectangulares o polares
Puede utilizar el menú FORMAT que aparece al presionar 
para convertir una solución de cálculo de números complejos en formato de coordenadas rectangulares o polares.
Ejemplo 4: Para convertir la solución de números complejos mostrada en el Ejemplo 3 a formato de coordenadas polares y, seguidamente, a formato de coordenadas rectangulares
1. Siga los pasos 1 a 4 del Ejemplo 3.
2. Presione , seleccione [Polar Coord] y, a continuación, presione .
Así se convierte la solución al formato de coordenadas polares.
3. Presione , seleccione [Rectangular Coord] y, a continuación, presione .
Así se convierte la solución al formato de coordenadas rectangulares.
Uso de Solver
Solver utiliza el método de Newton para aproximar la solución de las ecuaciones. Solver admite la entrada de ecuaciones de los formatos que se indican a continuación.
Ejemplos: y = x + 5, x = sin(A), xy + C (tratado como xy + C = 0)
Ejemplo 5: Resolver x2 - B2 = 0 para x cuando B = 4
(Input/Output: MathI/MathO)
Nota
Antes de resolver x2 - B2 = 0 para x, se necesita almacenar 4 en la variable B. Esto se realiza en el paso 3 del procedimiento a continuación.
1. Presione , seleccione el ícono de la aplicación Equation y, a continuación, presione .
Esto muestra el menú Equation.
2. Seleccione [Solver] y, a continuación, presione .
Así se muestra la pantalla de introducción de Solver.
3. Almacene 4 en la variable B aquí.
4
Esta operación puede ejecutarse en cualquier momento previo al paso 7 de este procedimiento.
Para obtener más información sobre variables, consulte “Variables (A, B, C, D, E, F, x, y, z)”.
Presione para volver a la pantalla de introducción de ecuaciones Solver.
4. Introduzca la ecuación.
(B)
2
(=)*0
* También puede utilizar la operación que se indica a continuación para introducir =: 
– [Equation] > [=].
5. Presione para registrar la ecuación introducida.
6. En la pantalla Solve Target, confirme que está seleccionada [x] y, a continuación, presione .
Esto muestra una pantalla con el valor inicial de x.
7. Introduzca 1 como valor inicial de x.
- 1
8. Tras asegurarse de que [Execute] está seleccionado, presione para resolver la ecuación.
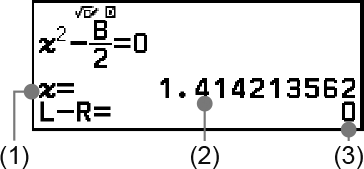
(1) Variable resuelta
(2) Solución
(3) Resultado (lado izquierdo) − (lado derecho)
Las soluciones se muestran siempre en forma decimal.
Cuanto más se acerque el resultado (lado izquierdo) − (lado derecho) a cero, mayor será la precisión de la solución.
9. A continuación, presione la tecla que realiza la operación que desea.
| Para ello: | Presione esta tecla: |
|---|---|
| Vuelve a la pantalla del paso 6. | * |
| Almacena la expresión introducida y vuelve a la pantalla del paso 4. | o |
* El valor inicial al presionar esta tecla se convierte en el último valor inicial utilizado para el cálculo.
¡Importante!
-
Solver realiza la convergencia un número preestablecido de veces. Si no puede encontrar una solución, aparecerá una pantalla de confirmación, parecida a la cercana, preguntando si desea continuar. Presione
mientras selecciona [Continue] para continuar o seleccione [Exit] y, a continuación, para cancelar la operación de Solver.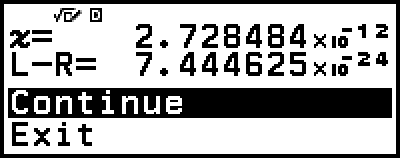 
Dependiendo de lo que haya introducido para el valor inicial de la variable de solución (x en el ejemplo anterior), es posible que Solver no pueda obtener una solución. Si esto ocurre, intente cambiar el valor inicial para que se acerque más a la solución.
Es posible que Solver no pueda determinar la solución correcta aunque dicha solución exista.
Solver utiliza el método de Newton, por lo que, aunque haya varias soluciones, solo se devolverá una de ellas.
Debido a las limitaciones del método de Newton, las soluciones suelen ser difíciles de obtener para ecuaciones como las siguientes: y=sinx, y=ex, y=√x.
