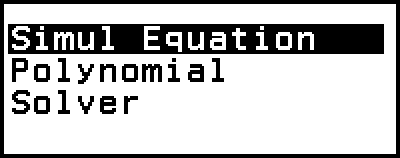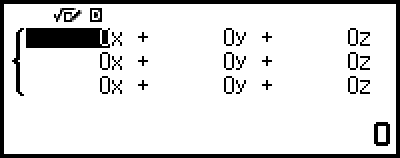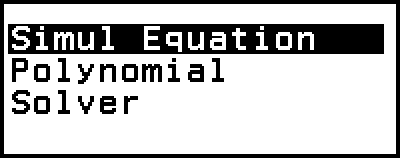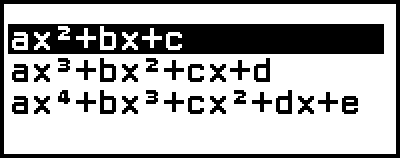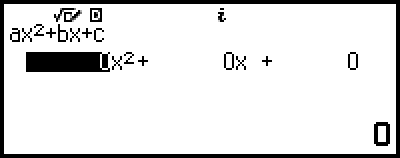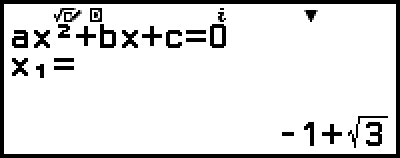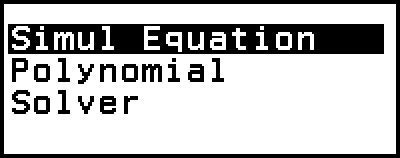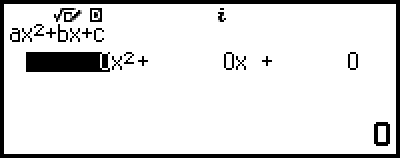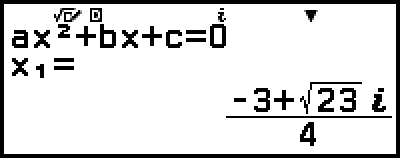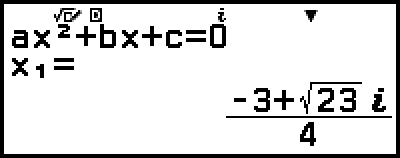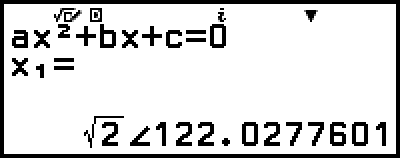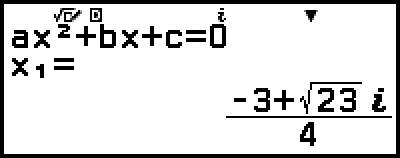方程式計算
Equation 應用程式包含下述三種函數。啟動應用程式後,可使用顯示的 Equation 選單,選擇您要的函數。
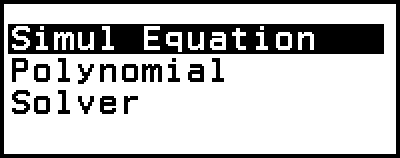
Simul Equation:帶有兩至四個未知數的聯立一次方程式
Polynomial:二次至四次的高次方程式
Solver:用於尋找輸入方程式中,包含之任何變數值的函數
聯立一次方程式
此處以帶有三個未知數的聯立一次方程式為例,說明解聯立一次方程式的一般程序。
範例 1: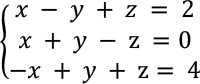
1.按下  ,選擇 Equation 應用程式圖示,然後按下
,選擇 Equation 應用程式圖示,然後按下  。
。
這會顯示 Equation 選單。
2.選擇 [Simul Equation],然後按下  。
。
這會顯示未知數數量選單。
3.選擇 [3 Unknowns],然後按下  。
。
這會顯示係數編輯畫面。
4.使用係數編輯畫面輸入係數值。
- 1


 ((-))1
((-))1 1
1 2
2
1 1
1

 ((-))1
((-))1 0
0

 ((-))1
((-))1 1
1 1
1 4
4
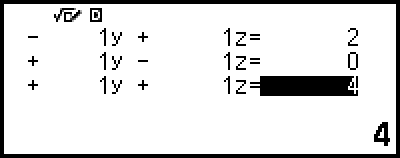
在顯示係數編輯畫面時按下  ,將清除所有係數,使之為零。
,將清除所有係數,使之為零。
5.按  鍵。
鍵。
此時將會顯示解的內容。
當顯示  指示符號時,每次按下
指示符號時,每次按下  (或
(或  )都會顯示另一個解。
)都會顯示另一個解。
 (或
(或  )
)
 (或
(或  )
)
在  指示符號顯示時按下
指示符號顯示時按下  或
或  ,會重新顯示先前顯示的解。
,會重新顯示先前顯示的解。
在顯示最後一個解之後,按下  鍵會返回係數編輯畫面。在顯示了任意一個解之後,如果您想要返回係數編輯畫面,請按下
鍵會返回係數編輯畫面。在顯示了任意一個解之後,如果您想要返回係數編輯畫面,請按下  鍵。
鍵。
在顯示係數編輯畫面時按下  ,會返回未知數數量選單。
,會返回未知數數量選單。
注意
當係數編輯畫面顯示時,可將目前反白顯示的值儲存至變數。此外,當解正在顯示時,目前顯示的解可儲存至變數。如需變數的詳細資訊,請參閱「變數(A、B、C、D、E、F、x、y、z)」。
二次至四次的高次方程式
當您使用 Equation 應用程式解高次方程式時,以下數值會根據方程式的次數顯示。
二次方程式
在顯示 ax2+bx+c=0 的解後,會顯示 y=ax2+bx+c 的最小值(或最大值)座標(x、y)。
三次方程式
在顯示 ax3+bx2+cx+d=0 的解後,僅在存在局部最小值或局部最大值時,會顯示 y=ax3+bx2+cx+d 的局部最小值(或局部最大值)座標(x、y)。如果不存在局部最小值或局部最大值,則在最後解顯示時按下  ,將會顯示「No Local Max/Min」訊息。
,將會顯示「No Local Max/Min」訊息。
四次方程式
ax4+bx3+cx2+dx+e=0 的解會顯示。
此處以二次方程式為例,說明解高次方程式的一般程序。
範例 2:x2 + 2x − 2 = 0
(Input/Output:MathI/MathO)
1.按下  ,選擇 Equation 應用程式圖示,然後按下
,選擇 Equation 應用程式圖示,然後按下  。
。
這會顯示 Equation 選單。
2.選擇 [Polynomial],然後按下  。
。
這會顯示次數選單。
3.選擇 [ax2+bx+c],然後按下  。
。
這會顯示係數編輯畫面。
4.使用係數編輯畫面輸入係數值。
- 1
 2
2

 ((-))2
((-))2
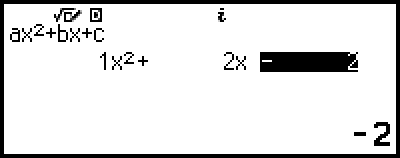
在顯示係數編輯畫面時按下  ,將清除所有係數,使之為零。
,將清除所有係數,使之為零。
5.按  鍵。
鍵。
此時將會顯示解的內容。
當顯示  指示符號時,每次按下
指示符號時,每次按下  (或
(或  ),都會顯示另一個計算結果(解或座標)。
),都會顯示另一個計算結果(解或座標)。
 (或
(或  )
)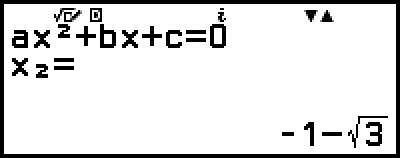
(顯示 y = x2 + 2x − 2 的最小值 x 座標。)
 (或
(或  )
)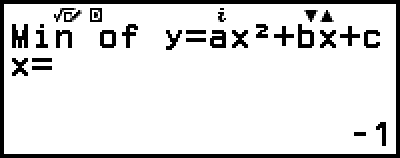
(顯示 y = x2 + 2x − 2 的最小值 y 座標。)
 (或
(或  )
)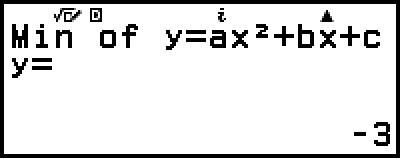
在  指示符號顯示時按下
指示符號顯示時按下  或
或  ,會重新顯示先前顯示的計算結果。
,會重新顯示先前顯示的計算結果。
在顯示了最後計算結果之後,按下  鍵會返回係數編輯畫面。在顯示了任意一個計算結果之後,如果您想要返回係數編輯畫面,請按下
鍵會返回係數編輯畫面。在顯示了任意一個計算結果之後,如果您想要返回係數編輯畫面,請按下  鍵。
鍵。
在顯示係數編輯畫面時按下  ,會返回次數選單。
,會返回次數選單。
注意
當係數編輯畫面顯示時,可將目前反白顯示的值儲存至變數。此外,當顯示計算結果(解或座標)時,可將其儲存至變數。如需變數的詳細資訊,請參閱「變數(A、B、C、D、E、F、x、y、z)」。
複數解顯示(Complex Roots)
高次方程式可能有複數解。當在 Equation 選單上選擇 Polynomial 時,可使用下列操作啟用或停用複數解顯示。
 – [Complex Roots] > [On]
– [Complex Roots] > [On] 
啟用複數解顯示(初始預設值)。
 – [Complex Roots] > [Off]
– [Complex Roots] > [Off] 
停用複數解顯示。輸入並執行僅具有一或多個複數解的方程式,將會顯示「No Real Roots」訊息。
範例 3:2x2 + 3x + 4 = 0
(Input/Output:MathI/MathO,Complex Result:a+bi,Complex Roots:On)
1.按下  ,選擇 Equation 應用程式圖示,然後按下
,選擇 Equation 應用程式圖示,然後按下  。
。
這會顯示 Equation 選單。
2.選擇 [Polynomial] > [ax2+bx+c]。
這會顯示係數編輯畫面。
3.使用係數編輯畫面輸入係數值。
- 2
 3
3 4
4

4.按  鍵。
鍵。
此時將會顯示解的內容。
5.顯示其他解及座標值。
 (或
(或  )
)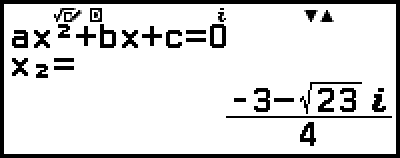
 (或
(或  )
)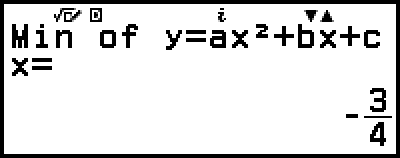
 (或
(或  )
)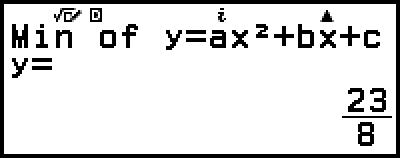
在顯示了最後計算結果之後,按下  鍵會返回係數編輯畫面。在顯示了任意一個計算結果之後,如果您想要返回係數編輯畫面,請按下
鍵會返回係數編輯畫面。在顯示了任意一個計算結果之後,如果您想要返回係數編輯畫面,請按下  鍵。
鍵。
將複數解轉換為直角或極座標
您可使用按下  時顯示的 FORMAT 選單,將複數解轉換為直角座標或極座標格式。
時顯示的 FORMAT 選單,將複數解轉換為直角座標或極座標格式。
範例 4:若要將範例 3 中顯示的複數解轉換為極座標格式,接著再轉換為直角座標格式
1.執行範例 3 的步驟 1 至 4。
2.按下  ,選擇 [Polar Coord],然後按下
,選擇 [Polar Coord],然後按下  。
。
這會將解轉換為極座標格式。
3.按下  ,選擇 [Rectangular Coord],然後按下
,選擇 [Rectangular Coord],然後按下  。
。
這會將解轉換為直角座標格式。
使用 Solver
Solver 使用牛頓近似法解方程式。Solver 支援輸入下列格式的方程式。
範例:y = x + 5,x = sin(A),xy + C(視為 xy + C = 0)
範例 5:若要在 B = 4 時解出 x2 - B2 = 0 的 x
(Input/Output:MathI/MathO)
注意
在解出 x2 - B2 = 0 的 x 之前,4 必須儲存至變數 B。這會在下列程序的步驟 3 完成。
1.按下  ,選擇 Equation 應用程式圖示,然後按下
,選擇 Equation 應用程式圖示,然後按下  。
。
這會顯示 Equation 選單。
2.選擇 [Solver],然後按下  。
。
這會顯示 Solver 方程式輸入畫面。
3.在此將 4 儲存至變數 B。
4.輸入方程式。

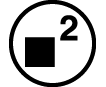


 (B)
(B) 2
2

 (=)*0
(=)*0
* 您也可使用下列操作輸入 = 符號: – [Equation] > [=]。
– [Equation] > [=]。
5.按下  登錄輸入方程式。
登錄輸入方程式。
6.在顯示的 Solve Target 畫面上,確認已選擇 [x] 並按下  。
。
這會顯示含有 x 初始值的畫面。
7.輸入 1 作為 x 的初始值。
- 1


8.確認已選擇 [Execute] 後,按下  解方程式。
解方程式。
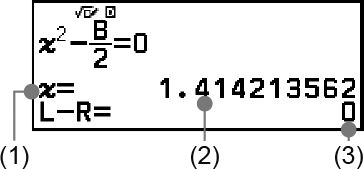
(1) 求解
(2) 解法
(3) (左側) − (右側) 形成結果
解答永遠會以小數形式顯示。
(左側) − (右側) 結果越接近零,解答的準確性較高。
9.接著,按下您要執行之操作的按鍵。
| 執行的操作: | 按下本鍵: |
|---|---|
| 返回步驟 6 中的畫面。 |  * * |
| 儲存輸入表示式並返回步驟 4 中的畫面。 |  或 或  |
* 您按下此鍵時的初始值,會變為上次用於計算的初始值。
重要!
-
Solver 會執行預設的收斂次數。如果無法找到解,則會顯示如一旁所示的確認畫面,詢問您是否繼續。在選擇 [Continue] 時按下
 可繼續,或選擇 [Exit] 並按下
可繼續,或選擇 [Exit] 並按下  ,以取消 Solver 操作。
,以取消 Solver 操作。 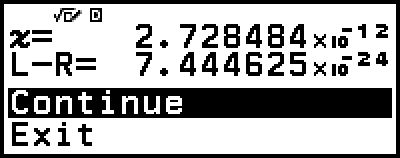
根據您為求解變數(上述範例中的 x)輸入的初始值,Solver 可能無法求得解。如果發生這種情形,請試著改變初始值,使其更接近解答。
Solver 可能無法判斷正確的解,即使該解存在。
Solver 使用牛頓法,所以即使有多個解,也只會傳回一個解。
由於受到牛頓法則的限制,使得難以求得如下列各方程式的解答:y=sinx,y=ex,y=√x。