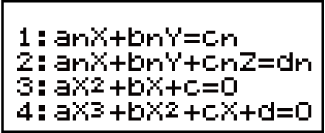fx-570ES PLUS
fx-991ES PLUS
(2nd edition / NATURAL-V.P.A.M.)
Hesap Makinesini Kullanmadan Önce
Hesaplama Modları ve Hesap Makinesi Ayarları
İfadeler ve Değerler Girme
- ▶Temel Giriş Kuralları
- ▶Natural Display ile Giriş Yapma
- ▶√ Hesaplama Aralığını Oluşturma
- ▶Değerleri ve İfadeleri Bağımsız Değişken Olarak Kullanma (Yalnızca Natural Display ile)
- ▶Giriş Modunun Üzerine Yazma (Yalnızca Linear Display için)
- ▶İfadeyi Düzeltme ve Silme
Temel Hesaplamalar
- ▶Hesaplama Sonuçları Arasında Geçiş Yapma
- ▶Kesirli Hesaplamalar
- ▶Yüzde Hesaplamaları
- ▶Derece, Dakika, Saniye (Altmışlı Kesir) Hesaplamaları
- ▶Çoklu İfadeler
- ▶Mühendislik Gösterimi Kullanma
- ▶Hesaplama Geçmişi ve Tekrar Görüntüleme
- ▶Bellek İşlevlerini Kullanma
Fonksiyon Hesaplamaları
- ▶Pi (π), Doğal logaritma tabanı e
- ▶Trigonometrik Fonksiyonlar
- ▶Hiperbolik Fonksiyonlar
- ▶Açı Birimini Dönüştürme
- ▶Üstel Fonksiyonlar
- ▶Logaritmik Fonksiyon
- ▶Güç Fonksiyonları ve Güç Kök Fonksiyonları
- ▶İntegral Hesaplamaları
- ▶Diferansiyel Hesaplamaları
- ▶Σ Hesaplamaları
- ▶Dik-Kutupsal Koordinat Dönüştürme
- ▶Faktöriyel Fonksiyon (!)
- ▶Mutlak Değer Fonksiyonu (Abs)
- ▶Rasgele Sayı (Ran#)
- ▶Rasgele Tamsayı (RanInt#)
- ▶Permütasyon (nPr) ve Kombinasyon (nCr)
- ▶Yuvarlama Fonksiyonu (Rnd)
- ▶CALC Kullanma
- ▶SOLVE Kullanma
- ▶Bilimsel Sabitler
- ▶Metrik Dönüştürme
Hesaplama Modlarını Kullanma
- ▶Karmaşık Sayı Hesaplamaları (CMPLX)
- ▶İstatistik Hesaplamaları (STAT)
- ▶n Tabanı Hesaplamaları (BASE-N)
- ▶Denklem Hesaplamaları (EQN)
- ▶Matris hesaplamaları (MATRIX)
- ▶Bir Fonksiyondan Sayısal Tablo Oluşturma (TABLE)
- ▶Vektör Hesaplamaları (VECTOR)
Teknik Bilgiler
- ▶Hatalar
- ▶Hesap Makinesinin Arızalandığı Sonucuna Varmadan Önce...
- ▶Pili Değiştirme
- ▶Hesaplamada Öncelik Sırası
- ▶Hesaplama Aralıkları, Basamak Sayısı ve Kesinlik
- ▶Teknik Özellikler
- ▶Hesap Makinenizin Gerçekliğini Doğrulama
Sık Sorulan Sorular
Denklem Hesaplamaları (EQN)
İki veya üç bilinmeyenli eş zamanlı doğrusal denklemleri, ikinci dereceden denklemleri ve üçüncü dereceden denklemleri çözmek için EQN Mode'da aşağıdaki yordamı kullanabilirsiniz.
1. 
 (EQN) tuşuna basarak EQN Mode'a geçin.
(EQN) tuşuna basarak EQN Mode'a geçin.
2. Görüntülenen menüden bir denklem türü seçin.
| Bu hesaplama türünü seçmek için: | Şu tuşa basın: |
|---|---|
| İki bilinmeyenli eş zamanlı doğrusal denklemler |  (anX + bnY = cn) (anX + bnY = cn) |
| Üç bilinmeyenli eş zamanlı doğrusal denklemler |  (anX + bnY + cnZ = dn) (anX + bnY + cnZ = dn) |
| İkinci dereceden denklemler |  (aX2 + bX + c = 0) (aX2 + bX + c = 0) |
| Üçüncü dereceden denklemler |  (aX3 + bX2 + cX + d = 0) (aX3 + bX2 + cX + d = 0) |
3. Görüntülenen Coefficient Editor'ı kullanarak, katsayı değerlerini girin.
Örneğin, 2x2 + x - 3 = 0 denklemini çözmek için, 2 adımda  tuşuna basın ve katsayılar için şunları girin: (a = 2, b = 1, c = -3): 2
tuşuna basın ve katsayılar için şunları girin: (a = 2, b = 1, c = -3): 2 1
1
 3
3 .
.
Girdiğiniz bir katsayı değerini değiştirmek için, işaretçiyi uygun hücreye getirip yeni değeri girin ve  tuşuna basın.
tuşuna basın.
 tuşuna basmak, tüm katsayıları sıfır olarak ayarlar.
tuşuna basmak, tüm katsayıları sıfır olarak ayarlar.
Önemli!
Coefficient Editor şu işlemleri desteklemez:  ,
, 
 (M-),
(M-), 
 (STO). Pol, Rec ve çoklu ifadeler de Coefficient Editor ile girilemez.
(STO). Pol, Rec ve çoklu ifadeler de Coefficient Editor ile girilemez.
4. Tüm değerleri istediğiniz şekilde girdikten sonra  tuşuna basın.
tuşuna basın.
Bu işlem bir sonuç görüntüler.  tuşuna her bastığınızda başka bir çözüm görüntülenir. Son çözüm görüntülenirken
tuşuna her bastığınızda başka bir çözüm görüntülenir. Son çözüm görüntülenirken  tuşuna basmak, Coefficient Editor'a döndürür.
tuşuna basmak, Coefficient Editor'a döndürür.
 ve
ve  tuşlarını kullanarak çözümler arasında gezinebilirsiniz.
tuşlarını kullanarak çözümler arasında gezinebilirsiniz.
Herhangi bir çözüm görüntülenirken Coefficient Editor'a dönmek için  tuşuna basın.
tuşuna basın.
Not
Natural Display seçili olsa da, eş zamanlı doğrusal denklemlerin çözümleri √ içerecek bir biçimde görüntülenmez.
Çözüm ekranındaki değerler mühendislik gösterimine dönüştüremez.
Geçerli Denklem Türü Ayarını Değiştirme

 (EQN) tuşuna basın ve görüntülenen menüden bir denklem türü seçin. Denklem türünü değiştirmek, tüm Coefficient Editor katsayılarının sıfıra döndürülmesine neden olur.
(EQN) tuşuna basın ve görüntülenen menüden bir denklem türü seçin. Denklem türünü değiştirmek, tüm Coefficient Editor katsayılarının sıfıra döndürülmesine neden olur.
EQN Mode ile Hesaplama Örnekleri
Örnek 1: x + 2y = 3, 2x + 3y = 4

 (EQN)
(EQN) (anX + bnY = cn)
(anX + bnY = cn)
1 2
2 3
3
2 3
3 4
4
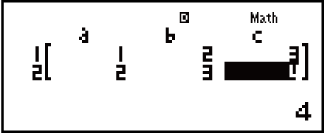

- (X=) -1

- (Y=) 2
Örnek 2: x - y + z = 2, x + y - z = 0, -x + y + z = 4

 (EQN)
(EQN) (anX + bnY + cnZ = dn)
(anX + bnY + cnZ = dn)
1
 1
1 1
1 2
2
1 1
1
 1
1 0
0
 1
1 1
1 1
1 4
4
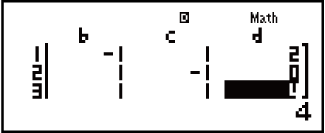

- (X=) 1

- (Y=) 2

- (Z=) 3
Örnek 3: x2 + x + 34 = 0 (MthIO-MathO)

 (EQN)
(EQN) (aX2 + bX + c = 0)
(aX2 + bX + c = 0)
1 1
1 3
3 4
4

- (X1=) - 12 + √22i

- (X2=) - 12 - √22i
Örnek 4: x2 - 2√2x + 2 = 0 (MthIO-MathO)

 (EQN)
(EQN) (aX2 + bX + c = 0)
(aX2 + bX + c = 0)
1
 2
2 2
2
 2
2

- (X=) √2
Örnek 5: x3 - 2x2 - x + 2 = 0

 (EQN)
(EQN) (aX3 + bX2 + cX + d = 0)
(aX3 + bX2 + cX + d = 0)
1
 2
2
 1
1 2
2

- (X1=) -1

- (X2=) 2

- (X3=) 1