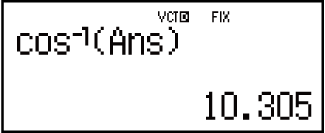Векторные вычисления (VECTOR)

Используйте режим VECTOR для выполнения вычислений двумерных и трехмерных векторов. Для выполнения векторных вычислений необходимо сначала присвоить данные специальным векторным переменным (VctA, VctB, VctC), а затем использовать переменные в вычислении, как показано в примере ниже.

Пример 1. Присвоение (1, 2) переменной VctA и (3, 4) переменной VctB, а также выполнение следующих расчетов: (1, 2) + (3, 4)

1. Нажмите клавиши (VECTOR) для входа в режим VECTOR.

2. Нажмите (VctA)(2).

В результате откроется редактор векторов, позволяющий ввести двумерный вектор для переменной VctA.

(1) «A» обозначает «VctA».

3. Введите элементы VctA: 12.

4. Нажмите следующие клавиши:
(VECTOR)(Data)(VctB)(2).

В результате откроется редактор векторов, позволяющий ввести двумерный вектор для переменной VctB.

5. Введите элементы для VctB: 34.

6. Нажмите для перехода на экран вычислений и выполнения вычисления (VctA+VctB):
(VECTOR)(VctA)(VECTOR)(VctB).

При этом отображается экран VctAns, содержащий результаты вычислений.

(2) «Ans» обозначает «VctAns».

Примечание. «VctAns» обозначает «Память результатов векторных вычислений». Подробные сведения см. в разделе «Память результатов векторных вычислений».

Память результатов векторных вычислений

Если результатом вычисления, выполненного в режиме VECTOR, является вектор, появляется экран VctAns, который содержит результат вычисления. Результат также можно присвоить переменной под названием «VctAns».
Переменная VctAns может использоваться в вычислениях, как показано ниже.

Чтобы вставить переменную VctAns в вычисление, нажмите следующие клавиши: (VECTOR)(VctAns).

Нажатие на любую из следующих клавиш при открытом экране VctAns приводит к автоматическому переключению на экран вычислений: , , , . На экране вычислений отображается переменная VctAns, за которой следует оператор или функция в соответствии с нажатой клавишей.

Присвоение и редактирование данных векторной переменной

Важно!

Следующие операции не поддерживаются редактором векторов: , (M-), (STO). Pol, Rec и многооператорные вычисления также не могут быть введены с использованием редактора векторов.

Присвоение новых данных векторной переменной:

1. Нажмите клавиши (VECTOR)(Dim), затем в открывшемся меню выберите векторную переменную, которой необходимо присвоить данные.

2. В следующем открывшемся меню выберите размер (m).

3. Для ввода элементов вектора используйте открывшийся экран редактора векторов.

Пример 2. Для присвоения значений (2, -1, 2) вектору VctC

(VECTOR)(Dim)(VctC)(3)
212

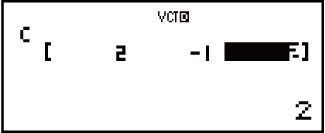
Редактирование элементов векторной переменной:

1. Нажмите клавиши (VECTOR)(Data), затем в открывшемся меню выберите векторную переменную, которой необходимо отредактировать.

2. Для редактирования элементов вектора используйте открывшийся экран редактора векторов.
Переместите курсор в ячейку, содержащую элемент, который необходимо изменить, введите новое значение и нажмите клавишу .

Копирование содержимого векторной величины (или VctAns):

1. Используйте редактор векторов для вывода отображения того вектора, который необходимо скопировать.

Например, чтобы скопировать VctA, необходимо нажать следующие клавиши: (VECTOR)(Data)(VctA).

Если необходимо скопировать содержимое VctAns, выполните следующие действия, чтобы открыть экран VctAns: (VECTOR)(VctAns).

2. Нажмите клавиши (STO), а затем — одно из следующих сочетаний клавиш, чтобы указать целевой вектор для копирования. (VctA), (VctB) или (VctC).

При этом откроется редактор векторов, отображающий содержание целевого вектора для копирования.

Примеры векторных вычислений

В представленных ниже примерах используются векторные переменные VctA = (1, 2) и VctB = (3, 4) из Примера 1, а также векторная переменная VctC = (2, -1, 2) из Примера 2.

Пример 3. 3 × VctA (скалярное умножение векторов), 3 × VctA - VctB (пример вычисления с использованием VctAns)

3(VECTOR)(VctA)

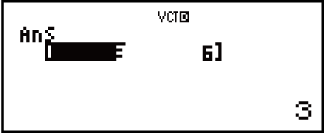
(VECTOR)(VctB)

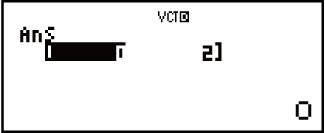
Пример 4. VctA • VctB (скалярное произведение векторов)

(VECTOR)(VctA)
(VECTOR)(Dot)
(VECTOR)(VctB)

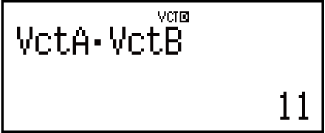
Пример 5. VctA × VctB (обычное произведение векторов)

(VECTOR)(VctA)
(VECTOR)(VctB)

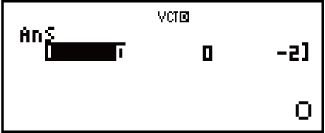
Пример 6. Получение абсолютного значения вектора VctC.

(Abs)
(VECTOR)(VctC)

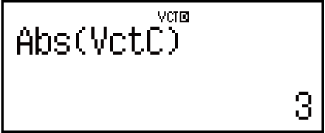
Пример 7. Определение величины угла, образованного векторами VctA и VctB, с точностью до третьего десятичного разряда (Fix 3). (единица измерения углов: Deg)

(cos𝜃 = ^{(𝐴∙𝐵)}_|𝐴||𝐵| становится 𝜃 = cos-1^{(𝐴∙𝐵)}_|𝐴||𝐵|)