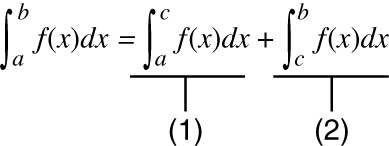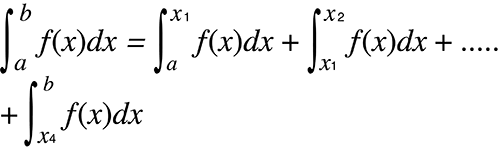Интегральные вычисления

Функция для выполнения численного интегрирования с использованием метода Гаусса-Кронрода.
Синтаксис для ввода при естественном отображении чисел ∫^b_a f (x)dx, синтаксис для ввода при линейном отображении чисел ∫ (f (x), a, b, tol).

tol указывает допустимое отклонение, которое равно 1 × 10-5 при отсутствии введенного значения для tol.

Пример 1. ∫^e₁ ln(x) = 1

(MthIO-MathO)

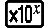(X)1(e)
1

(LineIO)

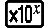(X)(,) 1(,)(e)
1

Пример 2. ∫(¹_x2 , 1, 5, 1 × 10-7) = 0,8 (LineIO)

1(X)(,) 1(,) 5(,)
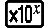
17
0,8

Пример 3. ∫^π₀ (sin x + cos x)2 dx = π (tol: не указано) (MthIO-MathO) (единица измерения углов: Rad)

(X)(X)0
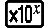(π)
π

Предупреждения об особенностях выполнения интегральных вычислений

Интегральные вычисления можно осуществлять только в режиме COMP.

Следующие клавиши не могут использоваться для f(x), a, b или tol: Pol, Rec, ∫, d/dx, Σ.

При использовании тригонометрической функции в качестве f(x) необходимо указать Rad в качестве единицы измерения углов.

При меньшем значении tol увеличивается точность, но одновременно возрастает продолжительность вычисления. При указании допустимого отклонения tol необходимо использовать значение, которое равно 1 × 10-14 или больше.

Для выполнения интегрирования обычно требуется значительное количество времени.

В зависимости от содержимого f(x) и области интегрирования может генерироваться ошибка вычисления, которая превышает величину допустимого отклонения. В таком случае калькулятор выводит сообщение об ошибке.

Содержимое f(x), положительные и отрицательные значения в пределах интервала интегрирования, а также особенности самого интервала интегрирования могут становиться причиной существенной ошибки в итоговых значениях интегрирования. (Примеры. Наличие частей с точками прерывания или резким изменением. Слишком большой интервал интегрирования.) В таком случае разделение интервала интегрирования на отдельные части и повторное выполнение вычислений может повысить точность.

Советы для успешного выполнения интегральных вычислений

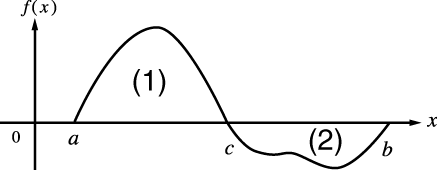
Если периодическая функция или интервал интегрирования предоставляет положительные и отрицательные значения функции f(x)

Выполните независимое интегрирование каждого цикла или положительной и отрицательной частей функции, а затем объедините результаты.

(1) Положительная часть
(2) Отрицательная часть

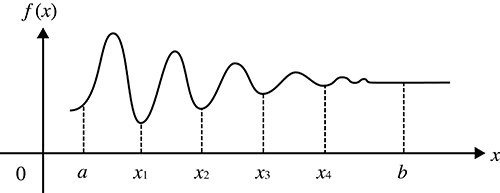
Если интегральные значения колеблются в широком диапазоне вследствие весьма малых сдвигов в интервале интегрирования

Разделите интервал интегрирования на несколько частей (так, чтобы разделить области значительных колебаний на небольшие части), выполните интеграцию каждой части, а затем объедините результаты.