Использование функции SOLVE
Функция SOLVE использует метод Ньютона для округления результатов решения уравнений.
Следует принимать во внимание, что функцию SOLVE можно использовать только в режиме COMP.
Ниже представлены типы уравнений, решения для которых могут быть получены с использованием функции SOLVE.
Уравнения, которые содержат переменную X: X2 + 2X - 2, Y = X + 5, X = sin(M), X + 3 = B + C
функция SOLVE выполняет поиск решения для X. Выражение вида X2 + 2X - 2 обрабатывается как выражение вида X2 + 2X - 2 = 0.
Ввод уравнений с использованием следующего синтаксиса: {уравнение}, {переменная решения}
функция SOLVE выполняет поиск решения для Y, например, если уравнение введено следующим образом: Y = X + 5, Y
Важно!
Если уравнение содержит вводимые функции с открывающими круглыми скобками (например, sin и log), нельзя опускать закрывающие круглые скобки.
Ниже перечислены функции, использование которых внутри уравнения не допускается: ∫, d/dx, Σ, Pol, Rec.
Пример. Поиск решения уравнения y = ax2 + b для x при y = 0, a = 1 и b = -2

 (Y)
(Y)
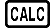 (=)
(=)
 (A)
(A)
 (X)
(X)


 (B)
(B)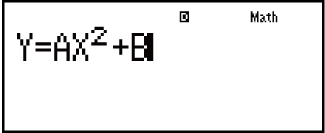

 (SOLVE)
(SOLVE)
(1) Рекомендации по вводу значения для переменной Y
(2) Текущее значение переменной Y
- 0
 1
1
 2
2
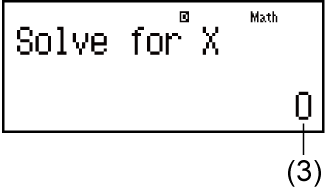
(3) Текущее значение переменной Х
Введите исходное значение для X (здесь введите 1):
- 1

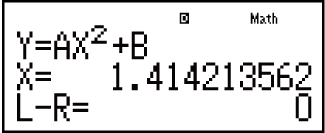
Экран решения
- Для выхода из функции SOLVE:

Примечание
На протяжении всего промежутка времени с момента нажатия клавиши 
 (SOLVE) и до выхода из функции SOLVE путем нажатия клавиши
(SOLVE) и до выхода из функции SOLVE путем нажатия клавиши  необходимо использовать при вводе порядок действий, предусмотренный для линейного отображения чисел.
необходимо использовать при вводе порядок действий, предусмотренный для линейного отображения чисел.
Важно!
В зависимости от содержимого введенного исходного значения переменной X (переменной решения), функция SOLVE может быть неспособна получить решения. В таком случае попробуйте изменить исходное значение переменной для приближения к решению.
Функция SOLVE может быть неспособна найти правильное решение, даже если таковое существует.
Поскольку функция SOLVE использует метод Ньютона, даже при наличии нескольких решений возвращается только одно из них.
Из-за ограничений, присущих методу Ньютона, для уравнений следующего вида сложно получить решения: y = sin(x), y = ex, y = √x.
Содержание экрана решения
Решения всегда отображаются в формате десятичной дроби.

(1) Уравнение (введенное уравнение)
(2) Переменная, для которой выполняется поиск решения
(3) Решение
(4) Результат вычитания (Левая часть) - (Правая часть)
«Результат вычитания (Левая часть) - (Правая часть)» отображается по итогам вычитания правой части уравнения из его левой части после присвоения полученного значения переменной, для которой выполняется поиск решения. Чем ближе полученный результат к нулю, тем точнее решение.
Экран продолжения
Функция SOLVE выполняет сходимость установленное количество раз. Если она неспособна найти решение, на дисплее появляется экран с запросом о подтверждении необходимости продолжения вычислений «Continue: [=]».
Нажмите клавишу  , чтобы продолжить, или клавишу
, чтобы продолжить, или клавишу  для отмены операции SOLVE.
для отмены операции SOLVE.
Пример. Поиск решения уравнения y = x2 - x + 1 для x при y = 3, 7 и 13.

 (Y)
(Y)
 (=)
(=)
 (X)
(X)


 (X)
(X) 1
1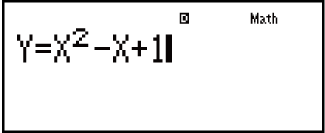

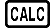 (SOLVE)
(SOLVE)
- 3

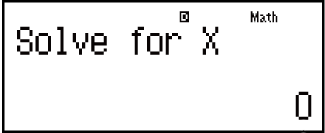
Введите исходное значение для X (здесь введите 1):
- 1

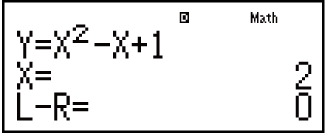
 7
7


 13
13