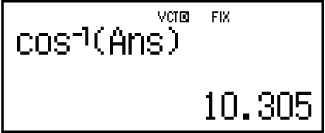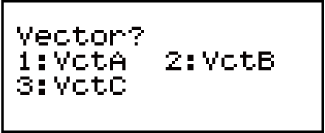Vektorové výpočty (VECTOR)
Režim VECTOR používejte pro provádění výpočtů dvourozměrových a trojrozměrových vektorů. Pro provedení vektorových výpočtů nejprve přiřaďte data ke speciálním vektorovým proměnným (VctA, VctB, VctC) a pak použijte ve výpočtu proměnné, jak je ukázáno v příkladu níže.
Příklad 1: Chcete-li přiřadit (1, 2) k VctA a (3, 4) k VctB a potom provést následující výpočty: (1, 2) + (3, 4)
1. Pro vstup do režimu VECTOR stiskněte klávesu 
 (VECTOR).
(VECTOR).
2. Stiskněte  (VctA)
(VctA) (2).
(2).
Tím se zobrazí Editor vektorů pro vložení dvourozměrového vektoru pro VctA.

(1) „A“ znamená „VctA“.
3. Zadejte prvky VctA: 1 2
2 .
.
4. Proveďte tyto klávesové operace:

 (VECTOR)
(VECTOR) (Data)
(Data) (VctB)
(VctB) (2).
(2).
Tím se zobrazí Editor vektorů pro vložení dvourozměrového vektoru pro VctB.
5. Zadejte prvky VctB: 3 4
4 .
.
6. Stiskem klávesy  přejdete na obrazovku výpočtu a provedete výpočet (VctA+VctB):
přejdete na obrazovku výpočtu a provedete výpočet (VctA+VctB):

 (VECTOR)
(VECTOR) (VctA)
(VctA)

 (VECTOR)
(VECTOR) (VctB)
(VctB) .
.
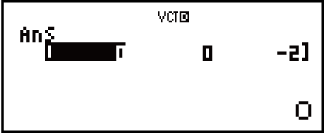
Tím se zobrazí obrazovka VctAns s výsledky výpočtů.

- (2) „Ans“ znamená „VctAns“.
Poznámka: „VctAns“ znamená „paměť posledního výsledku vektoru“ (Vector Answer Memory). Více informací uvádí část „Paměť posledního výsledku vektoru“.
Paměť posledního výsledku vektoru
Kdykoli je výsledkem prováděného výpočtu v režimu VECTOR vektor, objeví se obrazovka VctAns s výsledkem. Výsledek bude také přiřazen k proměnné s názvem „VctAns“.
Proměnná VctAns může být použita ve výpočtech, jak je popsáno níže.
Pro vložení proměnné VctAns do výpočtu proveďte následující klávesovou operaci: 
 (VECTOR)
(VECTOR) (VctAns).
(VctAns).
Stiskem jakékoli z následujících kláves, zatímco je zobrazena obrazovka VctAns, automaticky přepnete na obrazovku výpočtů:  ,
,  ,
,  ,
,  . Obrazovka výpočtů ukáže proměnnou VctAns následovanou operátorem nebo funkcí pro klávesu, kterou jste stiskli.
. Obrazovka výpočtů ukáže proměnnou VctAns následovanou operátorem nebo funkcí pro klávesu, kterou jste stiskli.
Přiřazování a úprava dat vektorové proměnné
Důležité!
Následující operace nejsou podporovány Editorem vektorů:  ,
, 
 (M-),
(M-), 
 (STO). Pol, Rec a několikanásobné výrazy také nemohou být vkládány pomocí Editoru vektorů.
(STO). Pol, Rec a několikanásobné výrazy také nemohou být vkládány pomocí Editoru vektorů.
Přiřazení nových dat vektorové proměnné:
1. Stiskněte 
 (VECTOR)
(VECTOR) (Dim) a poté v nabídce, která se objeví, vyberte vektorovou proměnnou, k níž chcete data přiřadit.
(Dim) a poté v nabídce, která se objeví, vyberte vektorovou proměnnou, k níž chcete data přiřadit.
2. V další nabídce, která se objeví, vyberte rozměr (m).
3. Použijte Editor vektorů, který se objeví, k zadání prvků vektoru.
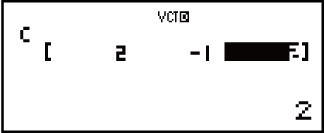
Příklad 2: Chcete-li přiřadit (2, -1, 2) k VctC

 (VECTOR)
(VECTOR) (Dim)
(Dim) (VctC)
(VctC) (3)
(3)
2
 1
1 2
2
Úprava prvků vektorové proměnné:
1. Stiskněte 
 (VECTOR)
(VECTOR) (Data) a poté v nabídce, která se objeví, vyberte vektorovou proměnnou, již chcete upravit.
(Data) a poté v nabídce, která se objeví, vyberte vektorovou proměnnou, již chcete upravit.
2. Použijte Editor vektorů, který se objeví, k úpravě prvků vektoru.
Přemístěte kurzor k buňce, která obsahuje prvek, který chcete změnit, zadejte novou hodnotu a pak stiskněte klávesu  .
.
Kopírování obsahu vektorové proměnné (nebo VctAns):
1. K zobrazení vektoru, který chcete kopírovat, použijte Editor vektorů.
Chcete-li například kopírovat VctA, proveďte následující klávesovou operaci: 
 (VECTOR)
(VECTOR) (Data)
(Data) (VctA).
(VctA).
Chcete kopírovat obsah VctAns, proveďte následující operaci, abyste zobrazili obrazovku VctAns: 

 (VECTOR)
(VECTOR) (VctAns)
(VctAns) .
.
2. Stiskněte 
 (STO) a poté proveďte jednu z následujících klávesových operací ke specifikování cílového místa pro umístění kopie:
(STO) a poté proveďte jednu z následujících klávesových operací ke specifikování cílového místa pro umístění kopie:  (VctA),
(VctA),  (VctB) nebo
(VctB) nebo  (VctC).
(VctC).
Tím se zobrazí Editor vektorů s obsahem cílového místa pro umístění kopie.
Příklady vektorového výpočtu
Níže uvedené příklady používají VctA = (1, 2) a VctB = (3, 4) z příkladu 1 a VctC = (2, -1, 2) z příkladu 2.
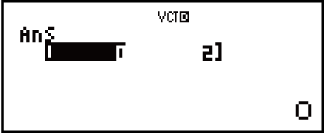
Příklad 3: 3 × VctA (násobení vektorové jednorozměrné veličiny), 3 × VctA - VctB (výpočtový příklad používá VctAns)
 3
3

 (VECTOR)
(VECTOR) (VctA)
(VctA)
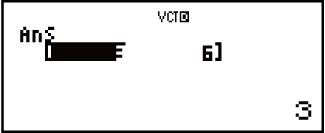


 (VECTOR)
(VECTOR) (VctB)
(VctB)
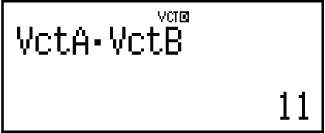
Příklad 4: VctA • VctB (Vektorový skalární součin)


 (VECTOR)
(VECTOR) (VctA)
(VctA)

 (VECTOR)
(VECTOR) (Dot)
(Dot)

 (VECTOR)
(VECTOR) (VctB)
(VctB)
Příklad 5: VctA × VctB (Vektorový součin vektorů)


 (VECTOR)
(VECTOR) (VctA)
(VctA)

 (VECTOR)
(VECTOR) (VctB)
(VctB)
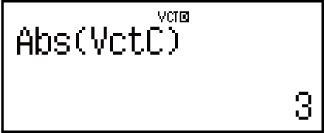
Příklad 6: Získejte absolutní hodnotu VctC.


 (Abs)
(Abs)

 (VECTOR)
(VECTOR) (VctC)
(VctC)

Příklad 7: Určete úhel vytvořený VctA a VctB na tři desetinná místa (Fix 3). (Úhlová jednotka: Deg)
(cos𝜃 = (𝐴∙𝐵) |𝐴||𝐵|, který přejde na 𝜃 = cos-1(𝐴∙𝐵) |𝐴||𝐵|)

 (SETUP)
(SETUP) (Fix)
(Fix)



 (VECTOR)
(VECTOR) (VctA)
(VctA)

 (VECTOR)
(VECTOR) (Dot)
(Dot)

 (VECTOR)
(VECTOR) (VctB)
(VctB)



 (Abs)
(Abs)
 (VECTOR)
(VECTOR) (VctA)
(VctA)


 (Abs)
(Abs)
 (VECTOR)
(VECTOR) (VctB)
(VctB)




 (cos-1)
(cos-1)