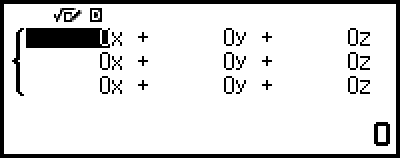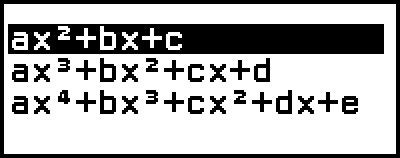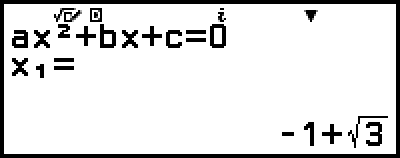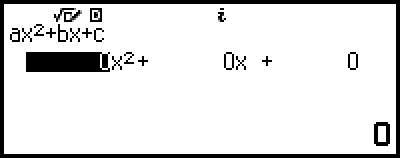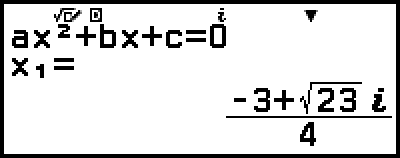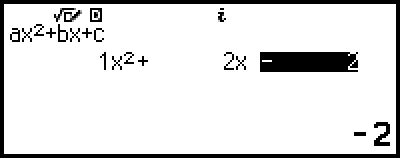方程式计算
方程应用程序包含下面介绍的三个函数。启动应用程序后，可使用出现的方程菜单选择所需函数。
线性方程组：二元到四元联立线性方程
多项式方程：二次到四次高阶方程式
求解方程：用于得出输入方程式中包含的任何变量的值
联立线性方程式
这里，我们将以求解三元联立线性方程为例介绍求解联立方程的一般步骤。
示例 1：
1.按 
，选择方程应用程序图标，然后按 
。
此操作会显示方程菜单。
2.选择 [线性方程组]，然后按 。
此操作将显示元数菜单。
3.选择 [3个未知数]，然后按 。
此操作将显示系数编辑器。
4.使用系数编辑器输入系数值。
- 1
112
1110
1114 
在显示系数编辑器时按 
会将所有系数清零。
5.按 。
此操作将显示解。
显示 
指示符时，每次按 
（或 ）将显示其他解。
- (或 )
- (或 )
显示 
指示符时按 
或 
会使之前显示的解再次出现。
显示最终解时按 会返回系数编辑器。要在显示解时返回系数编辑器，请按 。
在显示系数编辑器时按 会返回元数菜单。
注意
显示系数编辑器时，可将当前突出显示的值存储到变量中。此外，在显示解时，可将当前显示的解存储到变量中。有关变量的详细信息，请参见“变量（A、B、C、D、E、F、x、y、z）”。
二次到四次高阶方程式
使用方程应用程序求解高阶方程时，会根据方程次数显示以下值。
二次方程
显示 ax2+bx+c=0 的解之后，会显示 y=ax2+bx+c 的 最小（或最大）坐标 (x, y)。
三次方程
显示 ax3+bx2+cx+d=0 的解后，仅当存在局部最小值或局部最大值时，显示 y=ax3+bx2+cx+d 的 局部最小值（或局部最大值）的坐标 (x, y)。如果不存在局部最小值或局部最大值，显示最后一个解时按 会出现“无极值”消息。
四次方程
显示 ax4+bx3+cx2+dx+e=0 的解。
这里，我们以二次方程为例介绍求解高阶方程的一般步骤。
示例 2：x2 + 2x − 2 = 0
（输入/输出：数学输入/数学输出）
1.按 ，选择方程应用程序图标，然后按 。
此操作会显示方程菜单。
2.选择 [多项式方程]，然后按 。
此操作将显示次数菜单。
3.选择 [ax2+bx+c]，然后按 。
此操作将显示系数编辑器。
4.使用系数编辑器输入系数值。
- 122
在显示系数编辑器时按 会将所有系数清零。
5.按 。
此操作将显示解。
显示 指示符时，每次按 （或 ）将显示其他计算结果（解或坐标）。
- (或 )
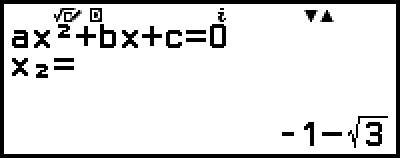
（显示 y = x2 + 2x − 2 的最小值的 x 坐标。）
- (或 )
（显示 y = x2 + 2x − 2 的最小值的 y 坐标。）
- (或 )
显示 指示符时按 或 会使之前显示的计算结果再次出现。
显示最终计算结果时按 会返回系数编辑器。要在显示任一计算结果时返回系数编辑器，请按 。
在显示系数编辑器时按 会返回次数菜单。
注意
显示系数编辑器时，可将当前突出显示的值存储到变量中。显示计算结果（解或坐标）时，也可将其存储到变量中。有关变量的详细信息，请参见“变量（A、B、C、D、E、F、x、y、z）”。
复数解显示（复数根）
高阶方程可能有复数解。在方程菜单上选择多项式方程时，可通过以下操作启用或禁用复数解显示。
– [复数根] > [开]
启用复数解显示（初始缺省设置）。
– [复数根] > [关]
禁用复数解显示。输入和执行有一个或多个复数解的方程仅会导致出现“无实根”消息。
示例 3：2x2 + 3x + 4 = 0
（输入/输出：数学输入/数学输出、复数结果：a+bi，复数根：开）
1.按 ，选择方程应用程序图标，然后按 。
此操作会显示方程菜单。
2.选择 [多项式方程] > [ax2+bx+c]。
此操作将显示系数编辑器。
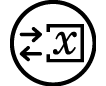
3.使用系数编辑器输入系数值。
- 234
4.按 。
此操作将显示解。
5.显示其他解和坐标值。
- (或 )
- (或 )
- (或 )
显示最终计算结果时按 会返回系数编辑器。要在显示任一计算结果时返回系数编辑器，请按 。
将复数解转换为直角坐标或极坐标
可使用按 
时出现的格式菜单将复数解转换为直角坐标或极坐标格式。
示例 4：将示例 3 中显示的复数解转换为极坐标格式，然后再转换为直角坐标格式
1.执行示例 3 的步骤 1 到 4。
2.按 ，选择 [极坐标形式(r∠θ)]，然后按 。
此操作会将解转换为极坐标格式。
3.按 ，选择 [代数形式(a+bi)]，然后按 。
此操作会将解转换为直角坐标格式。
使用求解方程
求解方程使用牛顿法得出方程的近似解。求解方程支持输入以下格式的方程式。
示例：y = x + 5、x = sin(A)、xy + C（可视为 xy + C = 0）
示例 5：求 x2 - B2 = 0 中 x 的解 (B = 4)
（输入/输出：数学输入/数学输出）
注意
求 x2 - B2 = 0 中 x 的解之前，需要将 4 存储到变量 B。此操作在以下程序的步骤 3 中完成。
1.按 ，选择方程应用程序图标，然后按 。
此操作会显示方程菜单。
2.选择 [求解方程]，然后按 。
此操作会显示求解方程方程式输入屏幕。
3.此处，将 4 存储到变量 B。
4.输入方程式。
(B)
2
(=)*0
* 您也可以使用以下操作输入 = 号：
– [方程] > [=]。
5.按 注册输入方程式。
6.在出现的求解目标屏幕上，确认已选择 [x]，然后按 。
此操作会显示包含 x 初始值的屏幕。
7.输入 1 作为 x 的初始值。
- 1
8.确保已选择 [执行] 后，按 对方程式求解。
(1) 要求的变量
(2) 解
(3) (左侧) − (右侧) 结果
解始终以小数格式显示。
(左侧) − (右侧) 结果越接近 0，解的精确度越高。
9.接下来，按用于执行所需操作的键。
| 要执行此操作： | 按此键： |
|---|---|
| 返回至步骤 6 中的屏幕。 | * |
| 存储输入表达式并返回到步骤 4 中的屏幕。 | 或 |
* 按此键时的初始值会成为最后为计算使用的初始值。
重要事项！
-
求解方程会执行预设次数的收敛。如果无法得出解，则会显示类似于附近屏幕的确认屏幕，询问您是否要继续。在选择 [继续] 的同时按
以继续，或选择 [退出]，然后选择 取消求解方程操作。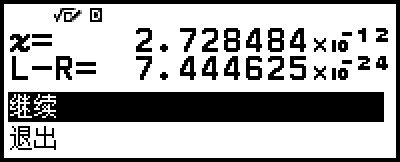 
根据为解变量（上例中的 x）输入的不同初始值，求解方程可能无法得出解。如果无法得出解，请更改初始值，使它们接近解。
求解方程可能无法确定正确的解（即使这种解存在）。
求解方程使用牛顿法，即使存在多个解，计算器只会返回其中一个解。
由于牛顿法的限制，很难对以下类似方程式求解：y=sinx、y=ex、y=√x。
对方程应用程序使用运算验证
方程应用程序允许为联立方程或高阶方程使用运算验证。为方程应用程序启用运算验证后，解的位置会出现下图所示的答案菜单。
您使用此菜单输入答案后（选择 [输入解]，然后再输入解，或选择 [无解] 或 [无数解]），计算器将确定您的答案是否正确。
注意
选择线性方程组时，会出现以上菜单。如果选择多项式方程，将出现其他菜单。
可对各种计算器应用程序使用运算验证。执行本部分中的操作之前，请先阅读“运算验证概述”中的信息。
运算验证不能用于以下方程应用程序函数。
- [线性方程组] > [3个未知数] 或 [4个未知数]
- [多项式方程] > [ax3+bx2+cx+d] 或 [ax4+bx3+cx2+dx+e]
- [求解方程]
如果在运算验证启用时选择方程菜单上的上述任一菜单项，显示屏上会出现“运算验证不可用”消息。
运算验证操作示例
示例 6：输入在示例 2 中求解的方程式 x2 + 2x - 2 = 0 的两个解（x1 = -1 + √3，x2 = -1 - √3），确定其是否正确。此外，选择此方程是否有最小值或最大值，输入坐标值 (x, y)，然后确定数值是否正确。
1.执行示例 2 的步骤 1 到 4。
2.要启用运算验证，请按 ，然后选择 [运算验证开启]。
指示符会出现在屏幕顶部，指示运算验证已启用。
3.按 。
此操作会显示二次方程答案菜单。
4.确认已选择 [解]，然后按 。
此操作将显示解数菜单。
5.这里选择 [2个解]，然后按 。
6.在出现的解输入屏幕上，输入 x1 和 x2。
- 1
3
13 
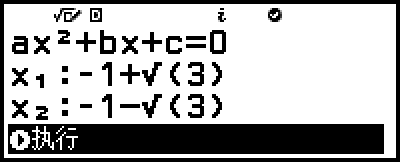
7.确认已选择 [执行]，然后按 。
如果解数和所有输入的解均正确，显示屏上会出现“True”。
如果解数或输入的解错误，显示屏上会出现“False”。按 或 可返回解输入屏幕并再次输入数值。要更改选择的解数，请按解输入屏幕上的 ，并从步骤 4 开始重新执行操作。
8.确认已选择 [返回方程]，然后按 。
随即会返回此操作步骤 1 中的系数编辑器。
9.按 显示答案菜单，然后选择 [最大值] 或 [最小值]。
方程 x2 + 2x - 2 = 0 有最小值，故选择 [最小值]，然后按 。
10.在出现的坐标值输入屏幕上，输入 x 和 y。
- 1
3 
11.确认已选择 [执行]，然后按 。
如果最大值或最小值选择以及所有输入的坐标值均正确，显示屏上会出现“True”。
如果最大值或最小值选择、或输入的坐标值不正确，显示屏上会出现“False”。如果出现这种情况，按 或 可返回坐标值输入屏幕并再次输入数值。要更改最大值/最小值选择，请按坐标值输入屏幕上的 ，从步骤 9 开始重新执行操作。
12.确认已选择 [返回方程]，然后按 。
随即会返回此操作步骤 1 中的系数编辑器。
13.要禁用运算验证并退出运算验证操作，请按 ，然后选择 [运算验证关闭]。
随后， 指示符会从屏幕上消失。
有关如何禁用运算验证的信息，请参见“禁用运算验证”。
注意
要查看解和最小值，可在此操作的步骤 8 或步骤 12 中选择 [确认解]，然后按 。出现的屏幕以及可执行操作与示例 2 的步骤 5 相同。
