CASIO

Les exemples suivants utilisent VctA = (1, 2) et VctB = (3, 4) de l’Exemple 1, et VctC = (2, -1, 2) de l’Exemple 2. Vous pouvez saisir une variable de vecteur dans une opération de touches en appuyant sur (VCT)(Vct) puis en appuyant sur une des touches numériques suivantes : (A), (B), (C).

Exemple 3 : 3 × VctA = (3, 6) (multiplication scalaire de vecteurs), 3 × VctA - VctB = (0, 2) (exemple de calcul utilisant VctAns)

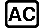• 3 VctA
• 

• VctB
• 

Exemple 4 : VctA • VctB (produit scalaire de vecteurs)

• VctA (VCT)(Dot) VctB
• 

Exemple 5 : VctA × VctB = (0, 0, -2) (produit croisé de vecteurs)

• VctA VctB
• 

Exemple 6 : Obtenir les valeurs absolues de VctC.

• (Abs) VctC
• 

Exemple 7 : Déterminez l’angle constitué par VctA et VctB avec trois décimales (Fix 3).　(Unité d’angle : Deg) (, qui devient )

• ･････(Fix) VctA (VCT)(Dot) VctB
  (Abs) VctA (Abs) VctB

• 

• (cos-1)
•