fx-95MS/fx-500MS/
(2nd edition / S-V.P.A.M.)
Before Using the Calculator
Calculation Modes and Calculator Setup
Basic Calculations
- ▶Inputting Expression and Values
- ▶Arithmetic Calculations
- ▶Fraction Calculations
- ▶Percent Calculations
- ▶Degree, Minute, Second (Sexagesimal) Calculations
- ▶Multi-Statements
- ▶Using Engineering Notation
- ▶Calculation History and Replay
- ▶Using Memory Functions
Function Calculations
- ▶Pi (π), Natural Logarithm Base e
- ▶Trigonometric Functions, Inverse Trigonometric Functions
- ▶Hyperbolic Functions, Inverse Hyperbolic Functions
- ▶Angle Unit Conversion
- ▶Exponential Functions, Logarithmic Functions
- ▶Power Functions and Power Root Functions
- ▶Rectangular-Polar Coordinate Conversion
- ▶Factorial (!)
- ▶Random Number (Ran#)
- ▶Permutation (nPr) and Combination (nCr)
- ▶Rounding function (Rnd)
Using Calculation Modes
Technical Information
Statistical Calculations (SD, REG)
Regression Calculations (REG)
Use the  key to enter the REG Mode when you want to perform statistical calculations using regression.
key to enter the REG Mode when you want to perform statistical calculations using regression.

 (REG)
(REG)
In the SD Mode and REG Mode, the  key operates as the
key operates as the  key.
key.
Entering the REG Mode displays screens like the ones shown below.
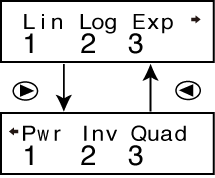
Press the number key ( ,
,  , or
, or  ) that corresponds to the type of regression you want to use.
) that corresponds to the type of regression you want to use.
 (Lin) : Linear regression
(Lin) : Linear regression
 (Log) : Logarithmic regression
(Log) : Logarithmic regression
 (Exp) : Exponential regression
(Exp) : Exponential regression

 (Pwr) : Power regression
(Pwr) : Power regression

 (Inv) : Inverse regression
(Inv) : Inverse regression

 (Quad) : Quadratic regression
(Quad) : Quadratic regression
Always start data input with 
 (CLR)
(CLR) (Scl)
(Scl) to clear statistical memory.
to clear statistical memory.
Input data using the key sequence shown below.
<x-data> <y-data>
<y-data>
The values produced by a regression calculation depend on the values input, and results can be recalled using the key operations shown in the table below.
| To recall this type of value: | Perform this key operation: |
|---|---|
| Σx2 |   (S-SUM) (S-SUM) (Σx2) (Σx2) |
| Σx |   (S-SUM) (S-SUM) (Σx) (Σx) |
| n |   (S-SUM) (S-SUM) (n) (n) |
| Σy2 |   (S-SUM) (S-SUM)  (Σy2) (Σy2) |
| Σy |   (S-SUM) (S-SUM)  (Σy) (Σy) |
| Σxy |   (S-SUM) (S-SUM)  (Σxy) (Σxy) |
| x- |   (S-VAR) (S-VAR) (x-) (x-) |
| σx |   (S-VAR) (S-VAR) (σx) (σx) |
| sx |   (S-VAR) (S-VAR) (sx) (sx) |
| y- |   (S-VAR) (S-VAR)  (y-) (y-) |
| σy |   (S-VAR) (S-VAR)  (σy) (σy) |
| sy |   (S-VAR) (S-VAR)  (sy) (sy) |
| Regression coefficient A |   (S-VAR) (S-VAR)   (A) (A) |
| Regression coefficient B |   (S-VAR) (S-VAR)   (B) (B) |
| Regression calculation other than quadratic regression | |
| Correlation coefficient r |   (S-VAR) (S-VAR)   (r) (r) |
| xˆ |   (S-VAR) (S-VAR)    (xˆ) (xˆ) |
| yˆ |   (S-VAR) (S-VAR)    (yˆ) (yˆ) |
The following table shows the key operations you should use to recall results in the case of quadratic regression.
| To recall this type of value: | Perform this key operation: |
|---|---|
| Σx3 |   (S-SUM) (S-SUM)   (Σx3) (Σx3) |
| Σx2y |   (S-SUM) (S-SUM)   (Σx2y) (Σx2y) |
| Σx4 |   (S-SUM) (S-SUM)   (Σx4) (Σx4) |
| Regression coefficient C |   (S-VAR) (S-VAR)   (C) (C) |
| xˆ1 |   (S-VAR) (S-VAR)    (xˆ1) (xˆ1) |
| xˆ2 |   (S-VAR) (S-VAR)    (xˆ2) (xˆ2) |
| yˆ |   (S-VAR) (S-VAR)    (yˆ) (yˆ) |
The values in the above tables can be used inside of expressions the same way you use variables.
Linear Regression
The regression formula for linear regression is: y = A + Bx.
Example: Atmospheric Pressure vs. Temperature
Perform linear regression to determine the regression formula terms and correlation coefficient for the data below.
| Temperature | Atmospheric Pressure |
|---|---|
| 10°C | 1003 hPa |
| 15°C | 1005 hPa |
| 20°C | 1010 hPa |
| 25°C | 1011 hPa |
| 30°C | 1014 hPa |
Next, use the regression formula to estimate atmospheric pressure at -5°C and temperature at 1000 hPa. Finally, calculate the coefficient of determination (r2) and sample covariance (∑xy - n∙x-∙y-n - 1).
-
In the REG Mode:
 (Lin)
(Lin)

 (CLR)
(CLR) (Scl)
(Scl) (Stat clear)10
(Stat clear)10 1003
1003

Each time you press  to register your input, the number of data input up to that point is indicated on the display (n value).
to register your input, the number of data input up to that point is indicated on the display (n value).
15 1005
1005 20
20 1010
1010 25
25 1011
1011 30
30 1014
1014
Regression Coefficient A = 997.4

 (S-VAR)
(S-VAR)

 (A)
(A)
- 997.4
Regression Coefficient B = 0.56

 (S-VAR)
(S-VAR)

 (B)
(B)
- 0.56
Correlation Coefficient r = 0.982607368

 (S-VAR)
(S-VAR)

 (r)
(r)
- 0.982607368
Atmospheric Pressure at 5°C = 994.6

 5
5

 (S-VAR)
(S-VAR)


 (yˆ)
(yˆ)
- 994.6
Temperature at 1000 hPa = 4.642857143
- 1000

 (S-VAR)
(S-VAR)


 (xˆ)
(xˆ)
- 4.642857143
Coefficient of Determination = 0.965517241

 (S-VAR)
(S-VAR)

 (r)
(r)

- 0.965517241
Sample Covariance = 35


 (S-SUM)
(S-SUM)
 (Σxy)
(Σxy)

 (S-SUM)
(S-SUM) (n)
(n)

 (S-VAR)
(S-VAR) (x-)
(x-)

 (S-VAR)
(S-VAR)
 (y-)
(y-)



 (S-SUM)
(S-SUM) (n)
(n) 1
1

- 35.
Logarithmic, Exponential, Power, and Inverse Regression
Use the same key operations as linear regression to recall results for these types of regression.
The following shows the regression formulas for each type of regression.
| Logarithmic Regression | y = A + B・ln x |
|---|---|
| Exponential Regression | y = A・eB•x (ln y = ln A + Bx) |
| Power Regression | y = A・xB (ln y = ln A + Bln x) |
| Inverse Regression | y = A + B・1/x |
Quadratic Regression
The regression formula for quadratic regression is: y = A + Bx + Cx2.
Example:
Perform quadratic regression to determine the regression formula terms for the data below.
| xi | yi |
|---|---|
| 29 | 1.6 |
| 50 | 23.5 |
| 74 | 38.0 |
| 103 | 46.4 |
| 118 | 48.0 |
Next, use the regression formula to estimate the values for yˆ (estimated value of y) for xi = 16 and xˆ (estimated value of x) for yi = 20.
In the REG Mode:

 (Quad)
(Quad)

 (CLR)
(CLR) (Scl)
(Scl) (Stat clear)
(Stat clear)
29 1
1 6
6 50
50 23
23 5
5 74
74 38
38 0
0 103
103 46
46 4
4 118
118 48
48 0
0
Regression Coefficient A = -35.59856934

 (S-VAR)
(S-VAR)

 (A)
(A)
- -35.59856934
Regression Coefficient B = 1.495939413

 (S-VAR)
(S-VAR)

 (B)
(B)
- 1.495939413
Regression Coefficient C = -6.71629667 × 10-3

 (S-VAR)
(S-VAR)

 (C)
(C)
- -6.71629667×10-3
yˆ when xi is 16 = -13.38291067
- 16

 (S-VAR)
(S-VAR)


 (yˆ)
(yˆ)
- -13.38291067
xˆ1 when yi is 20 = 47.14556728
- 20

 (S-VAR)
(S-VAR)


 (xˆ1)
(xˆ1)
- 47.14556728
xˆ2 when yi is 20 = 175.5872105
- 20

 (S-VAR)
(S-VAR)


 (xˆ2)
(xˆ2)
- 175.5872105
Data Input Precautions

 inputs the same data twice.
inputs the same data twice.
You can also input multiple entries of the same data using 
 (;). To input the data "20 and 30" five times, for example, press 20
(;). To input the data "20 and 30" five times, for example, press 20  30
30 
 (;) 5
(;) 5 .
.
The above results can be obtained in any order, and not necessarily that shown above.
Precautions when editing data input for standard deviation also apply for regression calculations.
Do not use variables A through F, X, or Y to store data when performing statistical calculations. These variables are used for statistical calculation temporary memory, so any data you may have assigned to them may be replaced by other values during statistical calculations.
Entering the REG Mode and selecting a regression type (Lin, Log, Exp, Pwr, Inv, Quad) clear variables A through F, X, and Y. Changing from one regression type to another inside the REG Mode also clears these variables.