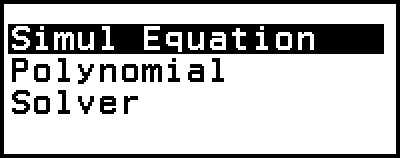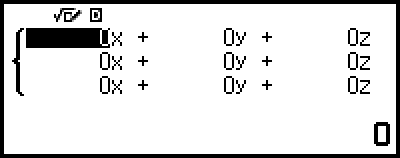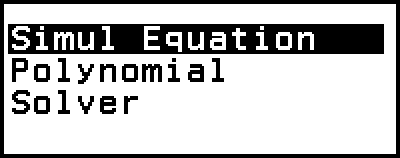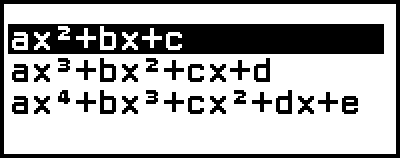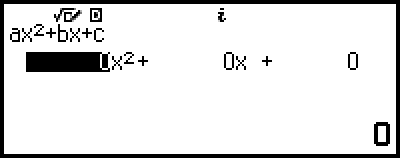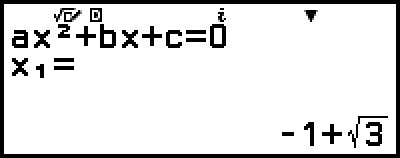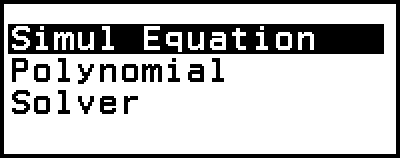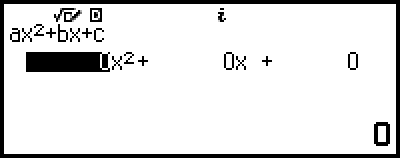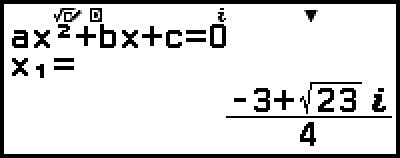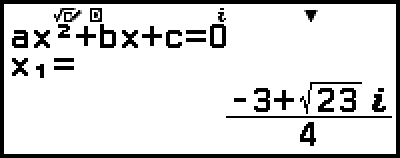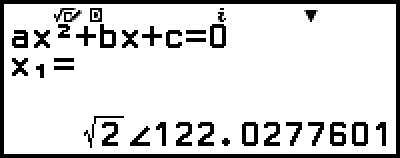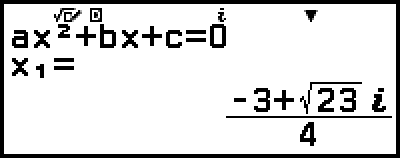Ekvationsberäkningar
Equation-läget har de tre funktionerna som beskrivs nedan. När du har startat läget kan du använda Equation-menyn som visas för att välja den funktion du vill.
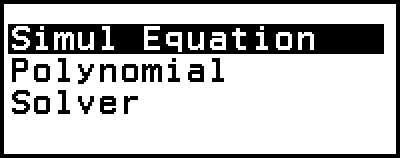
Simul Equation: Simultana linjära ekvationer med två till fyra okända
Polynomial: Höggradsekvationer från 2:a till 4:e graden
Solver: Funktion för att hitta värdet på en variabel som finns i en inmatad ekvation
Simultana linjära ekvationer
Här förklarar vi den allmänna proceduren för att lösa en simultan ekvation med ett exempel där vi tar upp en simultan linjär ekvation med tre okända.
Exempel 1: 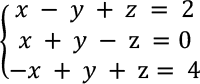
1. Tryck på  , välj ikonen för Equation-läget och tryck sedan på
, välj ikonen för Equation-läget och tryck sedan på  .
.
Då visas Equation-menyn.
2. Välj [Simul Equation] och tryck sedan på  .
.
Då visas menyn för okända.
3. Välj [3 Unknowns] och tryck sedan på  .
.
Då visas koefficientredigeraren.
4. Använd koefficientredigeraren för att ange koefficientvärdena.
- 1


 ((-))1
((-))1 1
1 2
2
1 1
1

 ((-))1
((-))1 0
0

 ((-))1
((-))1 1
1 1
1 4
4
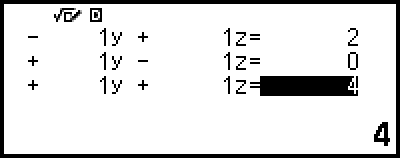
Om du trycker på  när koefficientredigeraren visas så rensas alla koefficienter och nollställs.
när koefficientredigeraren visas så rensas alla koefficienter och nollställs.
5. Tryck på  .
.
Då visas en lösning.
När indikatorn  visas så kan du visa en ny lösning för varje tryck på
visas så kan du visa en ny lösning för varje tryck på  (eller
(eller  ).
).
 (eller
(eller  )
)
 (eller
(eller  )
)
Om du trycker på  eller
eller  medan indikatorn
medan indikatorn  visas så dyker den lösning som visades tidigare upp igen.
visas så dyker den lösning som visades tidigare upp igen.
Om du trycker på  medan den slutliga lösningen visas återgår du till koefficientredigeraren. Om du vill gå tillbaka till koefficientredigeraren medan lösningen visas trycker du på
medan den slutliga lösningen visas återgår du till koefficientredigeraren. Om du vill gå tillbaka till koefficientredigeraren medan lösningen visas trycker du på  .
.
Om du trycker på  när koefficientredigeraren visas återgår du till menyn för antal okända.
när koefficientredigeraren visas återgår du till menyn för antal okända.
Obs!
När koefficientredigeraren visas kan du lagra det aktuella markerade värdet till en variabel. När lösningen visas går det också bra att lagra aktuellt visad lösning till en variabel. Mer information om variabler hittar du i ”Variabler (A, B, C, D, E, F, x, y, z)”.
Höggradsekvationer från 2:a till 4:e graden
När du löser en höggradsevkation med Equation-läget så visas värdena nedan enligt ekvationens grad.
Kvadratisk ekvation
Efter att lösningen för ax2+bx+c=0 har visats så visas de minsta (eller högsta) koordinaterna (x, y) för y=ax2+bx+c.
Kubisk ekvation
Efter visning av lösningen på ax3+bx2+cx+d=0 så visas koordinaterna (x, y) för lokala minsta (eller lokala högsta) värde y=ax3+bx2+cx+d, endast om det finns ett lokalt minsta eller högsta värde. Om det inte finns ett lokalt minsta eller lokalt högsta värde så visas meddelandet No Local Max/Min om du trycker på  .
.
Kvadratisk ekvation
Lösningen för ax4+bx3+cx2+dx+e=0 visas.
Här visar vi ett exempel på en kvadratisk ekvation för att förklara den allmänna proceduren för att lösa en höggradsekvation.
Exempel 2: x2 + 2x − 2 = 0
(Input/Output: MathI/MathO)
1. Tryck på  , välj ikonen för Equation-läget och tryck sedan på
, välj ikonen för Equation-läget och tryck sedan på  .
.
Då visas Equation-menyn.
2. Välj [Polynomial] och tryck sedan på  .
.
Då visas menyn för grader.
3. Välj [ax2+bx+c] och tryck sedan på  .
.
Då visas koefficientredigeraren.
4. Använd koefficientredigeraren för att ange koefficientvärdena.
- 1
 2
2

 ((-))2
((-))2
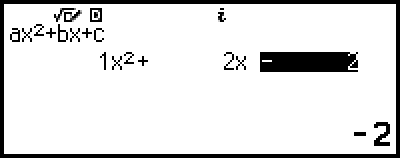
Om du trycker på  när koefficientredigeraren visas så rensas alla koefficienter och nollställs.
när koefficientredigeraren visas så rensas alla koefficienter och nollställs.
5. Tryck på  .
.
Då visas en lösning.
När indikatorn  visas så kan du visa ett nytt beräkningsresultat (lösning eller koordinat) för varje tryck på
visas så kan du visa ett nytt beräkningsresultat (lösning eller koordinat) för varje tryck på  (eller
(eller  ).
).
 (eller
(eller  )
)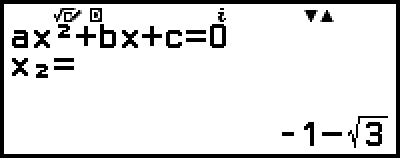
(Visar x-koordinat för minsta värdet för y = x2 + 2x − 2.)
 (eller
(eller  )
)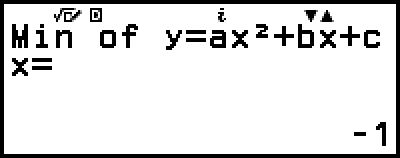
(Visar y-koordinat för minsta värde för y = x2 + 2x − 2.)
 (eller
(eller  )
)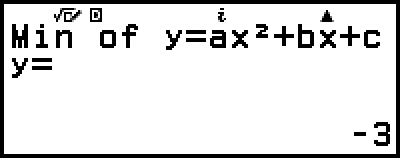
Om du trycker på  eller
eller  medan indikatorn
medan indikatorn  visas så visas den beräkning som visades tidigare igen.
visas så visas den beräkning som visades tidigare igen.
Om du trycker på  medan det slutliga beräkningsresultatet visas återgår du till koefficientredigeraren. Om du vill gå tillbaka till koefficientredigeraren medan beräkningsresultatet visas trycker du på
medan det slutliga beräkningsresultatet visas återgår du till koefficientredigeraren. Om du vill gå tillbaka till koefficientredigeraren medan beräkningsresultatet visas trycker du på  .
.
Om du trycker på  medan koefficientredigeraren visas återgår du till menyn för antal grader.
medan koefficientredigeraren visas återgår du till menyn för antal grader.
Obs!
När koefficientredigeraren visas kan du lagra det aktuella markerade värdet till en variabel. Även om ett beräkningsresultat (lösning eller koordinat) visas kan det lagras i en variabel. Mer information om variabler hittar du i ”Variabler (A, B, C, D, E, F, x, y, z)”.
Visning av komplexa tallösningar (Complex Roots)
Höggradsekvationer kan ha komplexa tallösningar. Om du väljer Polynomial i Equation-menyn kan du använda åtgärderna nedan för att aktivera eller avaktivera visning av komplexa tallösningar.
 – [Complex Roots] > [On]
– [Complex Roots] > [On] 
Aktiverar visning av komplexa tallösningar (initial standardinställning).
 – [Complex Roots] > [Off]
– [Complex Roots] > [Off] 
Avaktiverar visning av komplexa tallösningar. Om du lägger in och kör en ekvation som har en eller flera tallösningar så visas meddelandet No Real Roots.
Exempel 3: 2x2 + 3x + 4 = 0
(Input/Output: MathI/MathO, Complex Result: a+bi, Complex Roots: On)
1. Tryck på  , välj ikonen för Equation-läget och tryck sedan på
, välj ikonen för Equation-läget och tryck sedan på  .
.
Då visas Equation-menyn.
2. Välj [Polynomial] > [ax2+bx+c].
Då visas koefficientredigeraren.
3. Använd koefficientredigeraren för att ange koefficientvärdena.
- 2
 3
3 4
4

4. Tryck på  .
.
Då visas en lösning.
5. Visa en annan lösning och koordinatvärden.
 (eller
(eller  )
)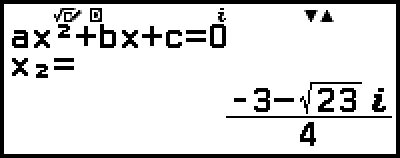
 (eller
(eller  )
)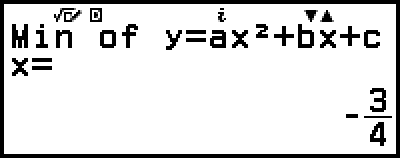
 (eller
(eller  )
)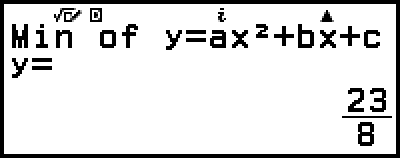
Om du trycker på  medan det slutliga beräkningsresultatet visas återgår du till koefficientredigeraren. Om du vill gå tillbaka till koefficientredigeraren medan beräkningsresultatet visas trycker du på
medan det slutliga beräkningsresultatet visas återgår du till koefficientredigeraren. Om du vill gå tillbaka till koefficientredigeraren medan beräkningsresultatet visas trycker du på  .
.
Konvertera en komplex tallösning till rektangulära eller polära koordinater
Du kan använda FORMAT-menyn som visas när du trycker på  för att konvertera en komplex nummerlösning till en rektangulär koordinat eller polär koordinat.
för att konvertera en komplex nummerlösning till en rektangulär koordinat eller polär koordinat.
Exempel 4: För att konvertera den komplexa tallösningen som visas i Exempel 3 till polärt koordinatformat och sedan till rektangulärt koordinatformat
1. Utför steg 1 till 4 i Exempel 3.
2. Tryck på  , välj [Polar Coord] och tryck sedan på
, välj [Polar Coord] och tryck sedan på  .
.
Då konverteras lösningen till polärt koordinatformat.
3. Tryck på  , välj [Rectangular Coord] och tryck sedan på
, välj [Rectangular Coord] och tryck sedan på  .
.
Då konverteras lösningen till rektangulärt koordinatformat.
Använda Solver
Solver använder Newtons metod för att approximera lösningen av ekvationer. Solver har stöd för inmatning av ekvationer i följande format.
Exempel: y = x + 5, x = sin(A), xy + C (Behandlas som xy + C = 0)
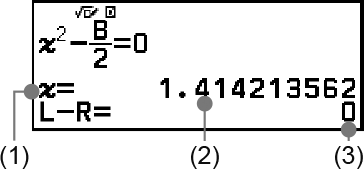
Exempel 5: För att lösa x2 - B2 = 0 for x när B = 4
(Input/Output: MathI/MathO)
Obs!
Innan du löser x2 - B2 = 0 for x måste 4 lagras i variabel B. Detta görs i steg 3 i proceduren nedan.
1. Tryck på  , välj ikonen för Equation-läget och tryck sedan på
, välj ikonen för Equation-läget och tryck sedan på  .
.
Då visas Equation-menyn.
2. Välj [Solver] och tryck sedan på  .
.
Då visas Solver-skärmen för ekvationsinmatning.
3. Här lagrar du 4 till variabel B.
 4
4

Den här åtgärden kan utföras när som helst före steg 7 i den här proceduren.
Mer information om variabler hittar du i ”Variabler (A, B, C, D, E, F, x, y, z)”.
Tryck på  för att återgå till Solver-skärmen för ekvationsinmatning.
för att återgå till Solver-skärmen för ekvationsinmatning.
4. Mata in ekvationen.




 (B)
(B) 2
2

 (=)*0
(=)*0
* Du kan också använda följande åtgärd för att mata in tecknet =.  – [Equation] > [=].
– [Equation] > [=].
5. Tryck på  för att registrera den inmatade ekvationen.
för att registrera den inmatade ekvationen.
6. På Solve Target-skärmen som visas bekräftar du att [x] har valts och trycker sedan på  .
.
Då visas en skärm med det ursprungliga värdet x.
7. Mata in 1 som startvärde på x.
- 1


8. När du har kontrollerat att [Execute] har valts trycker du på  för att lösa ekvationen.
för att lösa ekvationen.
(1) Variabel löst för
(2) Lösning
(3) Resultat på (vänster sida) – (höger sida)
Lösningar visas alltid i decimalform.
Ju närmare resultatet (vänster sida) − (höger sida) är noll desto högre noggrannhet har lösningen.
9. Tryck sedan på den knapp som utför den åtgärd du vill använda.
| Så här gör du: | Tryck på den här tangenten: |
|---|---|
| Gå tillbaka till skärmen i steg 6. |  * * |
| Lagra inmatningsuttrycket och återgå till skärmen i steg 4. |  eller eller  |
* Startvärde när du trycker på den här tangenten blir det initiala värde som du senast använde för beräkningen.
Viktigt!
-
Solver utför konvergens ett förinställt antal gånger. Om du inte kan hitta en lösning visas en bekräftelseskärm som den i närheten och du får frågan om du vill fortsätta. Tryck på
 medan [Continue] är valt för att fortsätta eller välj [Exit] och sedan
medan [Continue] är valt för att fortsätta eller välj [Exit] och sedan  för att avbryta Solver-åtgärden.
för att avbryta Solver-åtgärden. 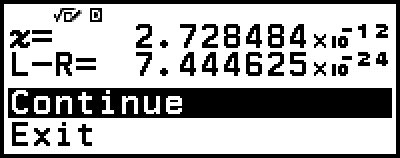
Beroende på vad du anger för det initiala värdet för lösningsvariabeln (x i exemplet ovan) kan det hända att Solver inte kan erhålla en lösning. Om detta händer kan du försöka ändra det ursprungliga värdet så att det ligger närmare lösningen.
Solver kanske inte kan avgöra vilken lösning som är rätt, även om den finns.
Solver använder Newtons metod, så även om det finns flera lösningar kommer endast en av dem att returneras.
På grund av begränsningar i Newtons metod tenderar lösningar att vara svåra att erhålla för följande ekvationer: y=sinx, y=ex, y=√x.