Calculs de nombres complexes
Pour effectuer des calculs de nombres complexes, lancez d’abord l’application Complexes.
Appuyez sur 
, sélectionnez l’icône de l’application Complexes, puis appuyez sur 
.
Saisie de nombres complexes
Vous pouvez utiliser des coordonnées rectangulaires (a+bi) ou les coordonnées polaires (r∠θ) pour saisir des nombres complexes.
Exemple 1 : Pour saisir 2+3i
- 2
3
(i)* 
* Vous pouvez également effectuer l’opération suivante pour saisir i : 
– [Complexes] > [i].
Exemple 2 : Pour saisir 5∠30
- 5 – [Complexes] > [∠] 30
Exemples de calculs de l’application Complexes
Avant d’effectuer les opérations de l’exemple
Pour les exemples de cette section, utilisez le menu CONFIG pour sélectionner Smaths/Rmaths pour le réglage Saisie/Résultat. Configurez les autres réglages comme indiqué pour chaque exemple.
Les résultats du calcul des nombres complexes sont affichés conformément au réglage Forme complexe dans le menu CONFIG.
Si vous prévoyez d’effectuer la saisie et l’affichage du résultat du calcul en format de coordonnées polaires, spécifiez l’Unité d’angle dans le menu CONFIG avant de commencer le calcul.
La valeur θ du résultat du calcul est affiché dans la plage de -180° < θ ≤ 180°.
L’affichage du résultat du calcul lorsque quelque chose d’autre que Smaths/Rmaths est sélectionné indique a et bi (ou r et θ) sur des lignes séparées.
Exemple 3 : (1 + i)4 + (1 - i)2 = -4 - 2i
(Forme complexe : a+bi)
1(i)
4
1
(i)
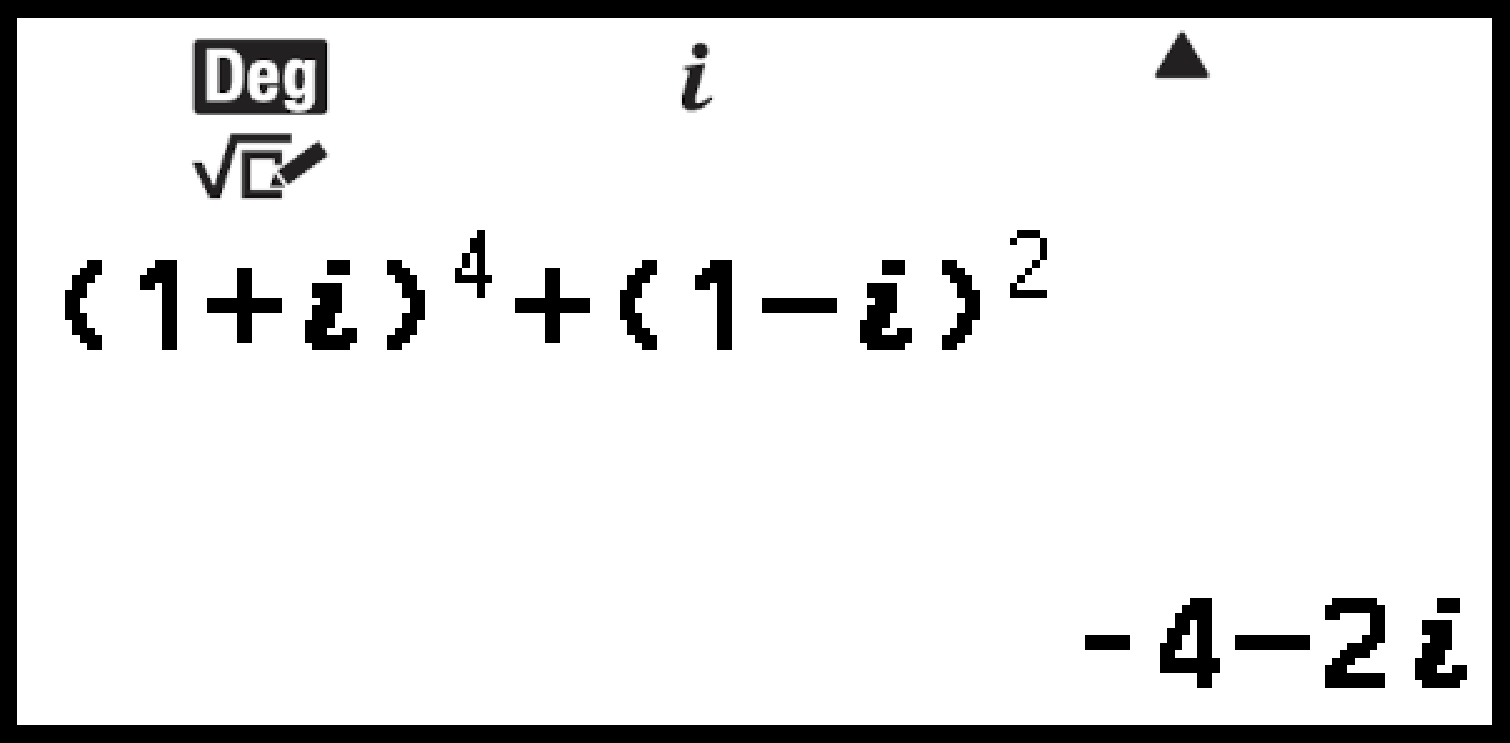
Note
Lorsqu’on élève un nombre complexe à une puissance entière en utilisant la syntaxe (a+bi)n, la valeur de la puissance peut être comprise dans l’intervalle suivant : -1 × 1010 < n < 1 × 1010.
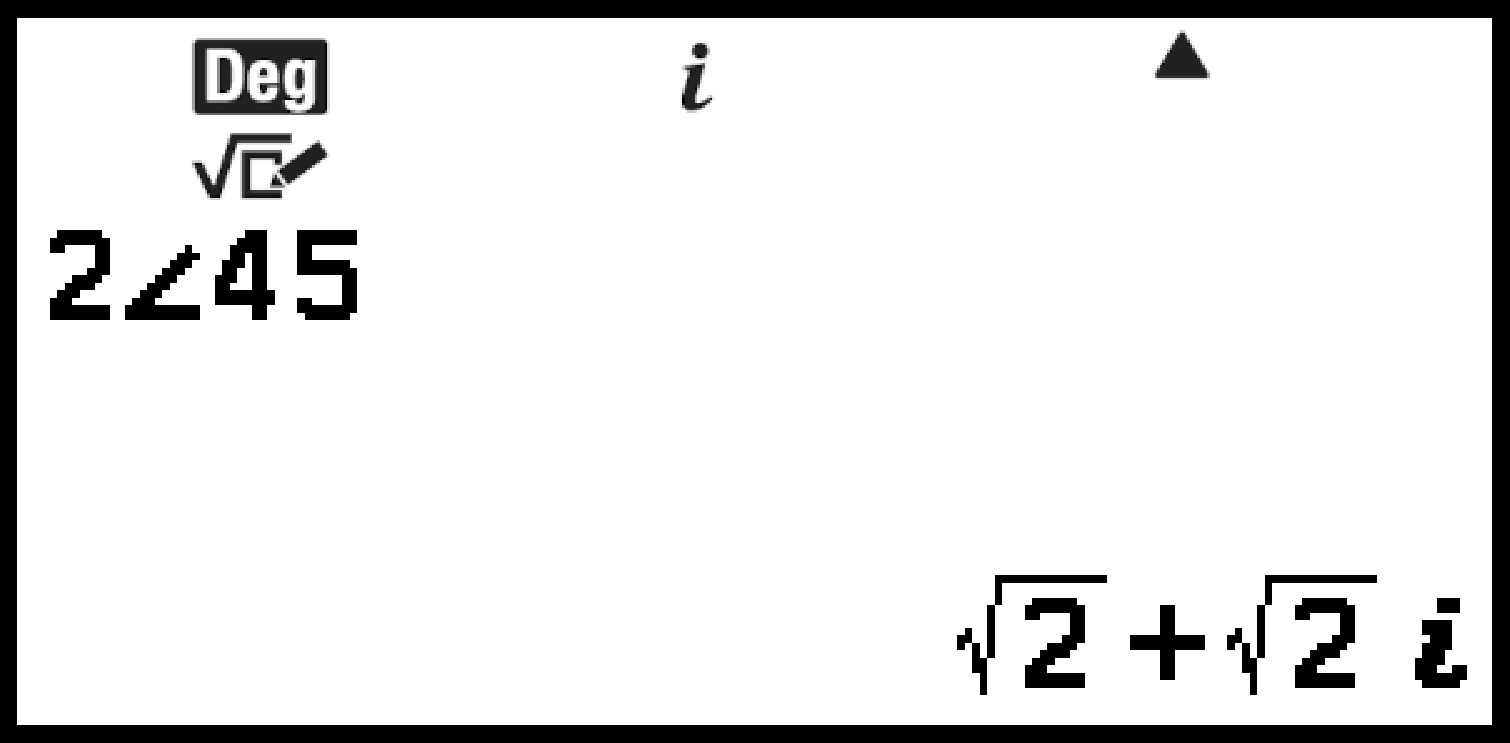
Exemple 4 : 2∠45 = √2 + √2i
(Unité d’angle : Degré, Forme complexe : a+bi)
- 2 – [Complexes] > [∠] 45
Exemple 5 : √2 + √2i = 2∠45
(Unité d’angle : Degré, Forme complexe : r∠θ)
22(i)
Exemple 6 : Pour obtenir le nombre complexe conjugué de 2 + 3i
(Forme complexe : a+bi)
- – [Complexes] > [Conjugué]
23(i) 
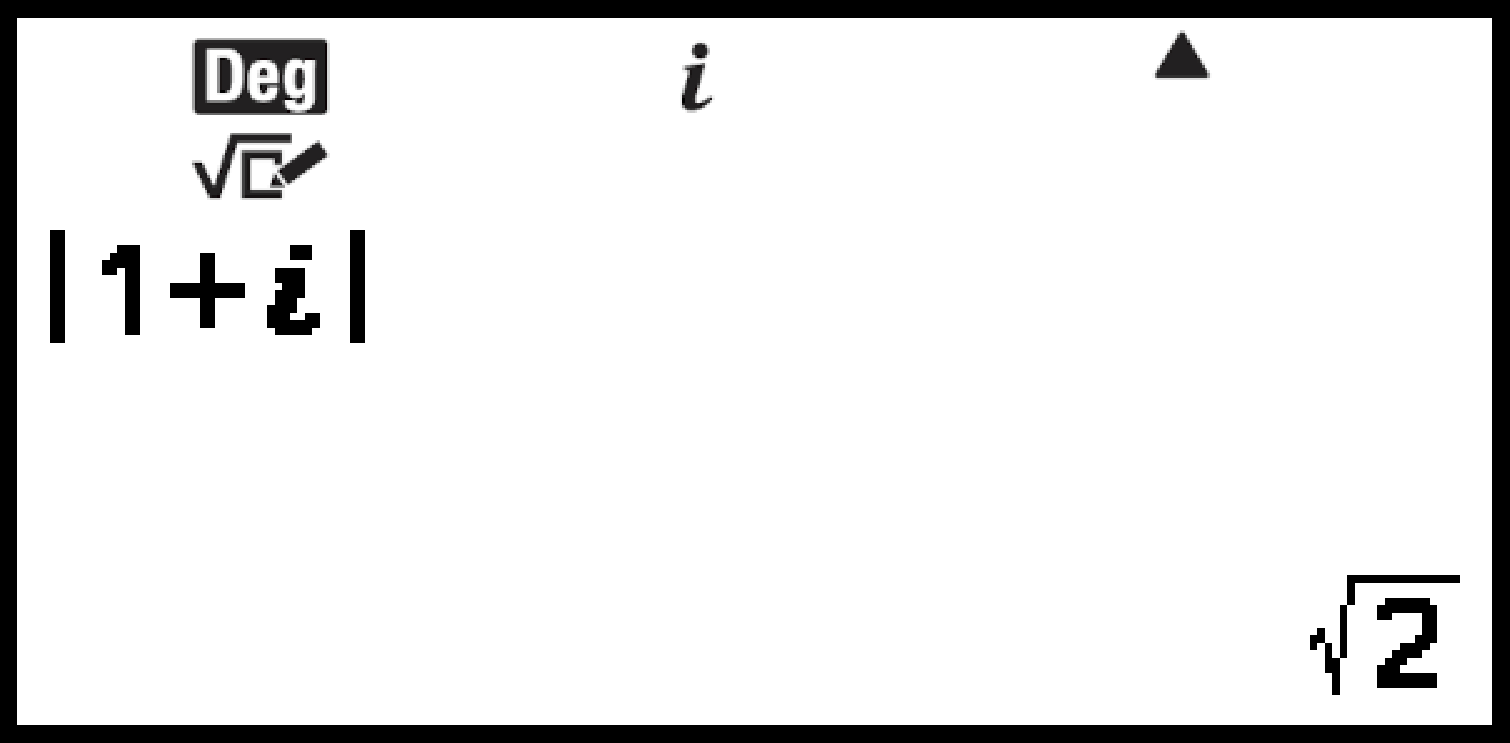
Exemple 7 : Pour obtenir la valeur absolue et l’argument de 1 + i
(Unité d’angle : Degré)
- – [Calcul numérique] > [Valeur absolue]
1(i) 
- – [Complexes] > [Argument]
1(i) 
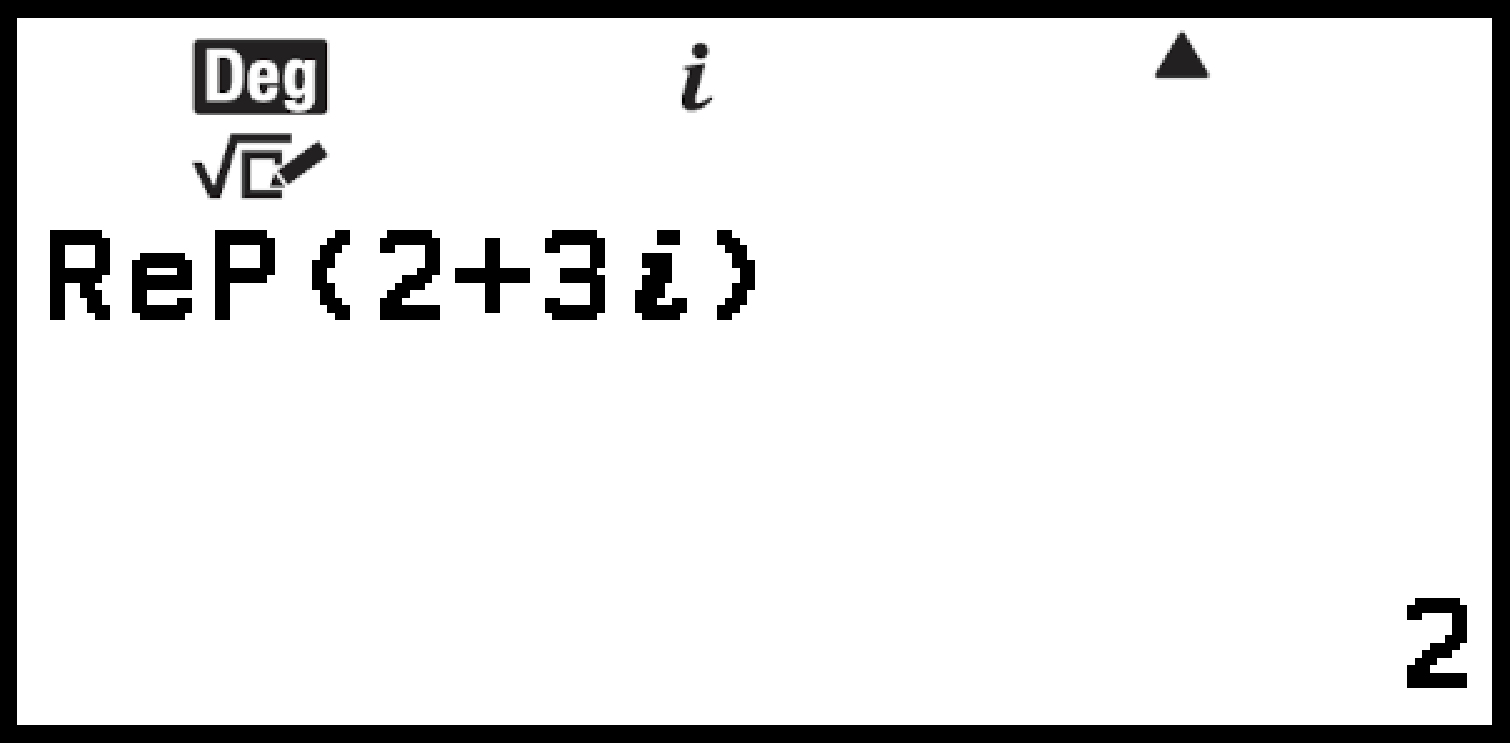
Exemple 8 : Pour extraire la partie réelle et la partie imaginaire de 2 + 3i
- – [Complexes] > [Partie réelle]
23(i) 
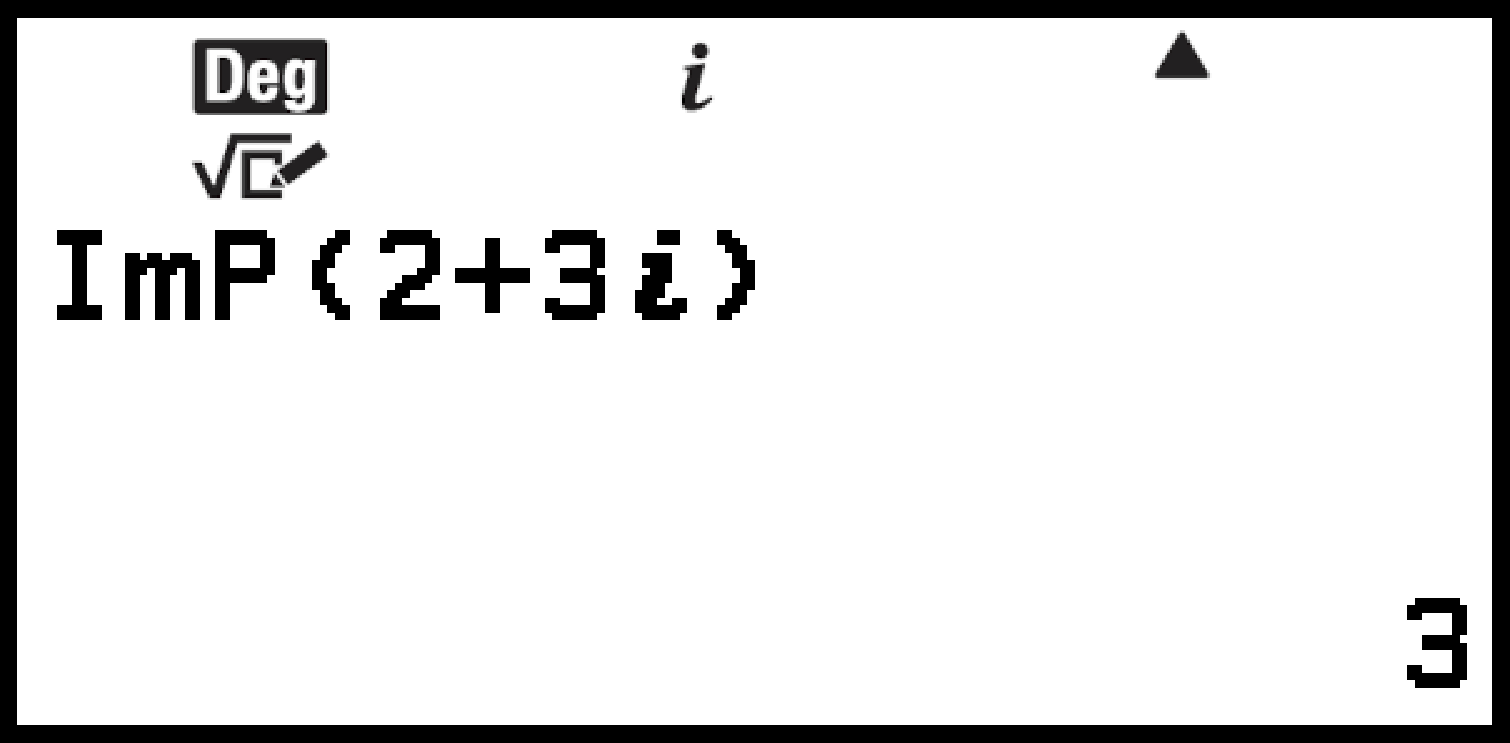
- – [Complexes] > [Partie imaginaire]
23(i) 
Conversion d’un résultat de calcul de nombre complexe en coordonnées rectangulaires ou polaires
Vous pouvez utiliser le menu FORMAT qui s’affiche lorsque vous appuyez sur 
pour convertir un résultat de calcul de nombre complexe en coordonnées rectangulaires ou polaires.
Exemple 9 : √2 + √2i = 2∠45, 2∠45 = √2 + √2i
(Unité d’angle : Degré, Forme complexe : a+bi)
- 22(i)
- – [Module, argument]
- – [Forme algébrique]
Utilisation de Vérification avec l’application Complexes
Après l’activation de Vérification dans l’application Complexes, vous pouvez déterminer si une égalité ou inégalité est vraie. Avec l’application Complexes, vous pouvez déterminer si une équation comprenant un nombre complexe est vraie ou fausse.
Note
Vérification peut être utilisé avec diverses applications de calculatrice. Avant d’effectuer les opérations de cette section, lisez d’abord les informations dans « Présentation de Vérification ».
Il est impossible de déterminer si une inégalité incluant un nombre complexe est vraie ou fausse (ERREUR maths).
Lorsque l’option Vérification est activée avec l’application Complexes, les éléments suivants sont les mêmes que ceux de l’application Calcul.
Exemple d’opération Vérification
Exemple 10 : Déterminer si i2 = -1 est vrai
1. Pour activer Vérification, appuyez sur 
, puis sélectionnez [Vérification ON].
Un indicateur 
s’affiche en haut de l’écran pour indiquer que Vérification est activé.
2. Saisissez i2 = -1 et déterminer si cela est vrai.
- (i)
– [Vérification] > [=] ((-))1 
3. Pour désactiver Vérification et quitter l’opération Vérification, appuyez sur , puis sélectionnez [Vérification OFF].
L’indicateur disparait de l’écran.
Pour plus d’informations à propos de la désactivation de Vérification, consultez « Pour désactiver Vérification ».
