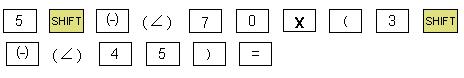Ja. Med följande modeller kan du enkelt hantera beräkningar med komplexa tal.
Modeller: fx-991MS/fx-115MS/fx-912MS/fx-3650P/fx-3950P
Sådana beräkningar, som ofta används i fysik- och tekniktillämpningar, förklaras här som komplement till räknarens användarhandbok.
Komplexa tal kan representeras i två olika former:
Rektangulär eller kartesisk form: z = x+iy (i en del notationer används j istället för i).
Polär form eller fasform: z = r∠θ eller z = |z|e^θi (i en del notationer används φ istället för θ).
Exempel 1: Konvertera det komplexa talet (z = -4+3i) till polär form.
1. Använd läget COMPLEX och ställ in vinkelenheten på Degree (grader) (Deg).
[MODE] [2](COMPLEX)
[MODE]...[1](Deg)
2. Mata in det komplexa talet z=-4+3i.
[(-)][4][+][3][ENG](i)[=]
3. Resultatet i kartesisk form.
Värdet för realdelen: -4
Värdet för den imaginära delen när du trycker på [SHIFT][=] (Re<->Im): 3 (i)
4. Visningsändringen av värdet i kartesisk form görs i polär form.
Absolutbeloppet av talet i polär form när du trycker på [SHFT][+](>r∠θ)[=]: 5
Argumentet när du trycker på [SHFT][=] (Re<->Im): 143.1301024
Resultatet i polär form: 5∠143.1301024 (vinkelenhet: Deg)
Exempel 2: Konvertera det komplexa talet (2∠60゜) till kartesisk form.
1. Använd läget COMPLEX och ställ in vinkelenheten på Degree (grader) (Deg).
[MODE] [2](COMPLEX)
[MODE]...[1](Deg)
2. Mata in det komplexa talet 2∠60.
[2][SHIFT][(-)](∠)[6][0][=]
3. Resultatet i kartesisk form.
Värdet för realdelen: 1
Värdet för den imaginära delen när du trycker på [SHIFT][=] (Re<->Im): 1.732050808 (i)
Resultatet i kartesisk form: 1+1.732050808i
Du kan även arbeta med vinkelenheten Radian (radianer). När vinkelenheten är Radian (radianer) kan du ange argumentvärden som multiplar av pi. (180゜ =π radianer.)
Exempel 2 ovan är beräknat i Radian (radianer).
1. Använd läget COMPLEX och ställ in vinkelenheten på Radian (radianer) (Rad).
[MODE][2](COMPLEX)
[MODE]...[2](Rad)
2. Mata in det komplexa talet 2∠π/3 (60゜ = π/3 radianer).
[2][SHIFT][(-)](∠)[SHIFT] [EXP](π)[ab/c] [3][=]
3. Resultatet i kartesisk form.
Värdet för realdelen: 1
Värdet för den imaginära delen när du trycker på [SHIFT][=] (Re<->Im): 1.732050808 (i)
Komplexa tal – Beräkning (addition/subtraktion)
De två komplexa talen z1 och z2 i kartesisk form är givna. :
z1 = 4+2i, z2 = -1+5i
Exempel 3: Addition z1+z2 = 3+7i
1. Använd läget COMPLEX och ställ in vinkelenheten på Degree (grader) (Deg).
[MODE] [2](COMPLEX)
[MODE]...[1](Deg)
2. Ange värdet. z1+z2. |
 |
Det resultat som visas:
Värdet för realdelen: 3
Värdet för den imaginära delen när du trycker på [SHIFT] [=] (Re<->Im): 7 (i)
Exempel 4: Subtraktion z1-z2 = 5-3i
1. Använd läget COMPLEX och ställ in vinkelenheten på Degree (grader) (Deg).
[MODE] [2](COMPLEX)
[MODE]...[1](Deg)
2. Ange värdet. z1-z2. |
 |
Det resultat som visas:
Värdet för realdelen: 5
Värdet för den imaginära delen när du trycker på [SHIFT] [=] (Re<->Im): -3 (i)
Komplexa tal – Beräkning (multiplikation/division)
De två komplexa talen z1 och z2 i polär form är givna - vinkelenheten är Degree (grader).
z1 =5∠70, z2 = 3∠45
Exempel 5: Multiplikation z1*z2 = 15∠115
1. Ange läget COMPLEX, ange polär form för visning av resultat från beräkningar med komplexa tal och ange vinkelenheten Degree (grader).
[MODE][2](COMPLEX)
[MODE]...[1](Disp)[höger pilknapp][2](r∠θ)
[MODE]...[1](Deg)
2. Ange värdet. z1*z2 |
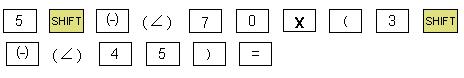 |
Det resultat som visas:
Absolutbeloppet av talet i polär form: 15
Argumentet när du trycker på [SHFT][=] (Re<->Im): 115
Exempel 6: Division z1/z2 = 1.666666667∠ 25
1. Ange läget COMPLEX, ange polär form för visning av resultat från beräkningar med komplexa tal och ange vinkelenheten Degree (grader).
[MODE][2](COMPLEX)
[MODE]...[1](Disp)[höger pilknapp][2](r∠θ)
[MODE]...[1](Deg)
2. Ange värdet. z1/z2 |
 |
Det resultat som visas:
Absolutbeloppet av talet i polär form: 1,666666667
Argumentet när du trycker på [SHFT][=] (Re<->Im): 25
3. Visningsändringen av värdet i polär form görs i kartesisk form.
Värdet för realdelen när du trycker på [SHIFT][-](>a+bi)[=]: 1.510512978
Värdet för den imaginära delen när du trycker på [SHIFT][=](Re<->Im): 0.704363769 (i) |