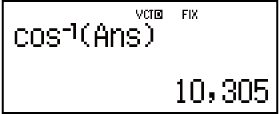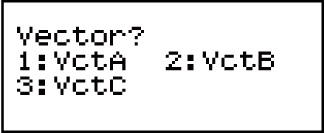Izibalo ze-Vector (VECTOR)

Sebenzisa Imodi ye-VECTOR ukwenza izibalo ze-vector ye-2-dimensional neye-3-dimensional. Ukwenza izibalo ze-vector, kufanele uqale ngokwabela idatha kuzimeleli ezikhethekile (VctA, VctB, VctC), bese usebenzisa izimeleli ezibalweni ezibonisiwe esibonelweni esingezansi.

Isibonelo 1: Ukwabela (1, 2) ku-VctA kanye (3, 4) ku-VctB, bese wenza izibalo ezilandelayo: (1, 2) + (3, 4)

1. Cindezela (VECTOR) ukufaka Imodi ye-VECTOR.

2. Cindezela (VctA)(2).

Lokhu kuzobonisa i-Vector Editor yokufaka i-vector ye-2-dimensional ye-VctA.

(1) "A" umele "VctA".

3. Faka amalungu e-VctA: 12.

4. Yenza izenzo ezilandelayo:
(VECTOR)(Data)(VctB)(2).

Lokhu kuzobonisa i-Vector Editor yokufaka i-vector ye-2-dimensional ye-VctB.

5. Faka amalungu e-VctB: 34.

6. Cindezela ukuthuthukisa isikrini sesibalo, nokwenza isibalo (VctA+VctB):
(VECTOR)(VctA)(VECTOR)(VctB).

Lokhu kuzobonisa isikrini se-VctAns esinemiphumela yesibalo.

(2) "Ans" umele "VctAns".

Phawula: "VctAns" umele "Vector Answer Memory". Bheka ethi "I-Vector Answer Memory" mayelana nokwaziswa okubanzi.

I-Vector Answer Memory

Noma nini lapho imiphumela yesibalo seyikhululiwe Kumodi ye-VECTOR eyi-vector, isikrini se-VctAns sizobonisa imiphumela. Imiphumela izokwabela nakusimeleli esibizwa "VctAns".
Isimeleli se-VctAns singasetshenziswa ezibalweni njengoba kuchaziwe ngezansi.

Ukufaka isimeleli se-VctAns esibalweni, yenza isenzo esilandelayo: (VECTOR)(VctAns).

Ukucindezela omunye walo khiye kuyilapho isikrini se-VctAns sibonisiwe kuzoshintshela esikrinini sesibalo ngokuzenzakalelayo: , , , . Isikrini sesibalo sizobonisa isimeleli se-VctAns esilandelwa ngesinye isenzo noma umsebenzi wokhiye ocindezelwe.

Ukwabela Nokuhlela Idatha Yesimeleli se-Vector

Kubalulekile!

Izenzo ezilandelayo azisekelwe yi-Vector Editor: , (M-), (STO). I-Pol, Rec, ÷R, nezitatimende ezikaningi ngeke zifakwe kanye ne-Vector Editor.

Ukwabela idatha entsha kokungaguquguquki kwe-vector:

1. Cindezela (VECTOR)(Dim), bese, kumenyu evelayo, ukhethe isimeleli se-vector ofuna ukwabela kuso idatha.

2. Kumenyu elandelayo evelayo, khetha ubukhulu (m).

3. Sebenzisa i-Vector Editor evelayo ukufaka izakhi ze-vector.

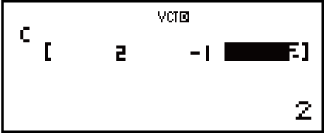
Isibonelo 2: Ukwabela (2, -1, 2) ku-VctC

(VECTOR)(Dim)(VctC)(3)
212

Ukushintsha amalungu okungaguquguqui kwe-vector:

1. Cindezela (VECTOR)(Data), bese, kumenyu evelayo, khetha isimeleli se-vector ofuna ukusihlela.

2. Sebenzisa i-Vector Editor evelayo ukuhlela izakhi ze-vector.
Hambisa i-cursor kuseli eliqukethe isakhi ofuna ukusishintsha, faka inani elisha, bese ucindezela .

Ukukopisha okuqukethwe kwesimeleli se-vector (noma i-VctAns):

1. Sebenzisa i-Vector Editor ukubonisa i-vector ofuna ukuyikopisha.

Uma ufuna ukukopisha i-VctA, ngokwesibonelo, sebenzisa okhiye abalandelayo: (VECTOR)(Data)(VctA).

Uma ufuna ukukopisha okuqukethwe kwe-VctAns, yenza lokhu okuboniswe esikrinini se-VctAns: (VECTOR)(VctAns).

2. Cindezela (STO), bese wenza esinye salezi zenzo zokhiye ukubalula indawo yokukopishela: (VctA), (VctB), noma (VctC).

Lokhu kuzobonisa i-Vector Editor enokuqukethwe kwendawo okukopishelwa kuyo.

Izibonelo Zezibolo ze-Vector

Izibonelo ezilandelayo zisebenzisa i-VctA = (1, 2) ne-VctB = (3, 4) Esibonelweni 1, ne-VctC = (2, -1, 2) Esibonelweni 2.

Isibonelo 3: 3 × VctA (I-Vector scalar multiplication), 3 × VctA - VctB (Isibonelo sesibalo kusetshenziswa i-VctAns)

3(VECTOR)(VctA)

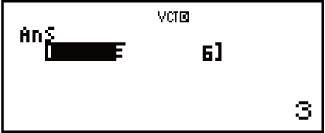
(VECTOR)(VctB)

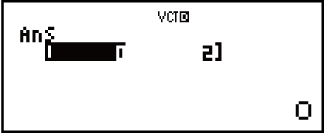
Isibonelo 4: VctA • VctB (Umphumela wechashazi we-Vector)

(VECTOR)(VctA)
(VECTOR)(Dot)
(VECTOR)(VctB)

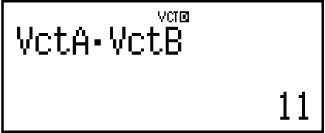
Isibonelo 5: VctA × VctB (Umphumela we-Vector cross)

(VECTOR)(VctA)
(VECTOR)(VctB)

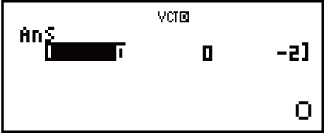
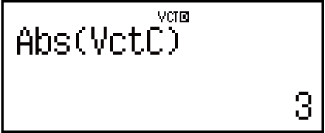
Isibonelo 6: Thola amanani aphelel e-VctC.

(Abs)
(VECTOR)(VctC)

Isibonelo 7: Nquma i-engele elenziwe nge-VctA ne-VctB ezinombolweni ezintathu ngemva kwekhoma (Fix 3). (Iyunithi ye-engele: Deg)

(cos𝜃 = ^{(𝐴∙𝐵)}_|𝐴||𝐵|, eba ngu 𝜃 = cos-1^{(𝐴∙𝐵)}_|𝐴||𝐵|)

(SETUP)(Fix)
(VECTOR)(VctA)
(VECTOR)(Dot)
(VECTOR)(VctB)
(Abs)(VECTOR)(VctA)
(Abs)(VECTOR)(VctB)

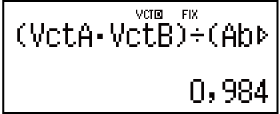
(cos-1)