Sebenzisa Imodi ye-MATRIX ukwenza izibalo ezihilela ama-matrix afikela emigqeni yamakholomu engu-3. Ukwenza isibalo se-matrix, kudingeka uqale ngokwabela idatha ezimelelini ezikhethekile ze-matrix (MatA, MatB, MatC), bese usebenzisa izimeleli esibalweni njengoba kubonisiwe esibonelweni esingezansi.

Isibonelo 1: Ukwabela i- ku-MatA ne- ku-MatB, bese wenza izibalo ezilandelayo: × (MatA×MatB), + (MatA+MatB)

1. Cindezela (MATRIX) ukufaka Imodi ye-MATRIX.

• 

2. Cindezela (MatA)(2×2).
Lokhu kuzobonisa i-Matrix Editor yokufaka izakhi ze-matrix ka-2 × 2 ozibalulile ye-MatA.

• 

• (1) "A" umele "MatA".

3. Faka izakhi ze-MatA: 2111.

4. Yenza izenzo ezilandelayo:
(MATRIX)(Data)(MatB)(2×2). Lokhu kuzobonisa i-Matrix Editor yokufaka izakhi ze-matrix ka-2 × 2 oyibalulile ye-MatB.

5. Faka izakhi ze-MatB: 2112.

6. Cindezela ukuthuthukisa isikrini sesibalo, futhi wenze isibalo sokuqala (MatA×MatB):
(MATRIX)(MatA)(MATRIX)(MatB).
Lokhu kuzobonisa isikrini se-MatAns esinemiphumela yesibalo.

(2) "Ans" umele "MatAns".

   Phawula: "MatAns" umele "Matrix Answer Memory". Bheka esithi "I-Matrix Answer Memory" mayelana nokwaziswa okubanzi.

7. Yenza isibalo esilandelayo (MatA+MatB):
(MATRIX)(MatA)(MATRIX)(MatB).

I-Matrix Answer Memory

Noma nini lapho imiphumela yesibalo ekhululiwe Kumodi ye-MATRIX iyi-matrix, isikrini se-MatAns sizovela nemiphumela. Imiphumela izokwabelwa isimeleli esithi "MatAns".
Isimeleli se-MatAns singasetshenziswa ezibalweni njengoba kuchaziwe ngezansi.

Ukufaka isimeleli se-MatAns esibalweni, sebenzisa okhiye abalandelayo: (MATRIX)(MatAns).

Ukucindezela noma yimuphi walabokhiye abalandelayo kuyilapho isikrini se-MatAns sibonisiwe kuzoshintsha ngokuzenzakalelayo esikrinini sokubala: , , , , , , (x3). Isikrini sesibalo sizobonisa isimeleli se-MatAns esilandelwa yisenzo noma umsebenzi wokhiye omcindezele.

Ukwabela Nokuhlela Idatha Yesimeleli se-Matrix

Ukwabela idatha entsha kokuguquguqukayo kwe-matrix:

1. Cindezela (MATRIX)(Dim), bese, kumenyu evelayo, ukhethe isimeleli se-matrix ofuna ukwabela kuso idatha.

2. Kumenyu elandelayo evelayo, khetha ubukhulu (m×n).

3. Khetha i-Metrix Editor evelayo ukufaka izakhi ze-matrix.

Isibonelo 2: Ukwabela i-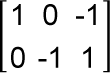 ku-MatC

• (MATRIX)
  (Dim)(MatC)(2×3)
  101011
• 

Ukushintsha amalungu okuguquguqukayo kwe-matrix:

1. Cindezela (MATRIX)(Data), bese, kumenyu evelayo, ukhethe isimeleli se-matrix ofuna ukusilungisa.

2. Sebenzisa i-Matrix Editor evelayo ukuhlela izakhi ze-matrix.
Hambisa i-cursor kuseli eliqukethe isakhi ofuna ukusishintsha, faka inani elisha, bese ucindezela .

Ukukopisha okuqukethwe kwesimeleli se-matrix (noma i-MatAns):

1. Sebenzisa i-Matrix Editor ukubonisa i-matrix ofuna ukuyikopisha.
Uma ufuna ukukopisha i-MatA, ngokwesibonelo, sebenzisa okhiye abalandelayo: (MATRIX)(Data)(MatA). Uma ufuna ukukopisha okuqukethwe kwe-MatAns, yenza okulandelayo ukubonisa isikrini se-MatAns: (MATRIX)(MatAns).

2. Cindezela (STO), bese wenza esinye salezi zenzo zokhiye ukubalula indawo yokukopishela: (MatA), (MatB), noma (MatC).
Lokhu kuzobonisa i-Matrix Editor ngokuqukethwe kwendawo yokukopishela.

Izibonelo Zezibalo Zemetriksi

Izibonelo ezilandelayo zisebenzisa i-MatA = ne-MatB = Esibonelweni 1, ne-MatC = 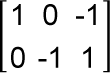Esibonelweni 2.

Isibonelo 3: 3 × MatA (i-Matrix Scalar Multiplication).

• 3(MATRIX)(MatA)
• 

Isibonelo 4: Thola isinqumi sika-MatA (det(MatA)).

• (MATRIX)(det)
  (MATRIX)(MatA)
• 1

Isibonelo 5: Thola ukudluliswa kuka-MatC (Trn(MatC)).

• (MATRIX)(Trn)
  (MATRIX)(MatC)
• 

Isibonelo 6: Thola okuphambene kwe-MatA (MatA-1).

Phawula: Ngeke ukwazi ukusebenzisa i- mayelana nalokhu okufakiwe. Sebenzisa lokhiye ukufaka i-"-1".

• (MATRIX)(MatA)
• 

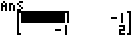
Isibonelo 7: Thola inani langempela lesakhi ngasinye se-MatB (Abs(MatB)).

• (Abs)(MATRIX)(MatB)
• 

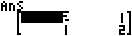
Isibonelo 8: Nquma i-square ne-cube le-MatA (MatA2, MatA3).

Phawula: Ngeke ukwazi ukusebenzisa i- mayelana nalokhu okufakiwe. Sebenzisa i- ukubalula i-squaring, kanye ne-(x3) ukubalula i-cubing.

• (MATRIX)(MatA)
• 

• (MATRIX)(MatA)(x3)
• 

Isibonelo 9: Nquma i-MatA = ifomu lomugqa we-echelon.

• (MATRIX)(Ref)
  (MATRIX)(MatA)
• 

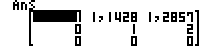
Isibonelo 10: Nquma i-MatA = ifomu elincishisiwe lomugqa we-echelon.

• (MATRIX)(Rref)
  (MATRIX)(MatA)
•