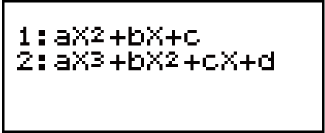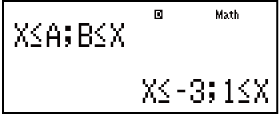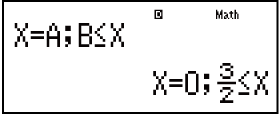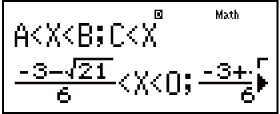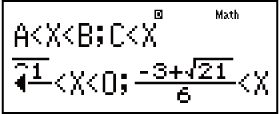Izibalo Zokungalingani (INEQ)
Ungasebenzisa inqubo elandelayo ukuxazulula ukungalingani oku-quadratic noma oku-cubic.
1. Cindezela 
(INEQ) ukufaka Imodi ye-INEQ.
2. Kumenyu evelayo, khetha uhlobo lokungalingani.
| Ukukhetha uhlobo lokungalingani: | Cindezela lo khiye: |
|---|---|
| Ukungalingani kwe-quadratic |  (aX2 + bX + c) |
| Ukungalingani kwe-cubic | (aX3 + bX2 + cX + d) |
3. Kumenyu evelayo, sebenzisa lo khiye ukuya kulo 
ukukhetha uhlobo lophawu lokungalingani ne-oriantation.
4. Sebenzisa i-kuKho-efishiyenti Editha evelayo ukufaka izimeleli ze-coefficient.
Ukuxazulula u-x2 + 2x - 3 < 0, ngokwesibonelo, faka ama-coefficient ka-a = 1, b = 2, c = -3 ngokucindezela u-1
2
3.
Ukuze ushintshe inani elifanelekile osunakho ukufaka, hambisa isikhombisi kuseli elifanele, ufake inani elisha, bese ucindezela u-.
Ukucindezela u-
kuzosula wonke ama-coefficients abe yi-zero.
Phawula: Imisebenzi elandelayo ayisekelwa yiKho-efishiyenti Editha: 
, 
(M-), 
(STO). I-Pol, i-Rec, ÷ R, kanye nezitatimende ezixubile nazo azikwazi ukufakwa kuKho-efishiyenti Editha.
5. Ngemuva kokuthi onke amanani ayindlela ofuna ngayo, cindezela u-.
Lokhu kuzobonisa izisombululo.
Ukuze uphindele ku-kuKho-efishiyenti Editha kuyilapho izisombululo ziboniswe esikrinini, cindezela .
Phawula
Amanani ngeke aguqulelwe ku-engineering notation esikrinini sesisombululo.
Ukushintsha Uhlobo Lokungalingani
Cindezela (INEQ) bese ukhetha uhlobo lokungalingani kumenyu evelayo. Ukushintsha uhlobo lokungalingani kubangela amanani wawo wonke ama-coefficient we-kuKho-efishiyenti Editha ukushintshela eqandeni.
Izibonelo Zesibalo Semodi ye-INEQ
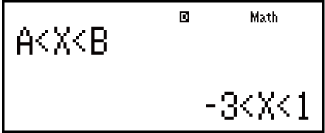
Isibonelo 1: x2 + 2x - 3 < 0 (MthIO-MathO)
- (INEQ)(aX2 + bX + c)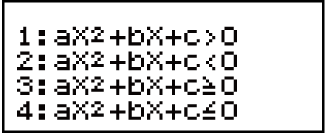
- (aX2 + bX + c < 0)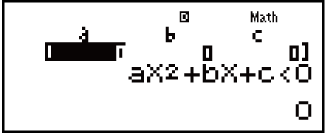
- 123
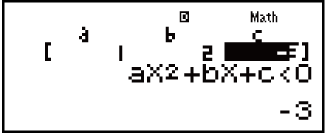
Isibonelo 2: x2 + 2x - 3 ≧ 0 (MthIO-MathO)
- (INEQ)(aX2 + bX + c)
(aX2 + bX + c ≧ 0)
123 
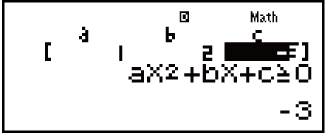
- Phawula: Izisombululo ezibonisiwe njengoba kuveziwe lapha uma Isibonisi Somugqa sikhethiwe
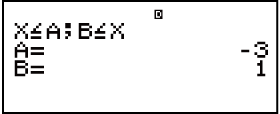
Isibonelo 3: 2x3 - 3x2 ≧ 0 (MthIO-MathO)
- (INEQ)(aX3 + bX2 + cX + d)
(aX3 + bX2 + cX + d ≧ 0)
23 
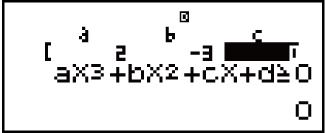
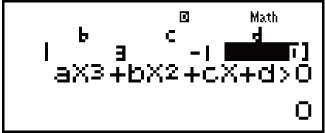
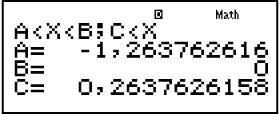
Isibonelo 4: 3x3 + 3x2 - x > 0 (MthIO-MathO)
- (INEQ)(aX3 + bX2 + cX + d)
(aX3 + bX2 + cX + d > 0)
331 
- Phawula: Izisombululo ezibonisiwe njengoba kuveziwe lapha uma Isibonisi Somugqa sikhethiwe.
Isibonisi Sesisombululo Esikhethekile
Ethi "All Real Numbers" ivela esikrinini uma kunesisombululo sokungalingani kwazo zonke izinombolo.
Isibonelo: x2 ≧ 0 (MthIO-MathO)
- (INEQ)(aX2 + bX + c)
(aX2 + bX + c ≧ 0)
100 
Ethi "No-Solution" ivela esikrinini sesisombululo uma kungekho sisombululo esiphumayo kokungalingani (njengo-X2 < 0).
