Izibalo Zokwaba (DIST)
Ungasebenzisa izinqubo ngezansi ukwenza iinhlobo eziyisikhombisa ezihlukahlukene zezibalo zokusabalalisa.
1. Cindezela 

 (DIST) ukufaka Imodi ye-DIST.
(DIST) ukufaka Imodi ye-DIST.
2. Kumenyu evelayo, khetha uhlobo lwesibalo sokusabalalisa.
| Ukukhetha lolu hlobo lwesibalo: | Cindezela lo khiye: |
|---|---|
| I-Norrmal probability density |  (Normal PD) (Normal PD) |
| I-Normal cumulative distribution |  (Normal CD) (Normal CD) |
| I-Inverse normal cumulative distribution |  (Inverse Normal) (Inverse Normal) |
| I-Binomial probability |  (Binomial PD) (Binomial PD) |
| I-Binomial cumulative distribution |   (Binomial CD) (Binomial CD) |
| I-Poisson probability |   (Poisson PD) (Poisson PD) |
| I-Poisson cumulative distribution |   (Poisson CD) (Poisson CD) |
3. Ukufaka amanani wezimeleli.
Nge-Binomial PD, Binomial CD, Poisson PD, ne-Poisson CD, ungafaka isampula ledatha bese wenza izibalo.
4. Emuva kokufaka amanani wazo zonke izimeleli, cindezela  .
.
Lokhu kuveza imiphumela yesibalo.
Ukucindezela i- noma i-
noma i- kuyilapho imiphumela ibonisiwe kuzobuyisela okufakiwe esikrinini sesimeleli sokuqala.
kuyilapho imiphumela ibonisiwe kuzobuyisela okufakiwe esikrinini sesimeleli sokuqala.
Phawula
Ukushintsha uhlobo lwesibalo sokusabalalisa emva kokufaka Imodi ye-DIST, cindezela 
 (STAT/DIST)
(STAT/DIST) (Type) bese ukhetha uhlobo lwesisabalalisi osifunayo.
(Type) bese ukhetha uhlobo lwesisabalalisi osifunayo.
Ukunemba kwesibalo sokusabalalisa kufinyelela kumadijithi amahlanu aphawulekayo.
Izimeleli Ezamukela Okufakwayo
Izimeleli ezilandelayo zesibalo sokusabalalisi ezamukela ukufakwa kwamanani.
I-Normal PD ........................... x, σ, μ
I-Normal CD ........................... I-Lower , I-Upper, σ, μ
I-Inverse Normal .................... I-Area, σ, μ (Isethingi le-Tail njalo ngakwesokudla.)
I-Binomial PD, I-Binomial CD ... x (noma List), N, p
I-Poisson PD, I-Poisson CD ..... x (noma List), μ
x: data
σ: i-standard deviation (σ < 0)
μ: i-mean
I-Lower: i-lower boundary
I-Upper: i-upper boundary
I-Tail: inani lamathuba e-tail.
I-Area: inani lamathuba (0 ≦ Area ≦ 1)
I-List: i-list yesampula yedatha
N: inani lemizamo
p: impumelelo yethuba (0 ≦ p ≦ 1)
I-List Lwesikrini (Binomial PD, Binomial CD, Poisson PD, Poisson CD)
Nge-Binomial PD, Binomial CD, Poisson PD, ne-Poisson CD, sebenzisa Isikrini se-List sesampula yedatha yokufakwayo. Ungafaka amasampula edatha angafika ku-25 ngokuguquguqukayo ngakunye. Imiphumela yokubala ibonisiwe Esikrinini se-List.
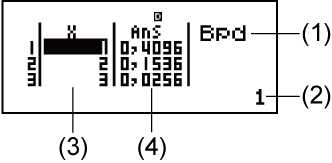 (1) Uhlobo lwesibalo sokusabalalisa
(1) Uhlobo lwesibalo sokusabalalisa
(2) Inani elisendaweni yamanje ye-cursor
(3) X: Isampula yedatha
(4) Ans: Imiphumela yesibalo
Ukuhlela isampula yedatha:
Hambisa i-cursor kuseli eliqukethe idatha ofuna ukuyihlela, ufake idatha entsha, bese ucindezela  .
.
Ukususa yonke idatha:
Hambisa i-cursor iye kusampula yedatha ofuna ukuyisusa bese ucindezela  .
.
Ukufaka isampula yedatha:
Hambisa i-cursor endaweni lapho ofuna ukuufaka khona isampula yedatha, cindezela 
 (STAT/DIST)
(STAT/DIST) (Edit)
(Edit) (Ins), bese ufaka isampula yedatha.
(Ins), bese ufaka isampula yedatha.
Ukususa yonke isampula yedatha:
Cindezela 
 (STAT/DIST)
(STAT/DIST) (Edit)
(Edit) (Del-A).
(Del-A).
Izibonelo Zesibalo Semodi ye-DIST
Isibonelo 1: Ukubala amathuba okuminyana okujwayelekile okungenzeka uma u-x = 36, σ = 2, μ = 35


 (DIST)
(DIST)
 (Normal PD)
(Normal PD)
- 36


- 2


- 35

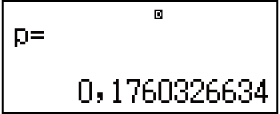
Imiphumela: 0,1760326634
Ukucindezela i- noma i-
noma i- kuphindela esikrinini sokufaka u-x.
kuphindela esikrinini sokufaka u-x.
Isibonelo 2: Ukubala amathuba e-binomial yesampula yedatha {10; 11; 12; 13; 14} uma u-N = 15 no-p = 0,6


 (DIST)
(DIST) (Binomial PD)
(Binomial PD)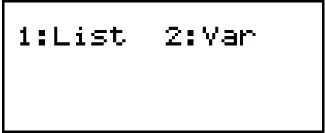
- Bonisa Isikrini se-List:
 (List)
(List) 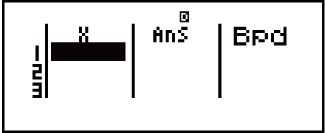
Ukubalula idatha usebenzisa ifomethi yepharamitha, cindezela  (Var).
(Var).
- 10
 11
11 12
12 13
13 14
14
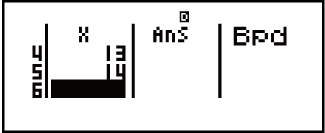
- 15


- 0
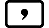 6
6
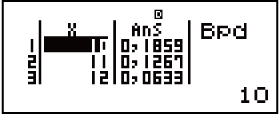
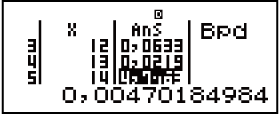
Imiphumela:x = amathuba we-binomial ka-10 ≒ 0,18594
x = amathuba we-binomial ka-11 ≒ 0,12678
x = amathuba we-binomial ka-12 ≒ 0,063388
x = amathuba we-binomial ka-13 ≒ 0,021942
x = amathuba we-binomial ka-14 ≒ 4,7018 × 10-3
Ukucindezela i- kuphindela esikrinini sokufaka i-N. Ukucindezela i-
kuphindela esikrinini sokufaka i-N. Ukucindezela i- kuphindela Esikrini se-List (ukufaka amasampula edatha elondiwe).
kuphindela Esikrini se-List (ukufaka amasampula edatha elondiwe).
Phawula
Okulandelayo ngeke kusetshenziswe ekusabalaliseni izibalo: Pol, Rec, ÷R, ∫, d/dx.
Uma idatha ibaluliwe kusetshenziswa ifomethi yepharamitha, bala imiphumela elondwe enkumbulweni ye-Ans.
Umyalezo wephutha uyavela uma inani elifakiwe lingaphandle komahluko ovumelekile. Okuthi "ERROR" kuzovela kukholomu le-Ans Esikrinini se-List uma inani elifakiwe lesampula yedatha ehambisanayo lingaphandle komahluko ovumelekile.