Izibalo Zezinombolo Eziphicayo (CMPLX)

Ukwenza izibalo zezinombolo eziyinkimbinkimbi, qala ngokucindezela (CMPLX) ukuze ufake Imodi ye-CMPLX.

Ungasebenzisa noma yizixhumanisi zesikwele eside (a+bi) noma izixhumanisi ze-polar (r∠θ) ukufaka izinombolo eziyinkimbinkimbi.
Imiphumela yezibalo zezinombolo eziyinkimbinkimbi iboniswe ngokuvumelana nefomethi yesethingi lenani eliyinkimbinkimbi kumenyu yokusetha.

Isibonelo 1: (2 + 6i) ÷ (2i) = 3 - i (Ifomethi yenombolo eyinkimbinkimbi: a+bi)

26(i)2(i)
3-i

Isibonelo 2: 2∠45 = √2 + √2i (MthIO-MathO) (Iyunithi ye-engele: Deg)

(Ifomethi yenombolo eyinkimbinkimbi: a+bi)

2(∠) 45
√2+√2i

Isibonelo 3: √2 + √2i = 2∠45 (MthIO-MathO) (Iyunithi ye-engele: Deg)

(Ifomethi yenombolo eyinkimbinkimbi: r∠θ)

22(i)
2∠45

Phawula

Uma uhlela ukwenza okufakwayo kanye nokuboniswa kwemiphumela yesibalo ngokwefomethi yezixhumanisi ze-polar, balula iyunithi ye-engele ngaphambi kokuqalisa isibalo.

Inani lika-θ emphumeleni wesibalo libonisiwe mahlukweni walokhu, -180° < θ ≦ 180°.

Ukubonisa imiphumela yesibalo kuyilapho Isibonisi Somugqa sikhethiwe kuzobonisa i-a ne-bi (noma r ne-θ) emigqeni ehlukene.

Izibonelo Zesibalo se-CMPLX Mode

Isibonelo 1: (1 - i)-1 = ¹₂ + ¹₂i (MthIO-MathO) (Ifomethi yenombolo eyinkimbinkimbi: a+bi)

1(i)
¹₂+¹₂i

Isibonelo 2: (1 + i)2 + (1 - i)2 = 0 (MthIO-MathO)

1(i)1(i)
0

Isibonelo 3: Ukuze uthole i-conjugate yenombolo eyinkimbinkimbi ka-2 + 3i

(Ifomethi yenombolo eyinkimbinkimbi: a+bi)

(CMPLX)(Conjg) 23(i)
2-3i

Isibonelo 4: Ukuze uthole inani langempela lempikiswano ka-1 + i (MthIO-MathO) (Iyunithi ye-engele: Deg)

Inani Langempela (Abs):

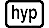(Abs) 1(i)
√2

Impikiswano (arg):

(CMPLX)(arg) 1(i)
45

Ukusebenzisa Isiqondisi Sefomethi Yokubalula Imiphumela Yesibalo

Esinye salezi ziqondisi ezimbili ezikhethekile (r∠θ noma a+bi) singafakwa ekugcineni kwesibalo ukubalula ifomethi yesibonisi semiphumela yesibalo.
Isiqondisi simisela phezu kwefomethi yesethingi lenombolo eyinkimbinkimbi yomshini wokubala.