Ukusebenzisa i-SOLVE
I-SOLVE isebenzisa indlela kaNewton yokuhlawumbisela isixazululo sama-equation.
Phawula ukuthi i-SOLVE ingasetshenziswa kuyi-COMP Mode kuphela.
Okulandelayo kuchaza izinhlobo zezibalo izisombululo zazo ezingatholwa kusetshenziswa i-SOLVE.
Izibalo ezinesimeleli u-X: X2 + 2X - 2, Y = X + 5, X = sin(M), X + 3 = B + C
i-SOLVE ixazulula u-X. Isichazi esinjengo-X2 + 2X - 2 siphathwa njengo-X2 + 2X - 2 = 0.
Ukufakwa kwezibalo usebenzisa i-syntax elandelayo: {isibalo}, {isisombululo sesimeleli}
i-SOLVE ixazulula u-Y, ngokwesibonelo, uma isibalo sifakwe njengalokhu: Y = X + 5, Y
Kubalulekile!
Uma isibalo siqukethe okufakwayo kokusebenza okuhilela abakaki abavulayo (njengo-sin no-log), ungabasusi abakaki abavalayo.
Imisebenzi elandelayo ayivunyelwanga ngaphakathi kwesibalo: ∫, d/dx, Σ, Pol, Rec, ÷R.
Isibonelo: Ukuxazulula u-y = ax2 + b ngokuka-x lapho u-y = 0, a = 1, no-b = -2
 (Y)
(Y)
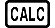 (=)
(=)
 (A)
(A)
 (X)
(X)

 (B)
(B)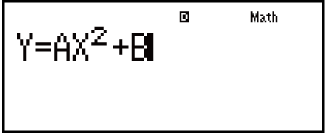

 (SOLVE)
(SOLVE)
-
(1) Iziqondisi zokufaka inani lika-Y
(2) Inani lamanje lika-Y
- 0
 1
1
 2
2
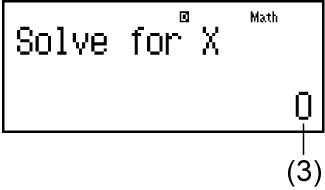
-
(3) Inani lamanje lika-X
Faka inani lokuqala lika-X (Lapha, faka u-1):
- 1

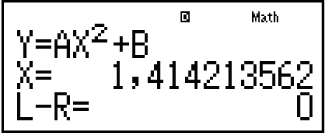
Isikrini Sesisombululo
- Ukuphuma ku-SOLVE:

Phawula
Phakathi nesikhathi lapho ucindezela u-
 (SOLVE) uze uphume ku-SOLVE ngokucindezela ku-
(SOLVE) uze uphume ku-SOLVE ngokucindezela ku- , kufanele usebenzise izinqubo zokufaka Isibonisi Somugqa mayelana nokufaka.
, kufanele usebenzise izinqubo zokufaka Isibonisi Somugqa mayelana nokufaka.
Kubalulekile!
Kuye ngokuthi ufaka ini ngokuqondene nenani lika-X (inani lesisombululo), i-SOLVE kungenzeka ingakwazi ukuthola izisombululo. Uma lokhu kwenzeka, zama ukushintsha inani lokuqala ukuze libe seduze nesisombululo.
I-SOLVE kungenzeka ingakwazi ukunquma isisombululo esifanele, ngisho nalapho kunesisodwa.
I-SOLVE isebenzisa indlela ka-Newton, ngakho uma kunezisombululo eziningi, kuzobuyiswa esisodwa sazo kuphela.
Ngenxa yokulinganiselwa kwendlela ka-Newton, izisombululo kuvame ukuba nzima ukuzithola ezibalweni ezinjengalesi esilandelayo: y = sin(x), y = ex, y = √x.
Okuqukethwe Yisikrini Sezisombululo
Izisombululo zihlala ziboniswe ngokwendlela yedesimali.

(1) Isibalo (Isibalo osifakayo.)
(2) Isimeleli esixazululiwe se-
(3) Isisombululo
(4) Umphumela (Ohlangothini Lwesobunxele) - (Ohlangothini Lwesokudla)
"Umphumela (Ohlangothini Lwesobunxele) - (Ohlangothini Lwesokudla)" ubonisa imiphumela lapho uhlangothi lwesokudla lwesibalo lukhishiwe ohlangothini lwesobunxele, ngemuva kokwabela inani elitholiwe kusimeleli esixazululwayo. Njengoba lo mphumela usondela kokuyiqanda, yilapho kuba ukunemba kwesisombululo.
Isikrini Sokuqhubeka
I-SOLVE yenza ukuguqulela izikhathi ezimbalwa kusengaphambili. Uma kungenakuthola isisombululo, kubonisa isiqinisekiso esikrinini esikhombisa okuthi "Continue: [=]", esikubuza ukuthi uyafuna ukuqhubeka yini.
Cindezela  ukuze uqhubeke noma
ukuze uqhubeke noma  ukuze ukhansele isenzo se-SOLVE.
ukuze ukhansele isenzo se-SOLVE.
Isibonelo: Ukuxazulula y = x2 - x + 1 ngokuka-x lapho u-y = 3, 7, no-13.
 (Y)
(Y)
 (=)
(=)
 (X)
(X)

 (X)
(X) 1
1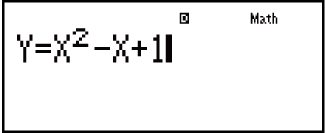

 (SOLVE)
(SOLVE)
- 3

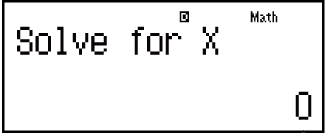
Faka inani lokuqala lika-X (Lapha, faka u-1):
- 1

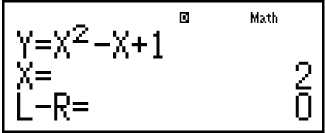
 7
7

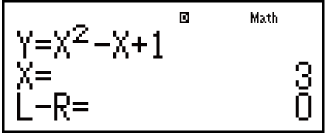
 13
13