Ukushintshashintsha Imiphumela Yokubala
Njengoba Isibonisi Semvelo sikhethiwe, ukucindezela ngakunye kwe-
kuzoguquguqula imiphumela yesibalo esibonisiwe phakathi nesimo saso sefrakshini nesimo sedesimali, isimo saso se-√ nesimo sedesimali, noma isimo saso se-π nesimo saso sedesimali.
Isibonelo 1: π ÷ 6 = 16 π = 0,5235987756 (MthIO-MathO)
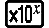(π)
6
- 16 π
0,5235987756
Isibonelo 2: (√2 + 2) × √3 = √6 + 2√3 = 5,913591358 (MthIO-MathO)
2
2
3- √6 + 2√3 5,913591358
Njengoba Isibonisi Somugqa sikhethiwe, ukucindezela ngakunye kwe- uzoguquguqula imiphumela yesibalo esibonisiwe phakathi nesimo saso sedesimali nesimo sefrakshini.
Isibonelo 3: 1 ÷ 5 = 0,2 = 15 (LineIO)
- 15
- 0,2 1
5
Isibonelo 4: 1 - 45 = 15 = 0,2 (LineIO)
- 1
4
5 - 15 0,2
Kubalulekile!
Kuye ngohlobo lomphumela wesibalo esiboniswayo lapho ucindezela lo khiye , inqubo yokuguqulela ingathatha isikhashana ukwenzeka.
Ngemiphumela ethile yesibalo, ukucindezela lo khiye ngeke kuguqule inani elibonisiwe.
Ngeke ukwazi ukushintshela isimo sedesimali kwesefrakshini exutshiwe uma inani eliphelele lamadijithi asetjenzisiwe kufrakshini exutshiwe (okuhlanganisa inombolo ephelele, inombolo engaphezulu, inombolo engaphansi, nezimpawu zokuhlukanisa) lingaphezu kuka-10.
Phawula
Ngesibonisi Semvelo (MathO), ukufaka esinye salezi zibalo ezilandelayo bese ucindezela esikhundleni se- kuzobonisa umphumela wesibalo ngokwesimo sedesimali: isibalo esiphumela esimweni se-√ noma esimweni se-π, isibalo sesihlukanisi. Ukucindezela emva kwalokho kuzoshintshela esimweni sefrakshini noma esimweni se-π somphumela wesibalo. Isimo somphumela we-√ ngeke sivele kulokhu.
