Ukulandelana Kokubaluleka Kwesibalo
Ukulandelana kokubaluleka kwesibalo esifakiwe kuhlaziywa ngokuvumelana nemithetho engezansi.
Uma ukubaluleka kwezibalo ezimbili kulingana, isibalo senziwa kusuka kwesobunxele kuya kwesokudla.
| 1 | Izibalo ezikubakaki |
|---|---|
| 2 | Amafankshini adinga i-argument eya ngakwesokudla nomkaki ovalayo ")" ngemva kwe-argument |
| 3 | Imisebenzi eza ngemva kokufaka inani (x2, x3, x-1, x!, °’ ”, °, r, g, %), ama-power (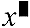 ), ama-root ( ), ama-root (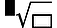 ) ) |
| 4 | Amaqhezu |
| 5 | Uphawu lokususa ((-)), izimpawu ze-base-n (d, h, b, o) |
| 6 | Imodi ye-STAT yenani elisikiselwe (xˆ, yˆ, xˆ1, xˆ2) |
| 7 | Ukuphindaphinda lapho uphawu lokuphindaphinda lweqiwe |
| 8 | Ukubala (nPr), inhlanganisela (nCr) |
| 9 | Ukuphindaphinda (×), ukuhlukanisa (÷), ukubalwa kokusele (÷R) |
| 10 | Ukuhlanganisa (+), ukususa (-) |
| 11 | and (insizakubala enelojiki) |
| 12 | or, xor, xnor (izinsizakubala ezinelojiki) |
Phawula
Uma uphindaphinda inani elinophawu lokususa (njengo -2), inani eliphindaphindwayo kumelwe livalelwe kubakaki (
 2
2

 ). Njengoba u-x2 esezingeni eliphakeme kunophawu lokususa, ukufaka u-
). Njengoba u-x2 esezingeni eliphakeme kunophawu lokususa, ukufaka u- 2
2
 kuzobangela umphumela wesikwele sika-2 bese kunezela uphawu lokususa emphumeleni.
kuzobangela umphumela wesikwele sika-2 bese kunezela uphawu lokususa emphumeleni.
Njalo gcina ukulandelana kuvelele engqondweni, futhi uvalele amanani anophawu lokususa kubaki uma kudingeka.

