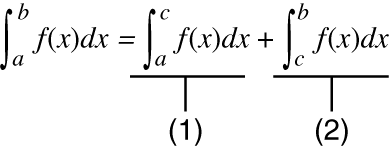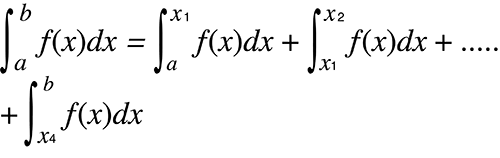Cálculos de integração
Função para realizar integração numérica utilizando o método Gauss-Kronrod.
A sintaxe para inserção da Exibição Natural é ∫ba f (x)dx, enquanto a sintaxe para inserção da Exibição Linear é ∫ (f (x), a, b, tol).
tol especifica a tolerância, que se torna 1 × 10-5 quando nada é inserido para tol.
Exemplo 1: ∫e1 ln(x) = 1
(MthIO-MathO)
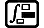

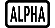
 (X)
(X)
 1
1
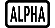
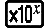 (e)
(e)
- 1
(LineIO)

 (X)
(X)
 (,) 1
(,) 1
 (,)
(,)
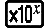 (e)
(e)

- 1
Exemplo 2: ∫(1x2 , 1, 5, 1 × 10-7) = 0,8 (LineIO)
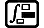 1
1
 (X)
(X)
 (,) 1
(,) 1
 (,) 5
(,) 5
 (,)
(,)
1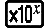
 7
7

- 0,8
Exemplo 3: ∫π0 (sin x + cos x)2 dx = π (tol: não especificada) (MthIO-MathO) (unidade de ângulo: Rad)
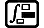


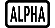
 (X)
(X)


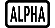
 (X)
(X)


 0
0
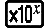 (π)
(π)
- π
Precauções de cálculo de integração
O cálculo de integração só pode ser efetuado no modo COMP.
Os cálculos a seguir não podem ser utilizados em f(x), a, b ou tol: Pol, Rec, ∫, d/dx, Σ.
Ao utilizar uma função trigonométrica em f(x), especifique Rad como a unidade de ângulo.
Um valor tol menor aumenta a precisão, mas também aumenta o tempo de cálculo. Ao especificar tol, utilize valores como 1 × 10-14 ou superiores.
A integração normalmente exige muito tempo para ser efetuada.
Dependendo do conteúdo de f(x) e da área de integração, podem ser gerados erros de cálculos que ultrapassam a tolerância, fazendo com que a calculadora exiba uma mensagem de erro.
O conteúdo de f(x), valores positivos/negativos dentro do intervalo de integração, e o intervalo a ser integrado podem causar um erro grande nos valores de integração resultantes. (Exemplos: quando há partes com pontos descontínuos ou alteração abrupta; quando o intervalo de integração é muito amplo.) Em tais casos, dividir o intervalo de integração em partes para efetuar o cálculo pode melhorar a precisão do cálculo.
Dicas para cálculos de integração bem-sucedidos
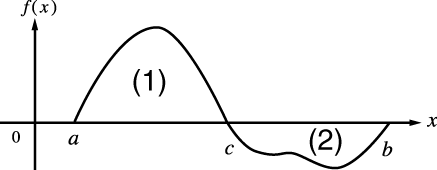
Quando uma função periódica ou intervalo de integração resultar em valores de função f(x) positivos e negativos
Efetue integrações diferentes para cada ciclo ou para as partes negativa e positiva e, em seguida, combine os resultados.
(1) Parte positiva
(2) Parte negativa
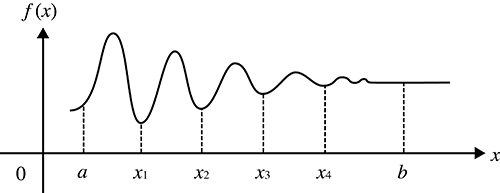
Quando os valores de integração oscilam muito devido às mudanças de minuto no intervalo de integração
Divida o intervalo de integração em múltiplas partes (de modo que divida as áreas de oscilação amplas em partes pequenas), efetue a integração em cada parte e, em seguida, combine os resultados.