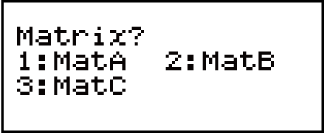CASIO

Gebruik die MATRIX-modus om berekeninge uit te voer wat matrikse van tot 3 rye by 3 kolomme behels. Om 'n matriksberekening uit te voer, ken eers data aan spesiale matriksveranderlikes (MatA, MatB, MatC) toe en gebruik dan die veranderlikes in die berekening soos vertoon in die voorbeeld hier onder.

Voorbeeld 1: Om aan MatA en  aan MatB toe te ken, en daarna die volgende berekeninge uit te voer: × (MatA×MatB), + (MatA+MatB)

1. Druk (MATRIX) om na die MATRIX-modus te verander.

• 

2. Druk (MatA)(2×2).
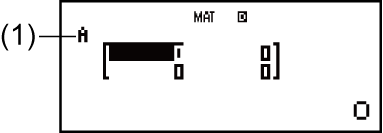
Dit sal die matriksredigeerder vertoon waarin die elemente van die 2 × 2-matriks wat vir MatA gespesifiseer is, ingesleutel moet word.

• 

• (1) "A" staan vir "MatA".

3. Sleutel die elemente van MatA in: 2111.

4. Voer die volgende insleuteling uit:
(MATRIX)(Data)(MatB)(2×2). Dit sal die matriksredigeerder vertoon waarin die elemente van die 2 × 2-matriks wat vir MatB gespesifiseer is, ingesleutel moet word.

5. Sleutel die elemente van MatB in: 2112.

6. Druk om na die berekeningskerm te gaan, en voer die eerste berekening uit (MatA×MatB):
(MATRIX)(MatA)(MATRIX)(MatB).
Dit sal die MatAns-skerm met die berekeningsresultate vertoon.

(2) "Ans" staan vir "MatAns".

   Neem kennis: "MatAns" staan vir "Matrix Answer Memory". Kyk "Matrix-antwoordgeheue" vir meer inligting.

7. Voer die volgende berekening uit (MatA+MatB):
(MATRIX)(MatA)(MATRIX)(MatB).

Matriks-antwoordgeheue

Wanneer die resultaat van 'n berekening wat in die MATRIX-modus uitgevoer is, 'n matriks is, sal die MatAns-skerm die resultaat vertoon. Die resultaat sal ook aan 'n veranderlike genaamd "MatAns" toegeken word.
Die MatAns-veranderlike in berekeninge kan gebruik word soos hier onder beskryf.

Om die MatAns-veranderlike in 'n berekening in te voeg, voer die volgende insleuteling uit: (MATRIX)(MatAns).

Om enige van die volgende sleutels te druk terwyl die MatAns-skerm vertoon word, sal outomaties na die berekeningskerm oorskakel: , , , , , , (x3). Die berekeningskerm sal die MatAns-veranderlike vertoon, gevolg deur die operateur of funksie vir die sleutel wat gedruk is.

Om matriksveranderlike-data toe te ken en te redigeer

Om nuwe data aan 'n matriksveranderlike toe te ken:

1. Druk (MATRIX)(Dim) en selekteer dan op die keuselys wat verskyn die matriksveranderlike waaraan data toegeken moet word.

2. Op die volgende keuselys wat verskyn, selekteer afmeting (m×n).

3. Gebruik die matriksredigeerder wat verskyn om die elemente van die matriks in te sleutel.

Voorbeeld 2: Om 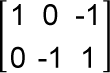aan MatC toe te ken

• (MATRIX)
  (Dim)(MatC)(2×3)
  101011
• 

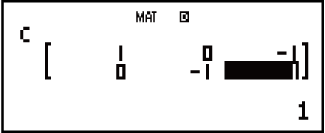
Om die elemente van 'n matriksveranderlike te verander:

1. Druk (MATRIX)(Data) en selekteer dan op die keuselys wat verskyn die matriksveranderlike wat geredigeer moet word.

2. Gebruik die matriksredigeerder wat verskyn om die elemente van die matriks te redigeer.
Beweeg die wyser na die sel wat die element bevat wat verander moet word, sleutel die nuwe waarde in, en druk dan .

Om matriksveranderlike- (of MatAns) inhoud te kopieer:

1. Gebruik die matriksredigeerder om die matriks wat gekopieer moet word, te vertoon.
Indien MatA byvoorbeeld gekopieer moet word, voer die volgende insleuteling uit: (MATRIX)(Data)(MatA). Indien die MatAns-inhoud gekopieer moet word, voer die volgende uit om die MatAns-skerm te vertoon: (MATRIX)(MatAns).

2. Druk (STO) en voer dan een van die volgende insleutelings uit om die kopieerbestemming te spesifiseer: (MatA), (MatB), of (MatC).
Dit sal die matriksredigeerder met die inhoud van die kopieerbestemming vertoon.

Matriksberekeningsvoorbeelde

Die volgende voorbeelde gebruik MatA = , MatB = uit Voorbeeld 1, en MatC = 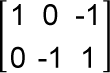uit Voorbeeld 2.

Voorbeeld 3: 3 × MatA (matriks-skalaarvermenigvuldiging).

• 3(MATRIX)(MatA)
• 

Voorbeeld 4: Om die determinant van MatA te verkry (det(MatA)).

• (MATRIX)(det)
  (MATRIX)(MatA)
• 1

Voorbeeld 5: Om die transposisie van MatC te verkry (Trn(MatC)).

• (MATRIX)(Trn)
  (MATRIX)(MatC)
• 

Voorbeeld 6: Om die inverse matriks van MatA te verkry (MatA-1).

Neem kennis: kan nie vir hierdie insleuteling gebruik word nie. Gebruik die -sleutel om "-1" in te sleutel.

• (MATRIX)(MatA)
• 

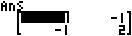
Voorbeeld 7: Om die absolute waarde van elke element van MatB te verkry (Abs(MatB)).

• (Abs)(MATRIX)(MatB)
• 

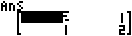
Voorbeeld 8: Bepaal die kwadraat en derde mag van MatA (MatA2, MatA3).

Neem kennis: kan nie vir hierdie insleuteling gebruik word nie. Gebruik om kwadraat te spesifiseer en (x3) om derde graad te spesifiseer.

• (MATRIX)(MatA)
• 

• (MATRIX)(MatA)(x3)
• 

Voorbeeld 9: Om die MatA = -rytrapvorm te bepaal.

• (MATRIX)(Ref)
  (MATRIX)(MatA)
• 

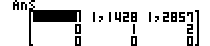
Voorbeeld 10: Bepaal die MatA = verminderde rytrapvorm.

• (MATRIX)(Rref)
  (MATRIX)(MatA)
•