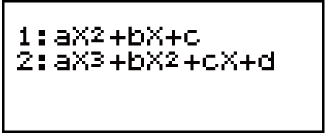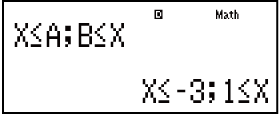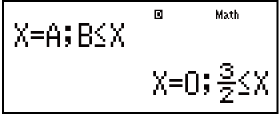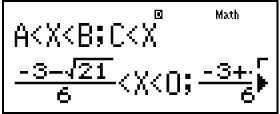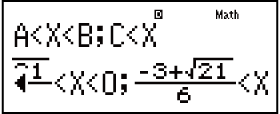Ongelykheidsberekeninge (INEQ)
Die volgende prosedure kan gebruik word om 'n kwadratiese ongelykheid of 'n derdegraadse ongelykheid op te los.
1. Druk 
(INEQ) om na die INEQ-modus te verander.
2. Op die keuselys wat verskyn, selekteer 'n ongelykheidstipe.
| Om hierdie tipe ongelykheidstipe te selekteer: | Druk hierdie sleutel: |
|---|---|
| Kwadratiese ongelykheid |  (aX2 + bX + c) |
| Kubieke ongelykheid | (aX3 + bX2 + cX + d) |
3. Op die keuselys wat verskyn, gebruik die sleutels tot 
om die ongelykheidsteken-tipe en -oriëntasie te selekteer.
4. Gebruik die koëffisiëntredigeerder wat verskyn, om koëffisiëntwaardes in te sleutel.
Om byvoorbeeld x2 + 2x - 3 < 0 op te los, sleutel die koëffisiënte a = 1, b = 2, c = -3 in deur 1
2
3 te druk.
Om 'n koëffisiëntwaarde wat reeds ingesleutel is, te verander, beweeg die wyser na die betrokke sel, sleutel die nuwe waarde in, en druk dan .
Wanneer 
gedruk word, sal dit al die koëffisiënte na nul verander.
Neem kennis: Die volgende operasies werk nie in die koëffisiëntredigeerder nie: 
, 
(M-), 
(STO). Pol, Rec, ÷R en multistellings kan ook nie met die koëffisiëntredigeerder ingesleutel word nie.
5. Nadat alle verlangde waardes is soos verlang, druk .
Dit sal die oplossings vertoon.
Om na die koëffisiëntredigeerder terug te gaan terwyl oplossings vertoon word, druk .
Neem kennis
Waardes kan nie op die oplossingskerm na ingenieursnotasie omgeskakel word nie.
Om die ongelykheidstipe te verander
Druk (INEQ) en selekteer dan 'n ongelykheidstipe in die keuselys wat verskyn. Om die ongelykheidstipe te verander, veroorsaak dat die waardes van alle koëffisiënte in die koëffisiëntredigeerder na nul verander.
Voorbeelde van INEQ-modus-berekeninge
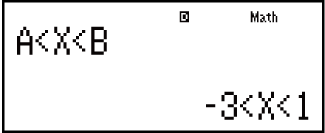
Voorbeeld 1: x2 + 2x - 3 < 0 (MthIO-MathO)
- (INEQ)(aX2 + bX + c)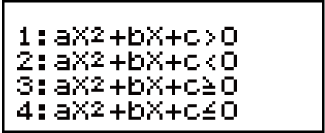
- (aX2 + bX + c < 0)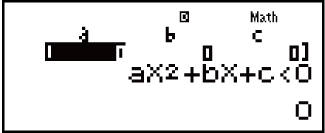
- 123
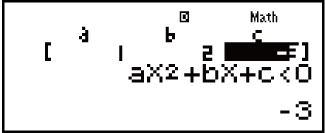
Voorbeeld 2: x2 + 2x - 3 ≧ 0 (MthIO-MathO)
- (INEQ)(aX2 + bX + c)
(aX2 + bX + c ≧ 0)
123 
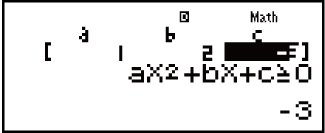
- Neem kennis: Oplossings word vertoon soos hier vertoon wanneer lineêre vertoon geselekteer is
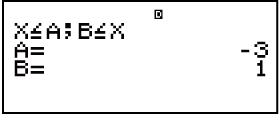
Voorbeeld 3: 2x3 - 3x2 ≧ 0 (MthIO-MathO)
- (INEQ)(aX3 + bX2 + cX + d)
(aX3 + bX2 + cX + d ≧ 0)
23 
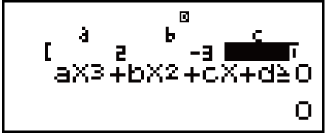
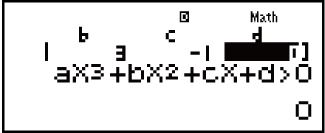
Voorbeeld 4: 3x3 + 3x2 - x > 0 (MthIO-MathO)
- (INEQ)(aX3 + bX2 + cX + d)
(aX3 + bX2 + cX + d > 0)
331 
- Neem kennis: Oplossings word vertoon soos hier vertoon wanneer lineêre vertoon geselekteer is.
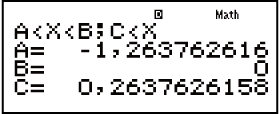
Skerm vir spesiale oplossing
"All Real Numbers" verskyn op die oplossingskerm wanneer die oplossing van 'n ongelykheid alle getalle is.
Voorbeeld: x2 ≧ 0 (MthIO-MathO)
- (INEQ)(aX2 + bX + c)
(aX2 + bX + c ≧ 0)
100 
"No-Solution" verskyn op die oplossingskerm wanneer geen oplossing vir 'n ongelykheid bestaan nie (bv. X2 < 0).
