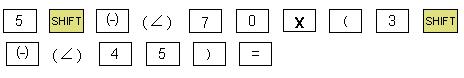Yes. At the following model,the arithmetic operations on complex numbers can be easily managed using the Calculators.
The models: fx-991MS / fx-115MS / fx-912MS / fx-3650P / fx-3950P
These kinds of calculations, which are used often in physical and technical fields, are explained here as a supplement to the calculator manual.
The complex numbers can be represented in two different forms:
Rectangular or Cartesian form: z = x+iy (In some notation j may be used instead of i.)
Polar or Phasor form: z = r∠θ or z = |z|e^θi. (In some notations φ may be used instead of θ.)
Example 1: Convert the complex number (z = -4+3i) into polar form.
1. In the COMPLEX Mode, set the angle unit to Degree (Deg).
[MODE] [2](COMPLEX)
[MODE]...[1](Deg)
2. Input the complex numbers z=-4+3i.
[(-)][4][+][3][ENG](i)[=]
3. The result in rectangular form.
The value of real part: -4
The value of imaginary part after pressing [SHIFT][=] (Re<->Im): 3 (i)
4. The display change of the value of rectangular form is carried out at polar form.
The absolute value of the number in polar form after pressing [SHFT][+](>r∠θ)[=]: 5
The angle value after pressing [SHFT][=] (Re<->Im): 143.1301024
The result in polar form :5∠143.1301024 (Angle unit:Deg)
Example2: Convert the complex number (2∠60゜) into rectangular form.
1. In the COMPLEX Mode, set the angle unit to Degree (Deg).
[MODE] [2](COMPLEX)
[MODE]...[1](Deg)
2. Input the complex numbers 2∠60.
[2][SHIFT][(-)](∠)[6][0][=]
3. The result in rectangular form.
The value of real part: 1
The value of imaginary part after pressing [SHIFT][=] (Re<->Im): 1.732050808 (i)
The result in rectangular form: 1+1.732050808i
It is possible to work with the angle unit Radian. When angle mode is set as Radian, the angle values can input as pi-Multipliers. (180゜ =π radian.)
Above Example2 is calculated in Radian.
1. In the COMPLEX Mode, set the angle unit to Radian(Rad).
[MODE][2](COMPLEX)
[MODE]...[2](Rad)
2.Input the complex numbers 2∠π/3. (60゜=π/3 radian.)
[2][SHIFT][(-)](∠)[SHIFT] [EXP](π)[ab/c] [3][=]
3. The result in rectangular form.
The value of real part: 1
The value of imaginary part after pressing [SHIFT][=] (Re<->Im): 1.732050808 (i)
Complex Numbers – Calculation (Addition / Subtraction)
The two rectangular form complex numbers z1 and z2 are given. :
z1 = 4+2i, z2 = -1+5i
Example 3: Addition z1+z2=3+7i
1. In the COMPLEX Mode, set the angle unit to Degree (Deg).
[MODE] [2](COMPLEX)
[MODE]...[1](Deg)
2. Input the value. z1+z2. |
 |
Displayed Result:
The value of real part: 3
The value of imaginary part after pressing [SHIFT] [=](Re<->Im): 7 (i)
Example4: Subtraction z1-z2=5-3i
1. In the COMPLEX Mode, set the angle unit to Degree (Deg).
[MODE] [2](COMPLEX)
[MODE]...[1](Deg)
2. Input the value. z1-z2. |
 |
Displayed Result:
The value of real part: 5
The value of imaginary part after pressing [SHIFT] [=](Re<->Im): -3 (i)
Complex Number – Calculation (Multiplication / Division)
The two polar form complex numbers z1 and z2 are given.(Angle unit:Degree):
z1 =5∠70, z2 = 3∠45
Example 5: Multiplication z1*z2=15∠115
1. Set the complex mode, the polar form for display of complex number calculation results and the angle unit Degree in setting.
[MODE][2](COMPLEX)
[MODE]...[1](Disp)[right cursor key][2](r∠θ)
[MODE]...[1](Deg)
2.Input the value. z1*z2 |
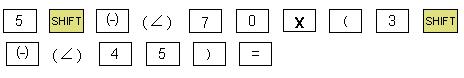 |
Displayed Result:
The absolute value of the number in polar form : 15
The angle value after pressing [SHFT][=] (Re<->Im): 115
Example6: Division z1/z2= 1.666666667∠ 25
1. Set the complex mode, the polar form for display of complex number calculation results and the angle unit Degree in setting.
[MODE][2](COMPLEX)
[MODE]...[1](Disp)[right cursor key][2](r∠θ)
[MODE]...[1](Deg)
2.Input the value. z1/z2 |
 |
Displayed Result:
The absolute value of the number in polar form : 1.666666667
The angle value after pressing [SHFT][=] (Re<->Im): 25
3.The display change of the value of polar form is carried out at rectangular form.
The value of real part after pressing [SHIFT][-](>a+bi)[=]: 1.510512978
The value of imaginary part after pressing [SHIFT][=](Re<->Im): 0.704363769 (i) |